黏性介质薄砂层时频特征响应分析

范宇婷

( 1. 中国科学院 地质与地球物理研究所，北京 100029； 2. 中国海洋石油总公司 信息化部，北京 100010 )



黏性介质薄砂层时频特征响应分析

范宇婷1,2

( 1. 中国科学院 地质与地球物理研究所，北京 100029； 2. 中国海洋石油总公司 信息化部，北京 100010 )

地下介质并不是理想的弹性介质，地层存在黏性吸收作用，对地震子波的频带及峰值频率等参数产生影响.基于波场延拓理论，采用波动方程正演模拟方法，对3种不同黏性吸收程度及厚度的薄砂层进行正演模拟；采用广义S变换，分析反射复合波的瞬时频谱.结果表明：薄砂层瞬时频谱的峰值频率与无黏性吸收作用下相比大幅度变化，导致由峰值频率预测薄砂层厚度出现较大误差.陷频频率受地层黏性吸收作用比较小，相对比较稳定.利用陷频频率出现的周期性与薄砂层厚度之间的关系预测薄砂层厚度，可以为复杂地质环境下有利薄储层的定性识别和厚度定量预测提供支持.

黏性吸收； 薄砂层； 正演模拟； 瞬时频谱； 广义S变换

0 引言

地下介质既有弹性又存在黏滞性[1]，地震波在传播过程中存在黏性吸收作用，导致地震波高频能量衰减，地震波的峰值频率降低，谱宽变窄[2-3].Yuan Chunfang、Richer N H等以Kelvin-Voigt模型[4]和Maxwell模型[5]为基础，提出基本黏弹性介质理论[6-7].杨仁虎等指出地震波在地下介质传播过程中，存在高频能量的吸收与衰减[8].黏性吸收作用是地层固有存在的特性，因此在地震波场模拟及偏移成像处理中，必须考虑地层的黏性吸收作用，才能更好地研究地震波在地下介质中各类传播现象[9].王小杰等研究地震波在黏弹性介质中的传播与反射特征[10]，得出在黏弹性介质中需对地层加入品质因子，再计算反射系数，才更接近真实地下介质.

目前，人们[11-12]应用褶积模型，考虑震源子波频谱特征和反射系数谱变化规律两种方式，研究薄砂层地震响应特性，分析震源子波类型、频率、相位和谱宽等特性对薄砂层地震响应特征的影响，以及不同厚度薄砂层反射系数谱的变化规律，给出峰值频率或陷频频率与薄砂层厚度之间的定量关系[13-18].薄砂层正演模拟方法由时域褶积方法向波动方程方面转变[19]，使模拟后的波场信息更加丰富、更加接近采集实际.薄砂层分析由傅里叶变换向广义S变换[20]和匹配追踪[21-23]等先进时频分析方法方向转变，注重反射波频谱的瞬时特性，预测方法也由定性转向定量[24].

薄砂层的正演模拟和解释识别是建立在地层为弹性介质假设基础上的，忽略地层的黏性吸收作用，现有的方法无法适用于实际的地震资料解释，主要存在问题：首先，黏性吸收使反射波的振幅随着传播时间的增加而逐渐降低，使得利用振幅定量预测薄砂层厚度的一类方法出现较大误差.其次，黏性吸收作用的频散作用使地震子波产生时变扭曲，导致地震波的走时出现误差.由于地震子波高频成分存在损失，导致地震子波的波形变胖，造成薄砂层的视厚度的定性判断出现较大误差.再次，黏性吸收作用导致地震子波的频带宽度变窄，峰值频率向低频移动，使得以频率方法为主的薄砂层厚度定量预测出现较大误差.因此，有必要研究在黏性吸收作用下薄砂层时频响应特征变化规律，寻找对黏性吸收参数变化不敏感的参数，以更好地指导薄砂层的定性解释和厚度的定量预测.

根据波场延拓理论，采用波动方程正演模拟方法，利用3种不同黏性吸收程度的黏性介质，对不同厚度的薄砂层进行波动方程正演模拟，从获取炮记录中抽取零偏移距地震道；利用时频分析方法得到反射复合波的瞬时频谱，考察不同厚度、不同黏性吸收程度薄砂层的时频特征变化规律；从频域振幅谱、峰值频率、陷频频率，以及时域波形、振幅、视厚度中优选对黏性吸收参数敏感的属性特征参数，为黏性吸收介质薄储层的定性识别和厚度的定量预测提供指导.

1 正演模拟方法

采用波动方程相移正演方法对薄砂层进行正演模拟.设震源子波的频谱为f(ω)，在黏性吸收介质条件下，各水平界面处的地震波正传波场为

P′(kx,zi,ω)=f(ω)e-jkzizi,

(1)

式中：P′(kx,zi,ω)为地震波的正传波场；j为虚数单位；zi为第i个反射界面所在的深度；kzi为垂直方向上的波数，可表示为

(2)

式中：ci为第i层的地震波传播速度；Qi为第i层的品质因子，表征地层的黏性吸收特性的强弱；kx为水平波数.

当地震波传播到最深界面处时，经过界面反射后从z=zi传播到z=zi-1处的反传波场，与z=zi-1处产生的反射波场迭加得到z=zi-1处的总反射波场：

P″(kx,zi-1,ω)=P″(kx,zi,ω)e-j(zi-zi-1)kzi+P′(kx,zi-1,ω)Rzi-1.

(3)

将迭加后的波场P″(kx,zi-1,ω)作为下一界面处延拓的初始值，依次迭代逐步向上延拓，直到延拓到地面被各接收点所接收，形成地面反射波场，记为P″(kx,0,ω)，将地面波场作反傅里叶变换：

(4)

式中：P(x,t)为薄砂层的地震正演数据.

2 地质模型及数值模拟

建立黏性吸收介质薄砂层地质模型(见图1).该地质模型由上下均匀背景泥岩和中间薄砂层组成，其中薄砂层顶界的反射因数设为-0.5，薄砂层底界的反射因数设为0.5.整个介质模型的速度为2 000 m/s；设定上下背景泥岩的厚度，使薄砂层的中心位于2 ms位置；为了研究方便，无论是背景泥岩还是薄砂层砂岩，设定相同的品质因子.按照黏性吸收程度的不同，分别考虑强吸收(Q=66)、中等吸收(Q=100)和弱吸收(Q=200)条件，考察不同黏性吸收程度对薄砂层时频特性的影响；地震子波采用峰值频率为30 Hz零相位雷克子波；采用波动方程正演模拟获取炮集数据；采取中间放炮、两边接收的采集方式，检波器之间距离设为10 m；每个炮集共包含1 000道数据；地震道采样点个数为2 000，采样间隔为2 ms.薄砂层厚度以2 m为间隔从1 m变化到29 m，3种黏性吸收条件共模拟45套地震数据体.

图1 黏性吸收薄砂层地层模型Fig.1 The thin layer model in viscous absorption media

从炮集中抽取零偏移距地震道，分别读取时域最大振幅和薄砂层的视厚度(当顶底反射因数相反时，分别读取薄砂层界面处反射子波的峰、谷对应的时刻).采用广义S变换对该地震道进行时频变换，在时频分析图上薄砂层对应2 ms位置处，获取薄砂层反射波的瞬时频谱，并计算瞬时振幅谱；从瞬时振幅谱分别读出峰值频率、陷频频率及峰值频率的振幅幅度，统计分析45套时频分析数据；考察不同黏性吸收条件下不同厚度薄砂层的时频域特征的变化规律.

3 数据分析

3.1 峰值频率

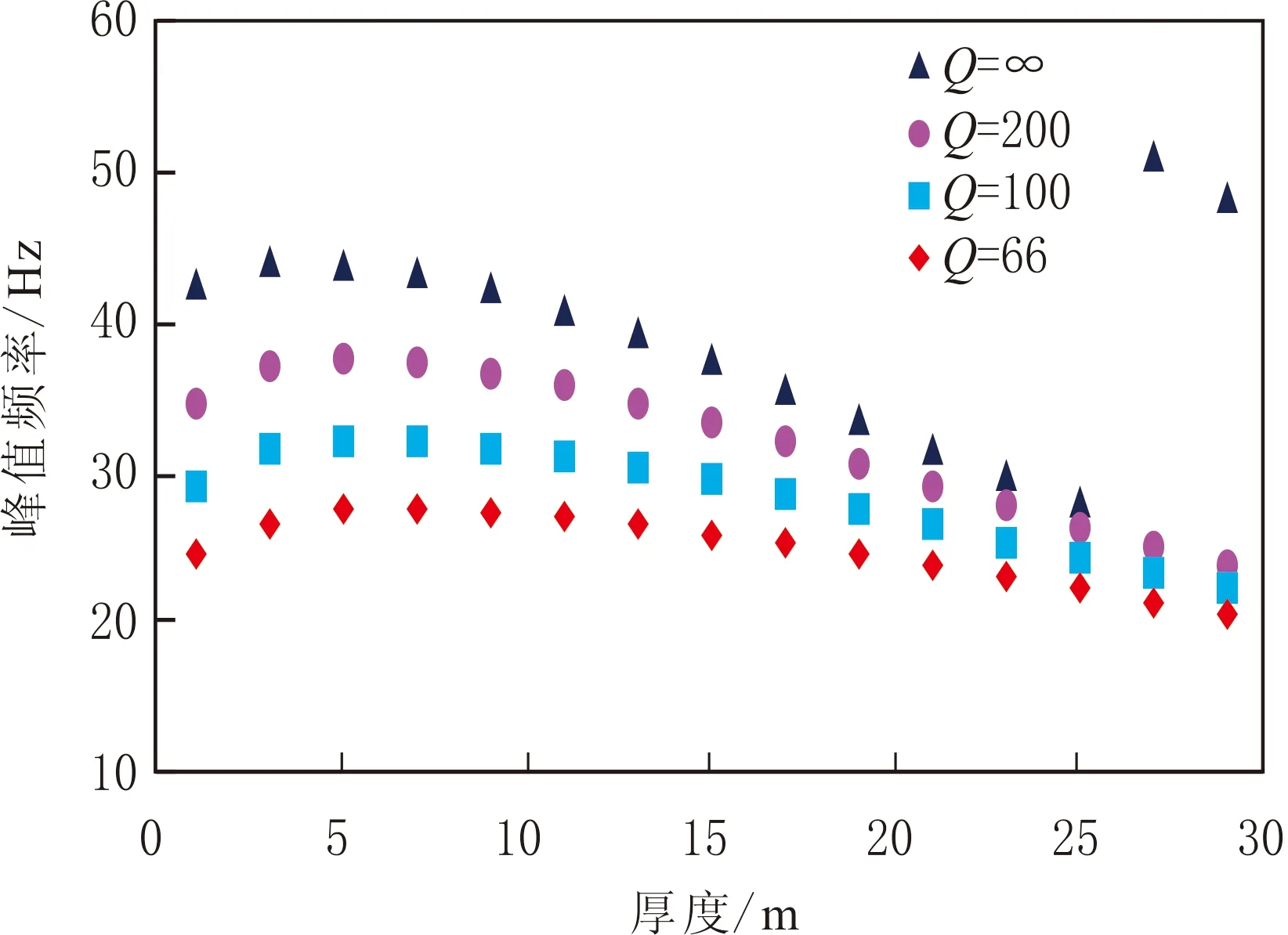
图2 峰值频率随薄砂层厚度变化关系Fig.2 The crossplot for peak frequency versus thickness of thin layer

在不同黏性吸收条件下，薄砂层峰值频率总体变化规律：在Q不变条件下，随着薄砂层厚度的减薄(大于5 m)，峰值频率逐渐增大(见图2)；当薄砂层厚度小于5 m时，峰值频率随着薄砂层厚度的减薄而逐渐减小；总体变化规律与无黏性吸收地层的类似.当Q逐渐减小时，峰值频率逐渐降低，并且地层越薄，降低的幅度越大.这说明在黏性吸收条件下，瞬时频谱的峰值频率向低频方向移动；在无黏性吸收条件下，当薄砂层厚度等于1/2波长时，峰值频率发生跃变，由低频峰转变为高频峰.在黏性吸收条件下，高频能量被相对大幅度衰减，使得瞬时频谱中并不存在高频峰，峰值频率并不发生跃变，随着薄砂层厚度的增加而逐渐降低.在给出Q条件下，地层厚度越大时，不同Q之间与无黏性地层相比，最小频率差为6 Hz(地层厚度为25 m)，最大峰值频率差为18 Hz(地层厚度为1 m)，说明在薄砂层(小于1/4波长)条件下黏性吸收大幅改变峰值频率，从而使由峰值频率预测薄砂层厚度出现较大的误差.

3.2 瞬时频谱最大幅度

在不同黏性吸收条件下，峰值频率幅度的总体变化规律：随着薄砂层厚度的减薄，瞬时频谱的峰值频率幅度先增大后减小，总体趋势与无黏性吸收地层的一致(见图3).在黏性吸收条件下，并不是像无黏性吸收地层一样在1/4波长处取得最大值，在1/2波长处取得极小值，而是极大值点向薄砂层增厚方向移动.峰值频率幅度随着Q减小而逐渐降低，其极大值所对应薄砂层厚度逐渐增大(当Q=200时，为15 m；当Q=100时，为17 m；当Q=66时，为21 m；当无黏性吸收时，为13 m，在1/4波长处)，到达幅度极大值后，幅度随薄砂层厚度变化逐渐趋于平缓.

3.3 陷频频率

在不同黏性吸收条件下，陷频频率随薄砂层厚度变化的总体规律：在存在与不存在黏性吸收条件下薄砂层陷频频率近似相等，总体上随着薄砂层厚度减薄，陷频频率有逐渐增大的趋势(见图4).一般薄砂层瞬时频谱只存在单一陷频点，但是在不同Q的瞬时频谱中可以看到只有少数薄砂层厚度存在陷频点.当Q为200时，19 m以上地层存在陷频点；当Q为100时，21 m以上地层存在陷频点；当Q为66时，23 m以上地层存在陷频点.在无黏性吸收条件下，15 m以上地层存在陷频点.随着Q的减小，具有陷频点的薄砂层数量减少，主要原因是位于陷频点右侧的高频峰易于受到强烈的高频衰减，当衰减到一定程度时，高频峰的能量全部损失殆尽，在瞬时频谱上表现为无明显陷频频率点.

薄砂层频谱属于周期性频谱，陷频频率位置呈周期性分布，并且相邻两个陷频频率差是薄层时间厚度的倒数[25]，即

Pf=fn-fn-1=1/τ,

(5)

式中：Pf为陷频周期；fn为第n个陷频频率；τ为薄层的时间厚度.

由图4可知，地层的黏性吸收作用对薄砂层的陷频频率影响较小，且当薄砂层厚度大于15 m时，陷频频率与地层厚度呈反比关系，因此，当地层存在黏性吸收时，可以利用陷频频率预测地层厚度，其精确程度好于峰值频率的.

3.4 瞬时谱宽

定义振幅谱最大幅度的10%对应的频率差为薄砂层局部频谱的瞬时谱宽.当地层无黏性吸收(Q=∞)时，瞬时谱宽的变化规律：当薄砂层厚度大于1/2波长时，瞬时谱宽随着薄砂层厚度减薄逐渐增大，瞬时谱宽为高频峰的瞬时谱宽；当薄砂层厚度不大于1/2波长时，随着薄砂层厚度的减薄，瞬时谱宽逐渐增宽；在地层厚度为1 m时略有减小，瞬时谱宽为低频峰的谱宽.

图3 瞬时频谱最大幅度随薄砂层厚度变化关系Fig.3 The crossplot for maximum amplitude of frequency spectrum versus thickness of thin layer

图4 瞬时频谱陷频频率随薄砂层厚度变化关系Fig.4 The notched frequency of instantaneous amplitude spectrum versus thickness of thin layer

图5 瞬时谱宽随薄砂层厚度变化关系Fig.5 The bandwidth of spectrum vary with single layer thickness

当地层存在黏性吸收时，由于高频峰具有强烈衰减作用，瞬时频谱只存在低频峰，因此瞬时谱宽基本上为低频峰的谱宽(见图5)，并且瞬时谱宽随着薄砂层厚度的减薄而逐渐增宽.高Q值增宽的幅度较迅速，低Q值增宽的幅度较缓.当地层厚度小于15 m时，相同地层厚度的谱宽在Q为无穷大时最宽，在Q为66时谱宽最小；在地层厚度为15～23 m条件下，在Q为200时，频谱最宽，无黏性吸收时谱宽最小；其他Q值介于两者之间.当地层厚度大于23 m时，在Q为66时，瞬时谱宽最宽；在Q为200时，瞬时谱宽最小.

3.5 时域最大振幅及视厚度

不同Q对地震波的走时产生一定的影响，进而影响由峰谷走时计算的视厚度.以1/4波长为界，当薄砂层厚度小于1/4波长时，由峰谷对应走时计算的视厚度大于薄砂层的真实厚度，且Q越小，偏差越大；地层厚度为15～19 m时，由Q为66计算的走时大于理论值，其他的小于理论值；当地层厚度大于19 m时，所有由Q计算的视厚度小于理论值.由Q为66与200计算的视厚度更接近于理论值(见图6).

反射复合波时域最大振幅随薄砂层厚度变化的基本趋势是一致的(见图7)，即最大振幅先随薄砂层厚度的减薄，振幅先增大；在达到最大值后，随薄砂层厚度的减小而减小.时域最大振幅受Q影响较大，Q越小，时域振幅越小，且最大值并不在1/4波长处取得，而是向薄砂层厚度增大方向偏移.

图6 薄砂层的视厚度随实际厚度变化关系Fig.6 The comparison between apparent thickness and the true thickness of thin layer

图7 时域最大振幅随薄砂层厚度变化关系Fig.7 The maximum amplitude in time-domain versus thickness of thin layer

4 讨论

谱宽与瞬时频谱的峰值频率幅度密切相关.当薄砂层厚度小于1/4波长时，薄砂层具有升频降幅的作用[26]，瞬时频谱的峰值幅度是逐渐降低的，且频谱的最大幅度变化率是比较平缓的.因此，瞬时谱宽是测量瞬时频谱的基部，幅度越小，测量的谱宽越接近基部，谱宽越大.当地层存在黏性吸收时，随黏性吸收作用的增强，高频能量全部损失殆尽，因此频谱宽度逐渐减小.当薄砂层厚度大于1/4波长时，瞬时频谱的幅度随着地层厚度的增加先减小后趋于稳定，因此频谱宽度变化不大.当薄砂层厚度大于1/2波长时，由于陷频频率存在，导致一部分高频能量得以增强，使得谱宽随着Q的减小进一步增强.

根据正演模拟结果，薄砂层的频率特征参数受地层黏性吸收作用影响较大，基于频率参数的薄砂层厚度预测方法将受到不同程度的影响.因此，在进行薄砂层厚度预测前，应对采集到的地面地震资料进行黏性吸收补偿叠前时间偏移成像处理[27]，才能正确补偿地层的黏性吸收作用，从而降低由变化后的峰值频率预测薄砂层厚度所带来的误差.

此外，在黏性介质传播过程中，地震波将根据地层吸收特性的强弱，出现不同程度的频散，使得不同频率的地震波以不同的速度进行传播，导致地震波的走时发生变化，使得由峰谷走时方法预测薄砂层视厚度出现较大的偏差.

5 结论

(1)将品质因子引入到波动方程正演模拟中，在波场延拓中考虑地层的黏性吸收特性的影响，使正演模拟得到的薄砂层时频响应规律更加接近地下实际.

(2)地层存在黏性吸收作用，薄砂层瞬时频谱的峰值频率与无黏性吸收作用下相比大幅变化，导致由峰值频率预测薄砂层厚度出现较大误差.在进行薄砂层厚度预测前，必须进行地震资料的高分辨叠前成像处理，正确补偿地层的黏性吸收作用，才能降低由峰值频率预测薄砂层厚度的误差.

(3)由于黏性吸收作用造成频散，导致地震波的走时发生变化.由峰谷走时预测的视厚度受黏性吸收作用影响，使得测量结果与理论值出现较大的偏差.

(4)陷频频率受地层黏性吸收作用比较小，在黏性吸收条件下，可以利用陷频频率出现的周期性与薄砂层厚度的定量关系预测薄砂层厚度.

[1] 杜启振,杨慧珠.线性黏弹性各向异性介质速度频散和衰减特征研究[J].物理学报,2002,51(9):2101-2018. Du Qizhen, Yang Huizhu. Velocity dispersion and attenuation in anisotropic linear viscoelastic media [J]. Acta Physica Sinica, 2002,51(9):2101-2018.

[2] 郑鸿明,薛为平,蒋琳,等.黏弹性介质中地震波的吸收衰减补偿方法[J].新疆石油地质,2006,27(5):556-558. Zheng Hongming, Xue Weiping, Jiang Lin, et al. Compensation method of seismic wave absorption and attenuation in viscoelastic media [J]. Xinjiang Petroleum Geology, 2006,27(5):556-558.

[3] 孙成禹.地震波理论与方法[M].东营:中国石油大学出版社,2007. Sun Chengyu. Seismic wave theory and method [M]. Dongying: China University of Petroleum Press, 2007.

[4] Yuan Chunfang. Seismic wave propagating in Kelvin-Voigt homogeneous visco-elastic media [J]. Science in China: Series D Earth Sciences, 2006,49(2):147-153.

[5] Richer N H. Transient waves in visco-elastic media [M]. Amsterdam: Elsevier Scientific Pub. Co., 1977:1-278.

[6] Aki K, Richards P G. Quantitative seismology [M]. 2nd ed. Sansalito: University Science Books, 2002.

[7] 张中杰.地震各向异性研究进展[J].地球物理学进展,2002,17(2):281-293. Zhang Zhongjie. A review of the seismic anisotropy and its applications[J]. Progress in Geophysics, 2002,17(2):281-293.

[8] 杨仁虎,常旭,刘伊克,等.黏弹性介质地震波场正演数值模拟[C]∥中国地球物理.合肥:中国科学技术大学出版社,2009:428-429. Yang Renhu, Chang Xu, Liu Yike, et al. Viscoelastic wave inhomogeneous isotropic medium is speech based on numerical simulation [C]∥Geophysical Chinese. Hefei: University of Science and Technology of China Press, 2009:428-429.

[9] 范家参.黏弹性介质中的地震波[J].地震研究,2001,24(4):358-359. Fan Jiashen. Seismic waves is viscoelastic medium [J]. Journal of Seismological Reseearch, 2001,24(4):358-359.

[10] 王小杰,印兴耀,吴国忱,等.黏弹性介质地震波传播特征及反射特征研究[J].物探化探计算技术,2012,34(3):258-266. Wang Xiaojie, Yin Xingyao, Wu Guochen, et al. Study on propagation characteristics and reflection characteristics of seismic wave in viscoelastic medium [J]. Computing Techniques for Geophysical and Geochemical Exploration, 2012,34(3):258-266.

[11] 崔凤林,管叶君.时频分析——薄互层结构研究的新途径[J].石油物探,1992,31(2):1-15. Cui Fenglin, Guan Yejun. Time-Frequency analysis: A new way for tin interbeds examination [J]. Geophysical Prospecting for Petroleum, 1992,31(2):1-15.

[12] Knapp R W. Energy distribution in wavelets and implications on resolving power [J]. Geophysics, 1993,58(1):39-46.

[13] De Voogd N, den Rooijen N. Thin-layer response and spectral bandwidth [J]. Geophysics, 1983,48(1):12-18.

[14] 凌云,西晓宇,孙德胜,等.薄储层叠后反演影响因素分析与地震属性解释研究[J].石油物探,2008,47(6):531-558. Ling Yun, Xi Xiaoyu, Sun Desheng, et al. Analysis on affecting factors of post-stack inversion and seismic attribute interpretation of thin reservoir [J]. Geophysical Prospecting for Petroleum, 2008,47(6):531-558.

[15] 孙鲁平,郑晓东,首皓,等.薄层地震峰值频率与厚度关系研究[J].石油地球物理勘探,2010,45(2):254-259. Sun Luping, Zheng Xiaodong, Shou Hao, et al. The studies on relationship between thin layer seismic peak frequency and its thickness [J]. Geophysical Prospecting for Petroleum, 2010,45(2):254-259.

[16] Okaya D A. Spectral properties of the earth's contribution to seismic resolution [J]. Geophysics, 1995,60(1):244-251.

[17] Marfurt K J, Kirlin R L. Narrow-band spectral analysis and thin-bed tuning [J]. Geophysics, 2001,66(4):1274-1283.

[18] Partyka G A, Gridley J M, Lopez J. Interpretational applications of spectral decomposition in reservoir characterization [J]. The Leading Edge, 1999,18(3):353-360.

[19] 周丽,顾汉明,马灵伟,等.基于波动方程正演模拟分析薄砂层含不同流体的AVO特征[J].地质科技情报,2013,32(2):169-173. Zhou Li, Gu Hanming, Ma Lingwei, et al. Analysis of AVO characterisitics on thin sand reservoir with various fluid based seismic modeling [J]. Geological Science and Technology Information, 2013,32(2):169-173.

[20] 熊晓军,贺振华,黄德济,等.广义S变换在地震高分辨处理中的应用[J].勘探地球物理进展,2006,6(29):415-418. Xiong Xiaojun, He Zhenhua, Huang Deji, et al. Application of generalized S transform in seismic high resolution processing [J]. Progress in Exploration Geophysics, 2006,6(29):415-418.

[21] Mallat S, Zhang Z. Matching pursuits with time-frequency dictionaries [J]. IEEE Transactions on signal processing, 1993,41(12):3397-3415.

[22] 杨昊,郑晓东,李劲松,等.基于匹配追踪的薄层自动解释方法[J].石油地球物理勘探,2013,48(3):429-435. Yang Hao, Zheng Xiaodong, Li Jinsong, et al. Thin-bed automatic interpretation based on matching pursuit [J]. Geophysical Prospecting for Petroleum, 2013,48(3):429-435.

[23] 宋维琪,朱卫星,孙英杰.复数子波匹配追踪算法识别薄层砂体[J].地球物理学进展,2007,22(6):1796-1801. Song Weiqi, Zhu Weixing, Sun Yingjie. Identify bed layer sandbody by complex wavelet matching algorithm [J]. Progress in Geophysics, 2007,22(6):1796-1801.

[24] 刘震,张万选,张厚福.储层厚度定量解释方法研究[J].石油地球物理勘探,1991,26(6):777-784. Liu Zhen, Zhang Wanxuan, Zhang Houfu. A research into quantitative interpretation of reservoir thickness [J]. Geophysical Prospecting for Petroleum, 1991,26(6):777-784.

[25] 黄绪德.薄层陷频法[J].勘探地球物理进展,2002,25(5):1-6. Huang Xude. Discussion on notches in thin-bed [J]. Progress in Exploration Geophysics, 2002,25(5):1-6.

[26] 李雪英,陈树民,王建民,等.薄层时频特征的正演模拟[J].地球物理学报,2012,55(10):3410-3419. Li Xueying, Chen Shumin, Wang Jianmin, et al. Forward modeling studies on the time-frequency characteristics of thin layers [J]. Chinese Journal of Geophysics, 2012,55(10):3410-3419.

[27] 李雪英,文慧俭,张桐,等.黏性介质叠前时间偏移方法[J].东北石油大学学报,2013,37(4):98-104. Li Xueying, Wen Huijian, Zhang Tong, et al. The method of prestack time migration in anelastic media [J]. Journal of Northeast Petroleum University, 2013,37(4):98-104.

2015-04-17；编辑：任志平

国家自然科学基金创新研究群体项目(41021063)

范宇婷(1983-)，女，博士研究生，工程师，主要从事固体地球物理方面的研究.

P631

A

2095-4107(2015)03-0001-06

DOI 10.3969/j.issn.2095-4107.2015.03.001