导管架平台圆截面管柱受侧向撞击变形机理研究

李若轩， 胡志强， 阳 松

(1.上海交通大学海洋工程国家重点实验室， 上海 200240；2.中国石油天然气管道工程有限公司， 河北 廊坊 065000)



导管架平台圆截面管柱受侧向撞击变形机理研究

李若轩1， 胡志强1， 阳 松2

(1.上海交通大学海洋工程国家重点实验室， 上海 200240；2.中国石油天然气管道工程有限公司， 河北 廊坊 065000)

针对导管架平台遭受守护船侧向碰撞的场景，利用塑性力学理论和解析计算方法，分析导管架圆形截面管柱的变形机理，并推导出能量耗散的解析计算公式和预报方法。管柱的变形分为横截面方向变形和轴线方向变形，分别给出这两部分结构损伤变形能量关于撞深的解析表达式，并用LS_DYNA软件对不同参数管柱受侧向撞击的场景进行数值仿真验证，通过计算结果的对比分析，发现解析计算结果与数值仿真结果吻合良好。利用提出的方法可以快速得到管柱的变形能与撞深的关系，对导管架平台的结构设计和抗撞性研究有指导意义。

船舶碰撞；圆形截面管柱；解析计算；塑性变形能；数值仿真

0 引言

目前所应用的海洋工程平台大多是导管架平台，守护船舷侧对平台弦杆的撞击是这类平台所面临的危险之一。当守护船接近平台完成作业时，其舷侧与平台管柱发生低速碰撞，可能会对弦杆造成一定程度的结构损伤，如果损伤严重，会危及到平台的安全作业。因此，为保障导管架平台及人员的安全，在设计时需要考虑其抗撞性能。

国内外对于圆形截面管柱，在研究对象方面，集中于内部有填充材料的，或内部存在套管的管柱；在外载荷方面，多为相对两侧同时受平面径向挤压的情形。Gupta[1]等人研究了不同材料和尺寸的圆管在双向挤压下的变形特性。Niknejad[2]等人研究了有填充的圆管在双向挤压下的变形特性。Cho[3]通过模型试验和数值仿真技术，研究了管柱在低温条件下，受侧向线载荷的变形特性。Amdahl[4-8]、Wierzbicki[9]等人对圆形截面管柱受侧向撞击的场景做了实验和变形机理的研究。Amdahl研究了船体侧向垂直撞击圆形截面管柱的场景，并开展了相关实验，提出了如图1所示的变形机理模型。NORSOK规范[10]根据Amdahl的研究成果，总结出碰撞力的计算公式：

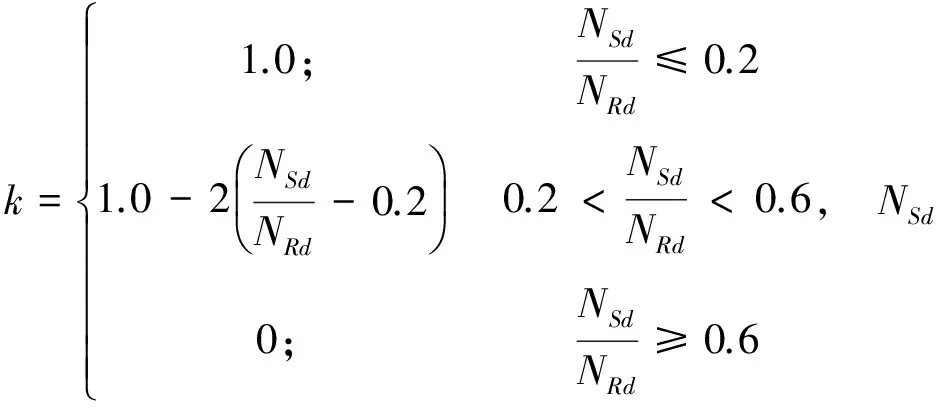
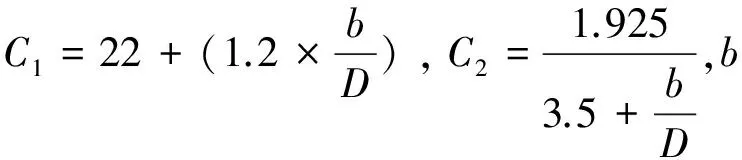
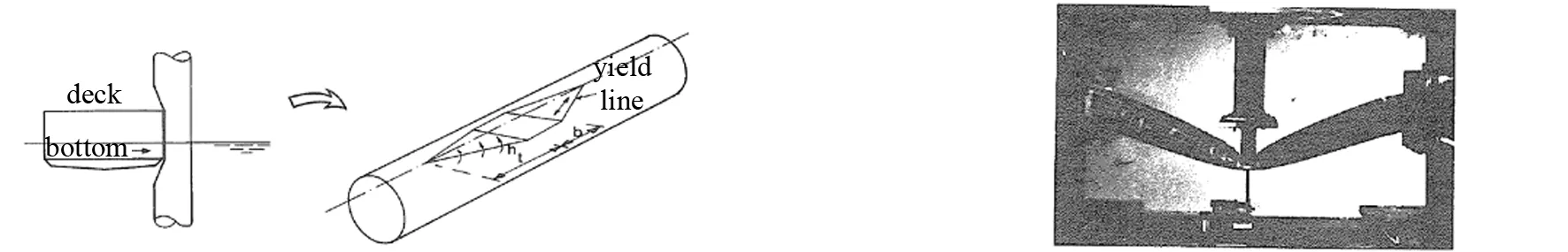
图1 Amdahl提出的变形模式及实验[4]

Wierzbicki给出了圆形截面管柱单元在遭受侧向载荷时的几何变形模式，如图2所示。能量的耗散可分为两个方向，管柱的轴线方向和横截面方向，并应用上限定理进行推导，求解出横向载荷的解析表达式：

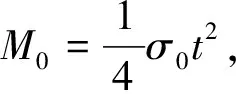
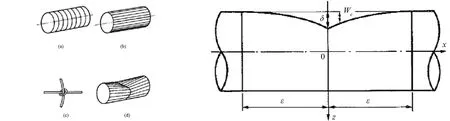
图2 Wierzbicki提出的模型

但是Amdahl和Wierzbicki的解析计算模型具有一定的局限性。Amdahl模型应用于弦杆的轴线与守护船撞击方向垂直的场景[10]，但对于深水导管架平台，出于安全性和经济性的考虑，弦杆的轴线与竖直方向存在一定的倾角，而Wierzbicki提出的解析模型是在线载荷作用下的变形模式。此外，在二者所假设的截面几何变形中，位于远离碰撞区域的一侧，截面没有产生面内的位移，实际场景中，这种位移的存在会影响管柱的整体变形和变形能吸收[10]。因此，该文针对Amdahl和Wierzbicki的不足之处开展研究。

1 解析计算模型

1.1 几何变形模式及截面变形能

该文主要讨论存在倾角的圆形截面管柱，在侧向面载荷撞击作用下的变形机理和结构变形能，变形模式如图3所示。在舷侧有横向位移时，将圆形截面管柱所发生的变形分为三个部分，分别用EⅠ、EⅡ和EⅢ表示Ⅰ、Ⅱ、Ⅲ部分的能量耗散，其方式是管柱截面的变形、材料的拉伸和结构的弯曲。此外，Ⅱ部分还存在管柱整体的旋转引起的能量吸收问题，EⅠ、EⅢ可以利用Wierzbicki的模型计算获得。该文的研究重点是II部分的能量耗散，可在两个方向上分别计算并相加得到，即横截面方向和轴线方向。

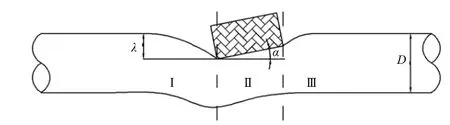
图3 圆形截面管柱结构变形侧向示意图

图4(a)为Wierzbicki提出的变形模式，该文假设的几何变形模型如图4(b)所示，即在横截面上沿撞击方向，截面存在面内的位移。这种变形模式适用于深水导管架平台遭受守护船撞击的场景中。

参照图4，在每个圆形截面上的能量耗散率：

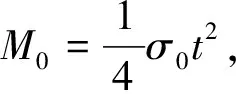
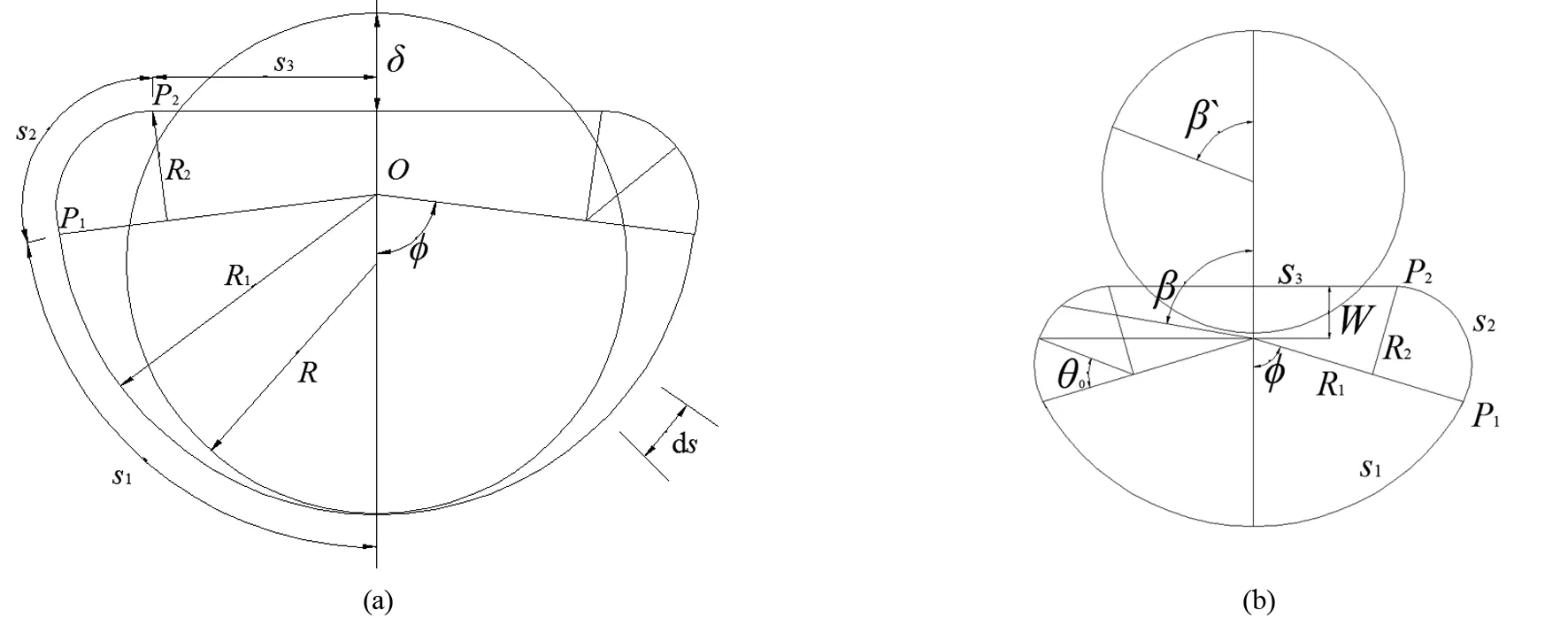
图4 圆形截面管柱截面变形图

假设变形前后截面周长不变，由于截面的对称性，只考虑半个圆形，变形后的截面由三段组成，即半径为R1的圆弧段s1、半径为R2的圆弧段s2和直线段s3，根据图4，有如下几何关系：

式中：s1=R1φ；s2=R2(π-φ)；s3=(R1-R2)sinφ；φ为圆弧段s1所对应的圆心角。

式中：V1、V2分别为塑性铰P1、P2在面内的运动速度。

此外，根据图4，还可以得出以下的几何关系：

δ=2R-[R1(1-cosφ)+R2(1+cosφ)

式(4)和式(9)是R1、R2和φ这三个未知参数关于δ的两个方程，然而尚缺少一个方程。

1.2 补充方程的提出

通过研究发现s3与δ存在着一定的几何函数关系，由于关系复杂，难以用解析方法表达，因此利用数值仿真技术，获取s3与δ之间的几何函数关系。通过数值仿真，获得截面变形模式如图5、图6所示。

图5 圆形截面管柱变形轴向视图

图6 圆形截面管柱变形侧向视图

从数值仿真计算的结果中，可以判断出舷侧位移量与截面收缩量(有效撞深)存在着函数关系[10]。

Soares[11]提出管柱结构的大变形模式，取决于L/D、D/t和载荷分布。该文假设上述两个函数关系中的参数是L/D、D/t或二者的组合形式。利用LS_DYNA软件进行数值仿真，以L/D和D/t为变量，取值范围分别为5～20和30～80，进行24个算例的计算，算例的几何参数见表1。

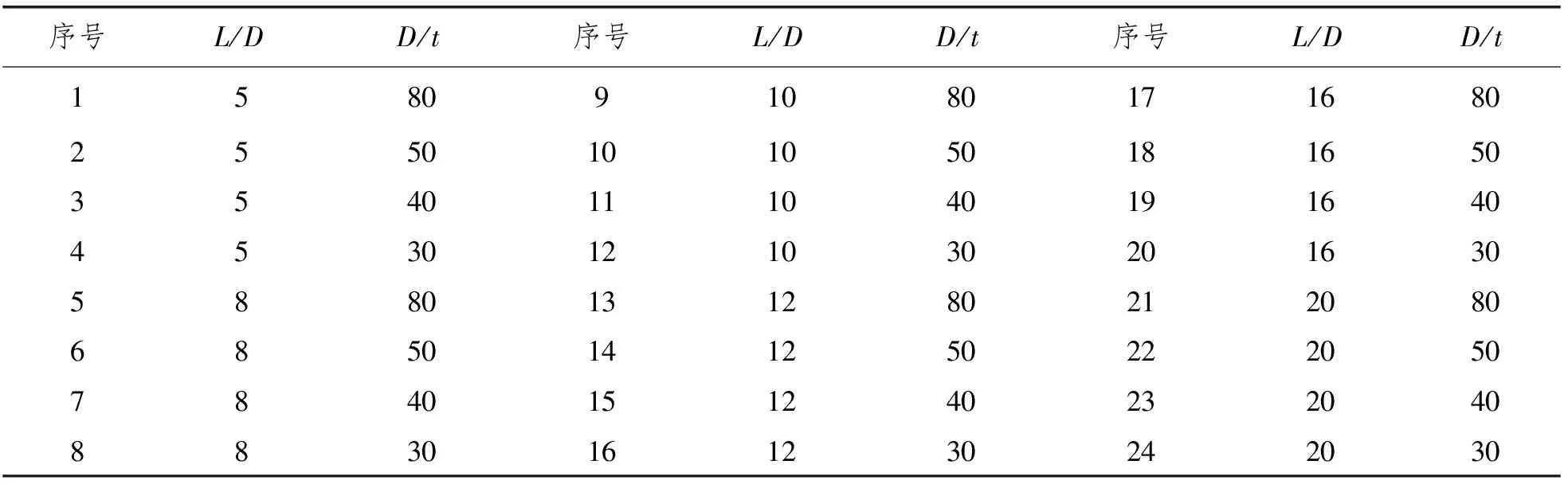
表1 算例的几何参数

根据数值计算结果，可以得到“截面收缩量—舷侧撞深”和“s3无因次长度—截面收缩率”的曲线[10]。分别对两条曲线的拟合对比，拟合结果如图7所示。

根据表1所列出所有算例的计算结果对比，可以得出下列拟合结果。

函数关系(a)为“截面收缩量—舷侧撞深”的函数关系：

函数关系(b)为“s3无因次长度—截面收缩率”的函数关系：

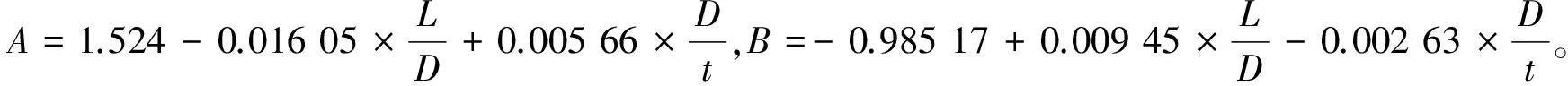
(R1-R2)sinφ

式(12)是R1、R2和φ关于δ的第三个方程，将式(4)、式(9)与式(12)联立可以得到关于φ的方程：

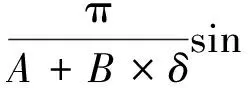
式(13)是非线性方程，可以求得任意给定撞深δ下的φ的数值解，从而通过式(8)，可以得到任意横截面上单位长度的变形能，再在轴线方向上进行积分，就可以得到Ⅱ部分横截面方向的能量。

图7 “截面收缩量—舷侧撞深”和“s3无因次长度—截面收缩率”的对比曲线

1.3 轴线方向变形能的求解

在管柱未变形时，将每一条平行于管柱轴向的线看作管柱的一个部分。轴线方向上的整体应变率为[6]：

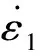
对式(15)中的3个等式，在左右两端分别进行积分，可以得到：

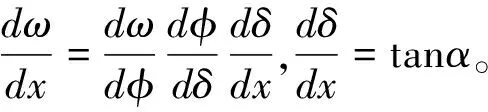
参照图4(b)，假设在整个变形过程中，截面的周向长度不变，β′角和β角分别是变形前后同一个点相对于截面中心的角度。W为变形后，截面中心到s3的垂直距离。对(16)式中的ε1、ε2和θ0分别讨论：

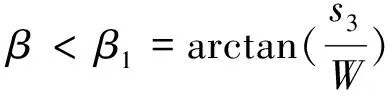
当β1<β<π-φ时，设变量ψ，其变化范围Ψ0～Ψt。

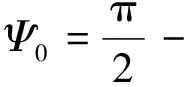
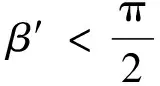
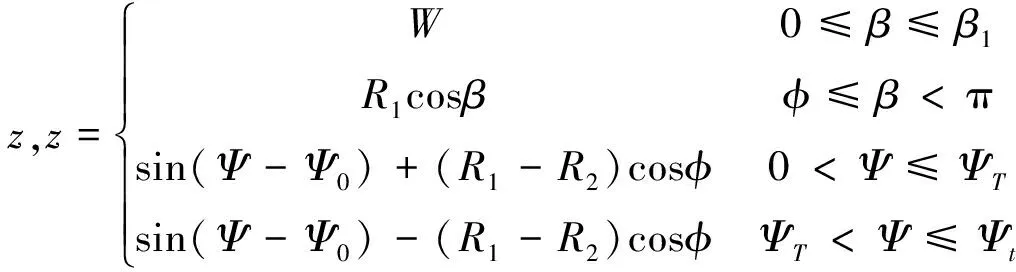
其中ΨT是使得β=90°的Ψ角值。

将上述ω与z的结果带入到式(16)中，可以通过式(17)求得在管柱轴线方向上的变形能：

式中：N0=σ0t。

1.4 总变形能的求解

在Matlab中编程，将式(17)计算得到的变形能与式(8)积分得到的变形能结果相加：

求解EⅠ和EⅢ时，可以利用Wierzbicki的解析模型，但是对应的撞深，应该是根据函数关系(a)求得的有效撞深δ，即在船侧对管柱λ的撞击位移时，管柱横截面的收缩量δ。

当δ≤Dmsinα时，

当δ>Dmsinα时，

Ⅰ、Ⅲ两部分吸收的能量

管柱所吸收的总能量E

2 数值仿真及对比验证

利用数值仿真软件LS_DYNA开展验证分析。该文不考虑重力的影响，如图8所示，建模时将管柱的轴线设为竖直方向，两端采用刚性固定。舷侧为截面如图8所示的柱体，其接触面法向量与管柱轴线夹角为α。该文关心在整个碰撞过程中圆形管柱中部的能量吸收，所以认为舷侧模型为刚体，则其可被简化为截面如图8所示的柱体，其截面是带有圆弧倒角的矩形。舷侧的运动速度为0.5m/s，接触面的摩擦系数为0.3。

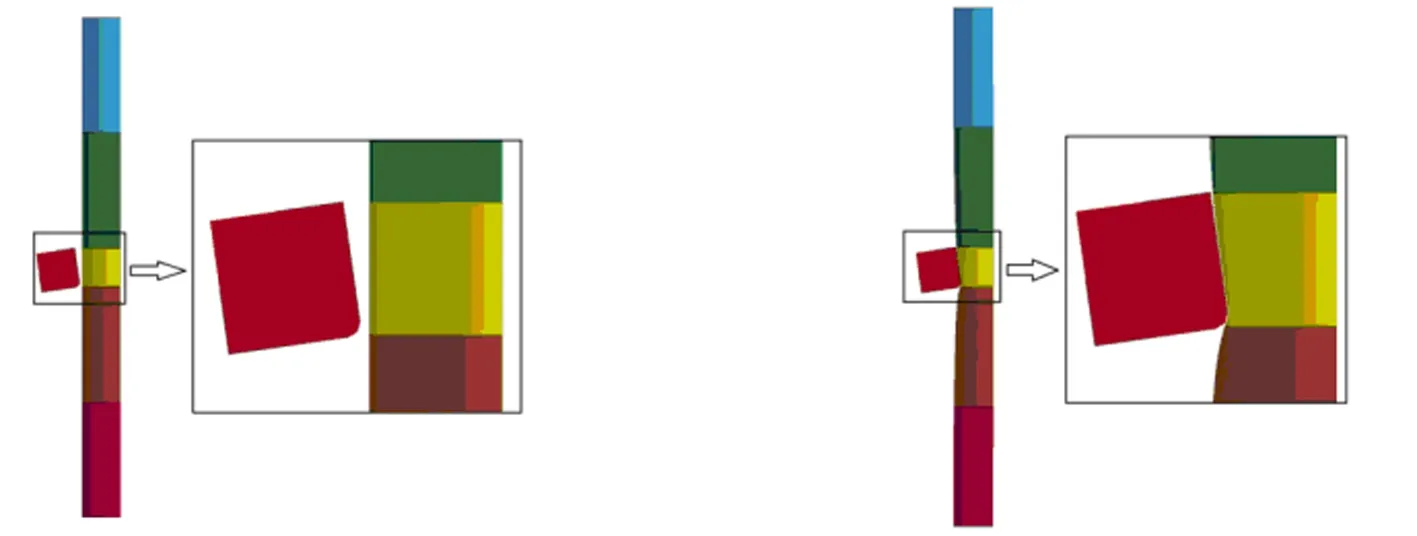
图8 LS_DYNA中碰撞前后的场景侧向示意图

分析中选取4个算例，其中模型的几何参数见表2，管柱壁厚的选取参考RenyWatan[12]的算例。

表2 模型的基本参数

计算中模型采用Belytschko-Tsay薄壳单元[13]，材料的主要力学参数见表3。

表3 材料主要力学参数

如图9所示，对比圆管中间的部分，在管柱的变形过程中，出现了薄壳单元的破裂。在撞深较小的场景下可以采用上述理论进行分析。而大变形的撞击场景下，由于管壁单元出现了撕裂破坏，导致管柱结构抗变形能力降低，所以该文所提出的变形模态不适用于大变形场景。但考虑到导管架平台与守护船碰撞场景多为低速碰撞，导管架管柱一般不会出现大幅度的结构变形。

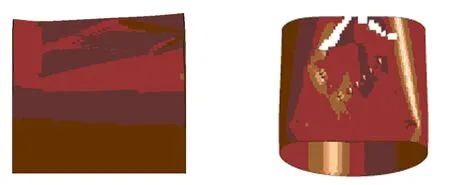
图9 LS_DYNA中的结构变形图

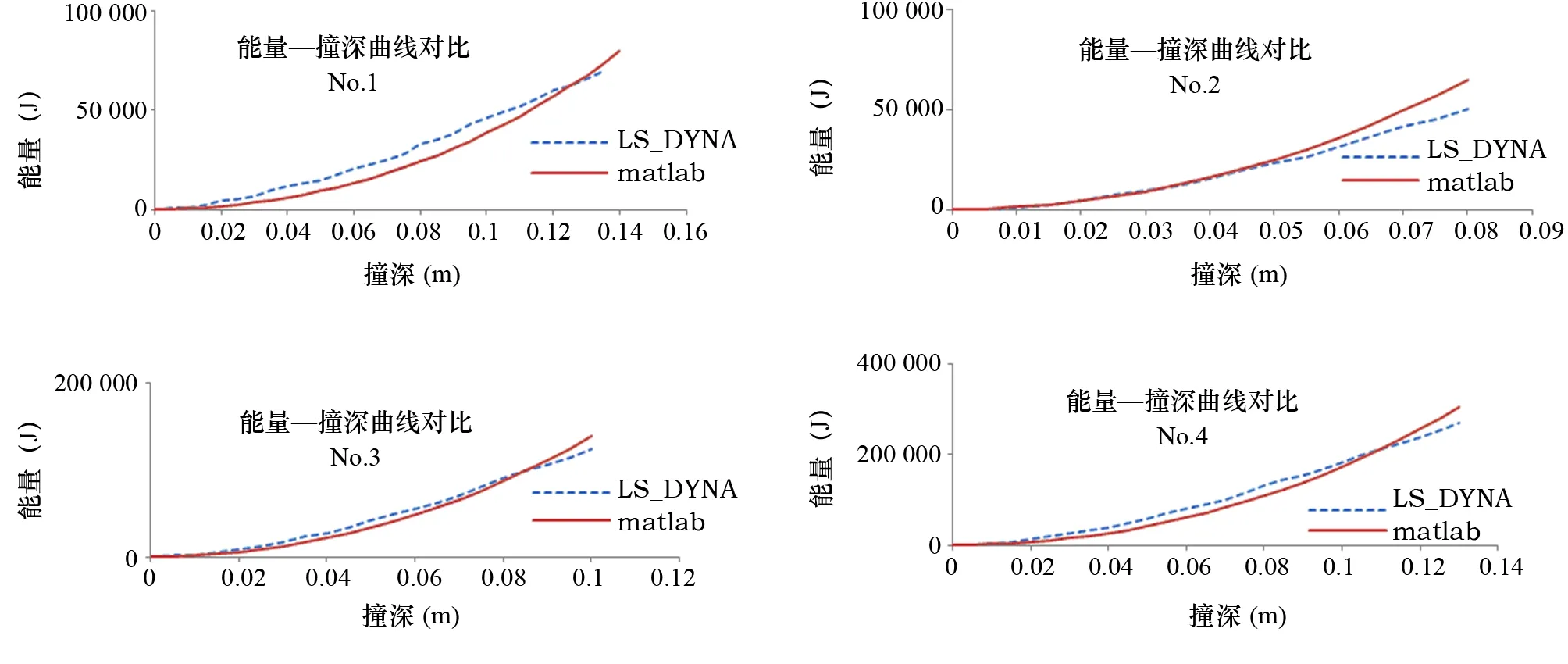
图10 解析方法与数值仿真的能量对比

如图10所示，将通过解析分析求得的变形能与通过数值仿真计算得到的结构变形能计算结果进行对比，在碰撞发生的初始阶段，解析计算的结果较数值模拟结果偏小，可能是因为舷侧于管柱的初始接触点并没有准确地存在于圆管中段的下缘。因为该处的有限元网格是过渡网格，为避免产生较大的误差，将初始接触点上移至圆管中段以内，而导致碰撞力集中于此所致。随着舷侧撞深的增加，解析计算结果较数值模拟结果偏大，其原因是有限元模型破裂，产生了单元失效，致使管柱承载能力下降，从而出现了上述结果。No.2的对比结果中，两条曲线的交点出现较早的原因可能是该工况具有较大的D/t的值。

由图10可以看出，解析方法得到的结果与数值仿真得到的结果具有令人满意的吻合度。对于存在误差的原因，可能是该文提出的解析方法暂时没有考虑管柱的两端采用刚性固定所带来的影响。随着撞深的增加，管柱单元的承载能力下降，所以出现解析计算结果较数值结果偏大的现象。

3 结论

利用数值仿真技术，对导管架平台在侧向撞击下管柱圆形截面的变形进行分析，给出更符合仿真结果的几何变形模式，以及截面中各参数关于撞深的几何函数关系。基于塑性变形理论，通过提出补充方程，使得面内几何变形的方程组可解，从而改进了Amdahl和Wierzbicki的模型和理论，提出了适用于深水导管架平台圆形截面管柱结构遭受守护船侧向撞击场景下的结构变形能解析预报方法。研究中利用数值仿真方法对模型的几何参数进行拟合，从而推导出解析计算公式。应用此方法可以得到的结构损伤变形机理和快速的解析预报方法，与数值仿真结果吻合度较好。

[ 1 ] Gupta N K, Sekhon G S, Gupta P K. Study of lateral compression of round metallic tubes[J]. Thin-walled structures, 2005, 43(6): 895-922.

[ 2 ] Niknejad A, Elahi S A, Liaghat G H. Experimental investigation on the lateral compression in the foam-filled circular tubes[J]. Materials & Design, 2012, 36(3): 24-34.

[ 3 ] Cho S R, Seo B S, Cerik B C, et al. Experimental and numerical investigations on the collision between offshore wind turbine support structures and service vessels[J]. Collision and Grounding of Ships and Offshore Structures, 2013.

[ 4 ] Amdahl J. Energy absorption in ship-platform impacts [D], Trondheim:The Norwegian Institute of Technology, 1983.

[ 5 ] Sфreide T H, Amdahl J. Deformation characteristics of tubular members with reference to impact loads from collision and dropped objects [J]. Norwegian Maritime Research, 1982, 10(2): 3-12.

[ 6 ] Sфreide T H, Moan T, Amdahl J, et al. Analysis of ship/platform impacts [J]. Behavior of Off-Shore Structures,1982, (2): 257-278.

[ 7 ] Furnes O, Amdahl J. Ship collisions with offshore platforms [J]. Intermaritec'80, 1980.

[ 8 ] Amdahl J, Eberg E. Ship collision with offshore structures [C].Structural Dynamics Eurodyn，1993.

[ 9 ] Wierzbicki T, Suh M S. Indentation of tubes under combined loading [J]. International Journal of Mechanical Sciences, 1988, 30(3): 229-248.

[10] 李若轩,胡志强.侧向撞击下导管架平台圆管杆件变形机理研究[J].《第23届全国结构工程学术会议论文集(第II册)》,2014.

[11] Soares C G, Sфreide T H. Plastic analysis of laterally loaded circular tubes[J]. Journal of Structural Engineering, 1983, 109(2): 451-467.

[12] Reny W. Analysis and Design of Columns in Offshore Structures subjected to Supply Vessel Collisions [D], Trondheim: Department of Marine Technology, NTNU, 2011.

[13] Hallquist J O. LS-DYNA theory manual [J]. Livermore Software Technology Corporation, 2006,(3)：25-31.

Research on Deformation Mechanism for Circular Section Columns of
Jacket Platform under Lateral Impact Scenario

LI Ruo-xuan1, HU Zhi-qiang1, YANG Song2

(1.State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China；2.China Petroleum Pipeline Engineering Corporation, Hebei Langfang 065000, China)

This paper proposes the mechanism of the structural damage deformation of circular section columns of a jacket platform in the scenario of being collided by a supply vessel. Based on theory of plasticity and numerical analysis, an analytical method is developed to predict the relationship between energy dissipation and indentation. The structural deformation energy of columns with different parameters in both transverse and axial directions is calculated by the proposed analytical method, which agrees well with the results obtained from numerical simulation by software LS_DYNA. The analytical method can calculate the energy dissipation rapidly, which could be meaningful to the structural design and research on crashworthiness of jacket platforms.

ship collision; circular column; analytic analysis; plastic deformation energy; numerical simulation

2014-11-06

李若轩(1989-)，男，硕士研究生。

1001-4500(2015)03-0041-08

P75

A