不规则波中动力定位半潜平台慢漂运动研究
姜宗玉, 崔 锦, 董 刚, 刘 婕
(1.挪威埃捷利海洋工程集团, 上海201206; 2.挪威船级社, 奥斯陆1363)
不规则波中动力定位半潜平台慢漂运动研究
姜宗玉1, 崔 锦1, 董 刚1, 刘 婕2
(1.挪威埃捷利海洋工程集团, 上海201206; 2.挪威船级社, 奥斯陆1363)
基于势流理论,计算了动力定位半潜式平台在不规则波中的慢漂运动响应,应用PID方法计算了平台对动力定位系统的推力需求,对比分析了海况对在纵荡、横荡及首摇三个自由度内的慢漂运动的影响。研究结果显示:平台的慢漂运动幅值与有意波高变化趋势相同,明显受漂移阻尼以及动力定位系统的影响,在各个海况下动力定位系统的需求推力极值远大于平台在该海况下承受的平均漂移力。
动力定位;慢漂运动;不规则波;漂移阻尼;半潜式平台
0 引言
半潜式平台在工作过程中,受风、浪、流等其他环境载荷的共同作用,会漂离预定位置,漂移距离超过一定范围,将产生巨大的安全隐患,因此需要限制平台的水平移动距离。动力定位是利用平台自身的动力系统抵御风、浪、流等海洋环境载荷的影响,将平台的水平移动限制在可接受范围内的一项技术。在平台所遭遇的各种环境载荷中比较复杂的是波浪载荷,波浪诱导产生的的水平运动主要包括一阶波频运动和二阶漂移运动两部分。一阶波频运动由于其可回复性以及有限的运动幅值,在多数情况下对平台的定位不产生破坏性影响,只有在浅水情况下才需要特别考虑;二阶漂移运动是动力定位系统主要抵御的运动形式,因为平均漂移力诱导平台产生定向水平运动和慢漂力诱导平台产生的大幅慢漂运动都会使平台远离其目标位置。
平台动力定位系统设计的一个很重要的方面就是对平台的动力定位能力进行分析。动力定位能力分析是指分析平台在给定环境条件下平台动力定位系统推力能否抵御环境载荷,确保平台位置保持在安全范围内。针对这一分析,API规范[1]给出了一种简化方法,此方法只考虑平台承受的平均环境载荷。孙丽萍等[2]运用这一简化方法对一艘半潜式钻井平台进行了动力定位能力分析,该分析考虑了风载荷、流载荷以及波浪平均漂移力。虽然这种简化方法简单方便,但是它没有考虑二阶慢漂力和慢漂运动,需要根据经验设定安全系数。针对这一问题,该文计算半潜式平台在三种特征海况下所承受的慢漂力以及慢漂运动,并计算了平台对动力定位系统的推力需求。计算结果显示需求推力极值远远大于平均漂移力,该方法对提高定位安全性具有实际意义。
1 理论与计算模型
该文选用笛卡尔直角坐标系作为参考坐标系,坐标原点O位于静水面,x轴指向平台艏部,y轴指向平台左舷,z轴正向竖直向上。
1.1 二阶波浪载荷
作用于浮体的水平波浪载荷可以分为一阶波浪力和二阶漂移力两部分。一阶线性波浪力幅值与波幅成正比,频率与波浪频率相等;二阶漂移力幅值与波幅的平方成正比。虽然二阶慢漂力的幅值要小于一阶波浪力,但是其周期与动力定位半潜式平台的纵荡、横荡和首摇固有周期接近,从而引起共振,导致大幅慢漂运动。
二阶漂移力可以用以下公式表达[3]:

可以看出,当j=k时,上式退化为:
其不随时间变化,即平均漂移力。在一定海况S(ω)下,波幅Aj可以由以式(3)表示:
则公式(2)可转化为积分形式:
1.2 漂移阻尼
势流理论只预报辐射阻尼,当平台运动频率降低到一定程度,辐射阻尼数值将减小到可以忽略。但实际上平台在波浪中的阻尼要大于静水中的阻尼,阻尼的增加与波浪频率和波幅有关[4],这一增加量就是漂移阻尼。
Aranha[5]提出一种近似方程用以表达规则波中的漂移阻尼系数:

1.3 动力定位控制系统
动力定位控制系统需要对输入的平台低频运动信号进行响应,目前多用PID控制器进行控制:比例增益P作为动力定位系统的刚度,微分增益D作为动力定位系统的阻尼,积分增益I可作为平台平均漂移量的补偿。整个平台的推力需求可以由下式表示:
主动脉瓣狭窄(AS)是最常见的心脏瓣膜病。其病因不尽相同,治疗上取决于AS的严重程度和患者的临床症状。随着矛盾的低血流、低跨瓣压差伴正常射血分数的重度AS的提出,重度AS的诊断和干预节点备受挑战[1] 。部分研究指出,左室纵轴收缩功能与跨瓣压差和心功能相关,因而进一步影响治疗策略与患者预后[2] ,因此本研究综合临床及超声心动图资料,对不同跨瓣压差、不同射血分数的重度AS左室纵轴收缩功能做一对比分析。
由式(7)可以看出,需求推力的大小与PID系统各系数的设置密切相关。Marin[6]对PID系数设置提出以下建议:
(1) 比例增益P根据最大可用推力和最大允许位置偏移量决定
式中:N为推进器数量;Tmax为单台推进器最大推力;Rmax为最大允许漂移量。
(2) 微分增益D根据动力定位平台的临界阻尼决定
(3) 积分增益I可以提高平均定位精度,但由于平台始终在做波频运动,设置积分增益的优点可以忽略,因此可设置为零。
1.4 浮体运动方程
式中:M为质量;A为附加质量;x为位移;B为时延函数;C为静水恢复力;F为波浪载荷;FDP为动力定位系统推进器总载荷。该文通过间接时域方法求解附体的水动力系数,首先在频域内求出附加质量系数a(ω)以及阻尼系数b(ω),然后通过快速傅立叶变换得到时域的附加质量以及时延函数。
2 半潜平台与不规则波参数
2.1 半潜平台主尺度
该文以一条动力定位半潜平台为对象,对其在不规则波中的慢漂运动进行模拟,依据挪威国家标准和DNV规范设计,主要用于北海以及挪威北部海域钻井作业。平台主尺度见表1,平台模型如图1所示。
2.2 环境参数
该文共选取3个北大西洋典型短期海况进行模拟[7],波浪谱选用P-M谱,波浪谱参数相见表2。海况SS1的特点是平均过零周期比较短且有意波高在所有短过零周期海况中相对较高;海况SS2是出现频率最高的海况;海况SS3是有意波高最大的极限海况。入射波角度设定为135°(斜浪),因为在斜浪下平台有明显的纵荡、横荡及首摇运动,可以充分反映动力定位平台的慢漂运动特性。

图1 半潜平台模型
表1 半潜式平台主尺度

名称尺度总宽(m)70.5浮筒(m)104.5×16.5×10.05立柱(m)15.5×15.5浮筒间距(m)54吃水(m)17.5排水量(t)4.04×104

表2 波浪谱
3 计算结果及分析
该文共计算了三种海况下半潜平台的慢漂运动响应。慢漂运动由平台的重心偏移量R以及首摇角度YAW表示,其中重心偏移量由以下公式定义:
式中:x1_RP与x2_RP分别为平台定位点在坐标系中的X轴和Y轴坐标。
模拟的初始状态为平台静浮在水面,速度及加速度均为零,模拟持续时间为3h,相当于短期海况的典型持续时长。
图2~图4显示的是平台在该文选取的各个海况下的二阶漂移力的计算结果。根据公式(1)可知,二阶漂移力的幅值与波幅的平方成正比。计算结果与此相符,在有意波高最大的SS3海况下的二阶漂移力最大,有意波高最小的SS2海况下的二阶漂移力最小。

图2 纵荡慢漂力
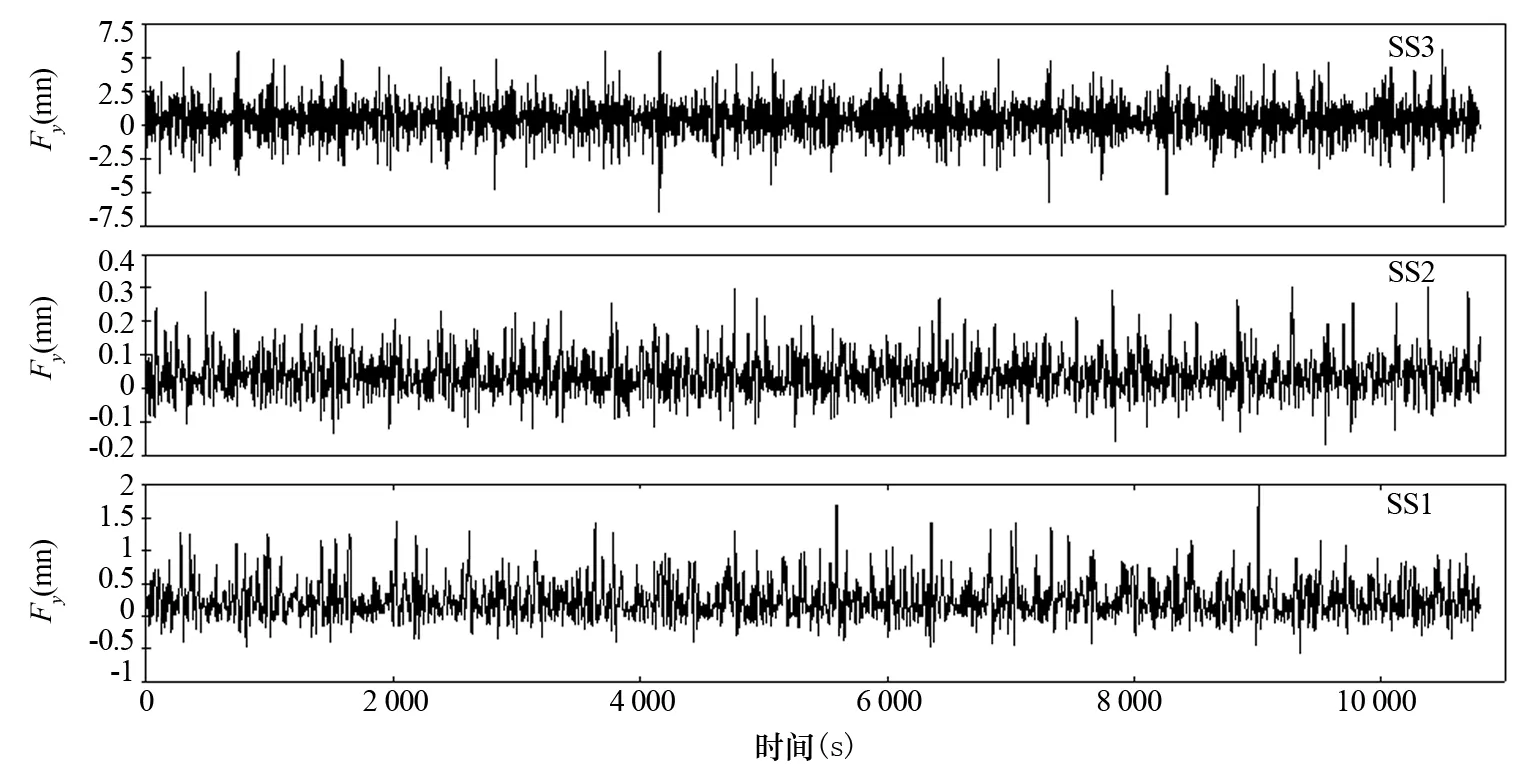
图3 横荡慢漂力

图4 首摇慢漂力矩
图5~图6显示的是平台在各个海况下的慢漂运动计算结果。二阶波浪载荷与波幅的平方成正比,较大的二阶波浪载荷导致较大的慢漂运动幅值,在较大的有意波高海况下计算的慢漂运动幅度也较大。需要注意的是各个海况下慢漂运动幅度的差别没有慢漂力的差别大,这与漂移阻尼有关,根据公式(6)可知,恶劣海况下漂移阻尼也较大,较大的漂移阻尼限制了平台的慢漂运动。限制平台慢漂运动另一个原因是动力定位系统的推力,更大幅度的运动促使定位系统产生更大的推力以限制平台运动。

图5 偏移量

图6 首摇
图7~图9显示的是在各个海况下平台对动力定位系统的推力需求的统计结果。其中:MAX代表最大值;MIN代表最小值;SD代表均方差;MEAN代表运用公式(4)计算的平均漂移力。对于一定水深,Rmax是一定的,根据式(8)、式(9)可知,比例增益和微分增益也确定,因此需求推力的幅值将由平台慢漂运动幅值和速度决定。在有意波高更高的海况下,慢漂运动幅值更大,平台对动力定位系统的推力需求也更大。均方差的幅值同样与海况的恶劣程度成正比关系,均方差反应数据相对于其平均值的离散程度,较大的均方差表明推力更加偏离其平均值,根据公式(7)可知剧烈的慢漂运动会导致需求推力的均方差增大。需要注意的是,在各个海况下,需求推力的极值要远远高于平台承受的平均漂移力,纵荡力和横荡力基本在3倍或更高,首摇力矩则为9倍或更高,因此考虑平台的慢漂运动会大大提高平台的定位安全性。

图7 纵荡需求推力 (MN) 图8 横荡需求推力(MN) 图9 首摇需求推力矩(MN·M)
4 结论
该文计算了动力定位半潜平台在不规则波中的慢漂运动以及平台对动力定位系统的推力需求。通过各个海况下计算结果的对比,分析了海况对平台慢漂运动的影响以及在不同海况下平台对动力定位系统的推力需求变化。计算结果显示,平台承受的二阶漂移力幅值主要由波幅决定,较大的漂移力会产生较大慢漂运动,平台慢漂运动明显受漂移阻尼以及动力定位系统影响。在恶劣海况下平台对动力定位系统的推力需求要远大于平台承受的平均漂移力,因此运用仅考虑平均漂移力的简化方法计算动力定位系统的定位能力,需要设定一个较大的安全系数。
[1] API recommended practice 2sk. Design and analysis of stationkeeping systems for floating structures[S].2005.
[2] 孙莉萍,刘雨,李小平. 深水半潜式钻井平台DP3动力定位能力分析[J]. 中国造船, 2011, 52(4): 100-108.
[3] Faltinsen O M. Sea loads on ships and offshore structures [M]. Cambridge: Cambridge University Press, 1990.
[4] Wichers J E W,Sluijs M F. The influence of waves on the low frequency hydrodynamic coefficients of moored vessels [C]. Proc. 11th Offshore Technology Conf., 2012.
[5] Aranha J A P. A formulation for ‘wave damping’ in the drift for a floating body [J]. J. Fluid Mech., 1994, 275:147-155.
[6] Serraris J J. Time domain analysis for DP simulations [C]. Proc. ASME 28th Int. Conf. Ocean, Offshore and Arctic Eng., 2009.
[7] DNV-RP-C205. Environmental conditions and environmental loads[S].2007.
An Investigation on Slow Drift Motions of a DP Semi-submersible Platform
JIANG Zong-yu1, CUI Jin1,DONG Gang1, LIU Jie2
(1.Agility Group (China) Ltd.,Shanghai 201206,China; 2. Det Norske Veritas, Oslo 1363, Norway)
The slow drift motions of a dynamic positioned semisubmersible in irregular waves is investigated based on potential flow theory. The required thrust of dynamic positioning system is calculated by using PID controller. A comparative research is conducted to analyze sea states’ impact to the slow drift motions in surge, sway and yaw. The research indicates that amplitude of the slow drift motions is positively proportional to the significant wave height of sea states and the amplitude is significantly influenced by drift damping and the thrust of dynamic positioning system; the maximum value of required thrust of dynamic positioning system is far higher than the mean drift force loaded on the structure at any introduced sea state.
dynamic positioning; slow drift motions; irregular waves; drift damping; semi-submersible platform
2014-08-04
姜宗玉(1981-),男,工程师 。
1001-4500(2015)03-0089-06
P751
A

