Effect of rifle bullet parameters on the penetration into ballistic gelatin

LIU Su-su(刘苏苏)， XU Cheng(徐诚)， CHEN Ai-jun(陈爱军)，LI Hong-kui(李宏魁)

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2.School of Science, Nanjing University of Science and Technology, Nanjing 210094, China; 3.Baicheng Ordnance Test Center, Baicheng 137001, China)



Effect of rifle bullet parameters on the penetration into ballistic gelatin

LIU Su-su(刘苏苏)1,， XU Cheng(徐诚)1， CHEN Ai-jun(陈爱军)2，LI Hong-kui(李宏魁)3

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2.School of Science, Nanjing University of Science and Technology, Nanjing 210094, China; 3.Baicheng Ordnance Test Center, Baicheng 137001, China)

To understand the effects of the rifle bullet parameters on the bullet-gelatin interaction quantitatively, a finite element model of bullet penetrating gelatin was set up and computational results are compared with experimental ones. The penetration of the rifle bullet into the gelatin was simulated by the nonlinear finite element method. The quantitative analysis of the changes in the gelatin interaction with the rifle bullet were conducted by changing the bullet parameters, such as attack angle on gelatin, initial velocity, warhead’s tip and location of mass center of bullet. Results demonstrate that with the increase of the attack angle, instable moment of the bullet moves forward,the length of narrow wound channel shortens,and when penetration is completed diameters of temporary cavities increase, the gelatin energy and energy transmission ratio increases; With the increase of the impact velocity, instable moment of the bullet moves forward, the maximum forces acting on the gelatin and the gelatin energy increase remarkably; the length of narrow wound channel shortens, diameters of temporary cavities increase when penetration is completed, the gelatin energy and energy transmission ratio increase; The warhead’s tip and location of mass center have a influence on the instable moment of the bullet and length of the narrow wound channel. The instable moment delays and narrow wound channel increases when the warhead's tip flattens. The instable moment moves forward a little and the narrow wound channel shortens a little when location of mass center moves back.

bullet; gelatin; penetration; temporary cavity

In recent years, with the rapid development of the finite element technology, the method of numerical simulation, which could reproduce scenes of the penetration and provide comprehensive information, has been used to reveal the mechanism of terminal effects, predict the power of bullets and judge the effectiveness of bullets. Comparing with experiments, domestic and foreign scholars have achieved remarkable results about the penetration of projectiles into gelatininnumerical simulation. Liu et al.[1]established a two-dimensional motion model for the projectile penetrating gelatin, reflecting the difference between attack angle and yaw angle, and the model has been proven accurately by comparing with the corresponding experimental results. Cronin and Falzon[2]studied effects of temperature, aging time and strain-rate on 10% gelatin, and found that upon increasing strain-rate to 1/s the failure stress increased by a modest amount. Koene and Papy[3]used AUTODYN to study the deformations caused by the penetration of ABS (Acrylonitrile-Butadiene-Styrene) plastic spheres into gelatin at velocities up to 160 m/s. Luo et al.[4]studied the effects of spherical projectiles penetrating the gelatin with different impact velocities, and found that the higher velocity and smaller quality the spherical projectiles had, the faster velocities decreased and the more energy transfered. Wen et al.[5]studied the penetration resistance, stress distribution of the gelatin and the effect of attack angle on the gelatin damage, and observed that angle of incidence had a great effect on the overturning moment of bullets. In addition, Wen[6]discussed the advantages and drawbacks of three formulation approaches employed to simulate the dynamic process of penetration, i. e. Lagrange, ALE and SPH-Lagrange methods, and Ref.[7] experimentally and computationally studied the penetration of a steel sphere into a block of ballistic gelatin for developing an improved understanding of the damage caused to human soft tissues when impacted by a blunt object moving at a moderately high speed.

There are few papers studying the effect of the bullet parameters on the penetration into the gelatin, systematically and quantitatively, with the method of FEM. Here we established a finite element model of the gelatin and a rifle bullet with a diameter of 7.62 mm (hereafter referred to as bullet), and used the finite element software, LS-DYNA, to simulate the penetration. The accuracy of the material model was verified. The effect of the parameters of the bullet on the bullet-gelatin interaction was studied, which includes attack angle, impact velocity, warhead’s tip and location of mass center of warhead. The instable moment of the bullet, length of narrow wound channel, gelatin resistance, gelatin energy and maximum cavity diameter are analyzed. The instable moment is the time when the bullet overturns 10° since entering the gelatin, the length of narrow wound channel in the gelatin is equal to the penetration depth of the bullet in the instable moment and maximum cavity diameter refers to diameter of the temporary cavity at the moment when penetration is completed.

1 FEM model and verification

1.1 FEM modeling of the gelatin and bullet

The bullet consisting of three parts (jacket, lead set and steel core) and a 300 mm×300 mm×300 mm gelatin (10% at 4 ℃) block are used in the experiment and simulation. By observing the pictures captured by a high-speed camera, it is noticed that during the penetrating process, first the bullet becomes unstable , then overtures and finally exits in the off-center place of the gelatin, producing a narrow channel in the beginning and then a elliptical cavity where the maximum diameter of temporary cavity forms in the gelatin.

The 3-D geometries of the bullet and the gelatin were discretized into 27 408 and 1 737 440 8-node brick elements, respectively, shown in Fig. 1. In order to obtain good accuracy of numerical simulation, the gelatin has small elements in the region encompassing the impact area where forming the temporary cavity, and to reduce the amount of mesh, the element size increases as one moves away from this region. The ERODING_SURFACE_TO_SURFACE contact definition is used to simulate the interaction between the bullet and the gelatin and the CONTACT_AUTOMATIC_SINGLE_SURFACE contact definition to simulate the interaction among parts of the bullet. The viscous hourglass control algorithm with hourglass coefficient=0.01 is employed to control the influence of hourglass deformation caused by the large deformation of elements on the reliability of numerical results.

1.2 Material model of the bullet and gelatin

Based on the results of the current research and experiments[8-11], we adopt MAT_JOHNSON_COOK model for the bullet, which is used for problems where the strain varies over a wide range and adiabatic temperature increases due to plastic heating which causes material softening, and use an equation-of-state (EOS_GRUNEISEN) to describe its mechanical response. What’s more, the gelatin is modeled as an elastic_plastic material (MAT_ELASTIC_PLASTIC_HYDRO) with a polynomial equation of state (EOS_ ELASTIC_PLASTIC_HYDRO) to describe its hydrodynamic response. The stress-strain behavior of the gelatin is defined by the material model in the low pressure and pressure-volume behavior by the equation of state under the high pressure. Parameters of the bullet’s material model and the gelatin’s EOS are the same as those in the paper[6].

Fig.1 Finite element mesh of bullet and gelatin

1.3 Model verification

In the verifying experiment, the gelatin was impacted by the 7.62 mm bullet at 625 m/s and attack angle of 1° using a rifle from the front face of the gelatin and a high-speed camera was used to record images to visualize the process of penetration. The size of the temporary cavities is compared with the corresponding experimental size in Fig.2. The length of the cylindrical-like channel at 640 μs in the numerical results differs from the experimental value by 9.37% and the difference between the computed and the test values of the diameter of temporary cavity at 3 520 μs is 2.34%. Furthermore, the comparison of computed and experimental time histories of the penetration depths is exhibited in Fig.3, revealing that the maximum difference is 17 mm at the same moment. It is obvious that the shape of the temporary cavities is very close to the experimentally observed one and time histories of the penetration depth computed are found to agree well with the corresponding experimental results.

Fig.2 Numerical and experimental temporary cavity, shown after the moment of impact at 640 μs and 3 520 μs penetration depths

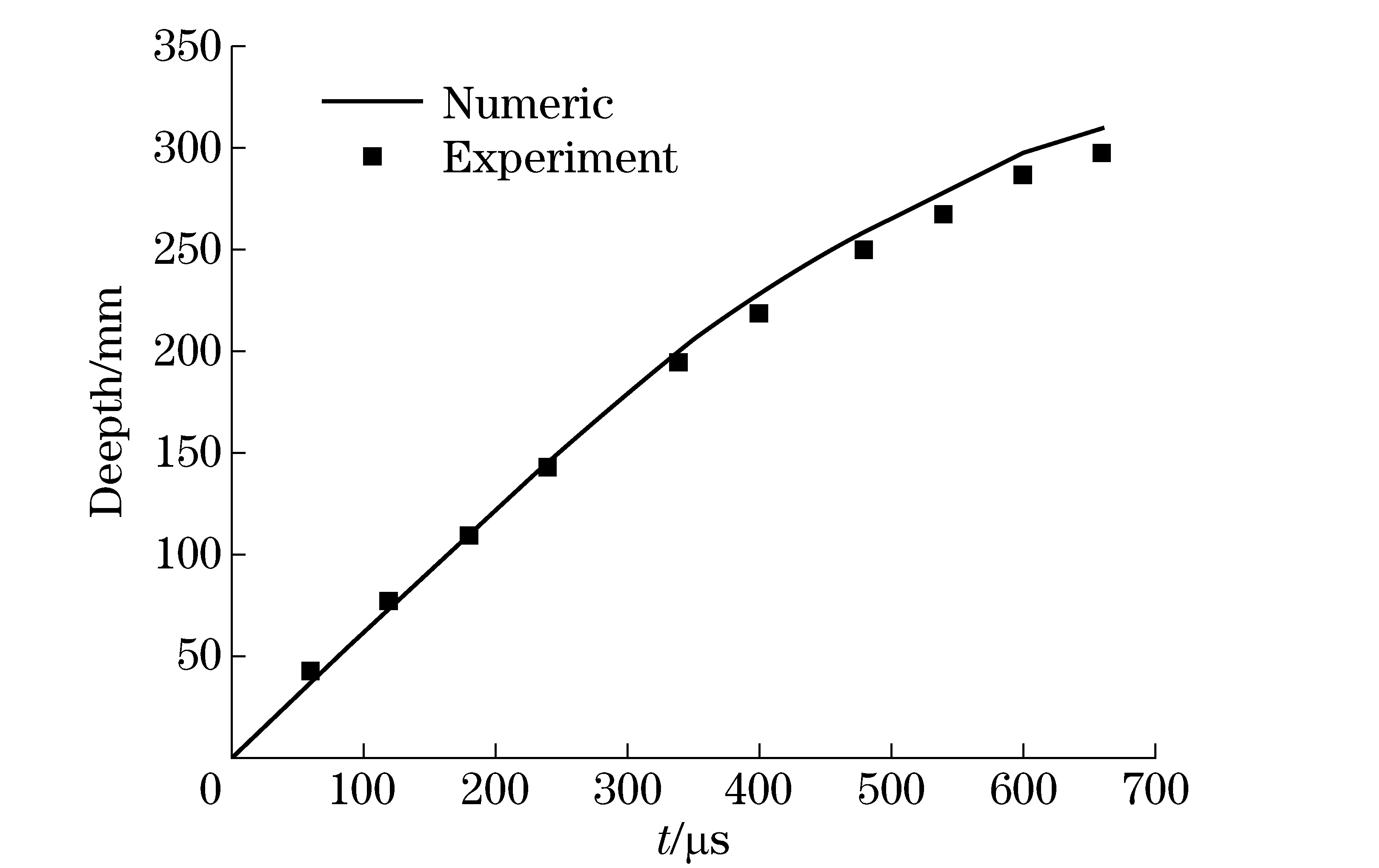
Fig.3 Comparison of computed and experimental time histories of the penetration depths

2 Effect of impact parameters of the rifle bullet

2.1 Effects of attack angle

Different angles of attack (1°, 2°, 3°, 4°) and same impact speed(625 m/s) are employed to study numerically the effects of attack angles on the interaction. In combination with the results plotted in Fig.4 and Tab.1, it can be concluded that the results for the attack angle of 4° compared with that of 1° change a lot, the instable moment is ahead of 43.11%, the length of narrow wound channel decreases 42.45%. Maximum resistance in gelatin changes a little, while the arising moment is ahead of 29.7%. The maximum cavity diameter at the moment of penetration completed increases by 17.57% and the decrement of the exiting speed of the bullet increases by 13.45%. Maximum gelatin energy increases by 6.95% and the energy transmission ration increases by 5.32%.

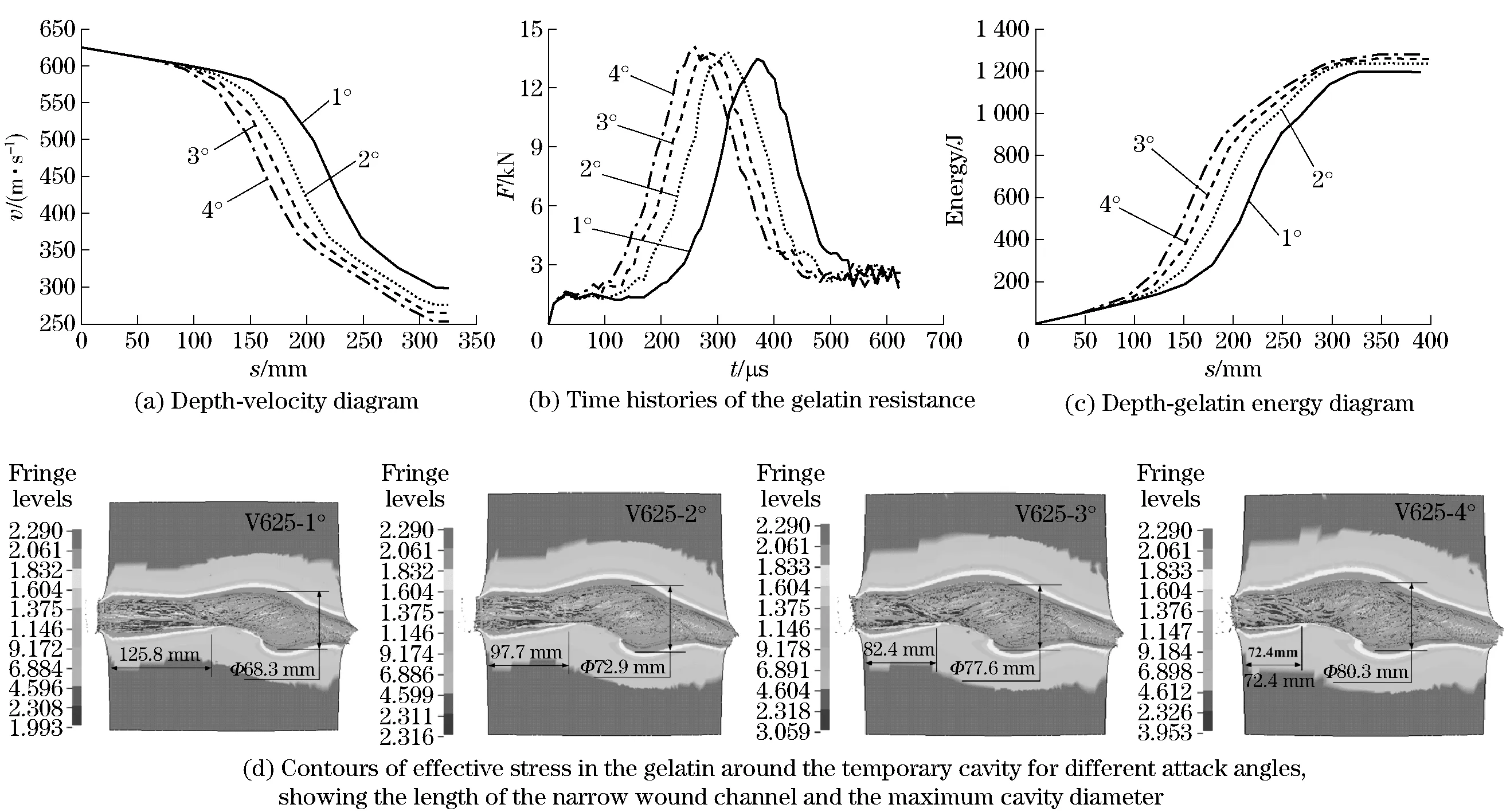
Fig.4 Computed results of different attack angles (1°, 2°, 3°, 4°)

2.2 Effects of the impact velocity

To study the effect of the impact speed on the interaction, three simulations labeled A, B and C in Tab.1 are employed. The bullets have the same attack angle of 3° and different impact velocities (500 m/s, 625 m/s, 700 m/s). Combining the results plotted in Fig.5 with the values listed in Tab.2, it is observed that taking results for simulation A as the reference, 25% and 40% change in the impact velocity alters, respectively, the instable moment by -20.27% and -28.57%, the maximum resistance on the gelatin by 38% and 72.31%, the gelatin energy by 53.61% and 101.4%. The length of narrow channels, maximum cavity diameters, attenuation ratio of the velocity and energy transmission ratio change little at the moment of penetration completed.

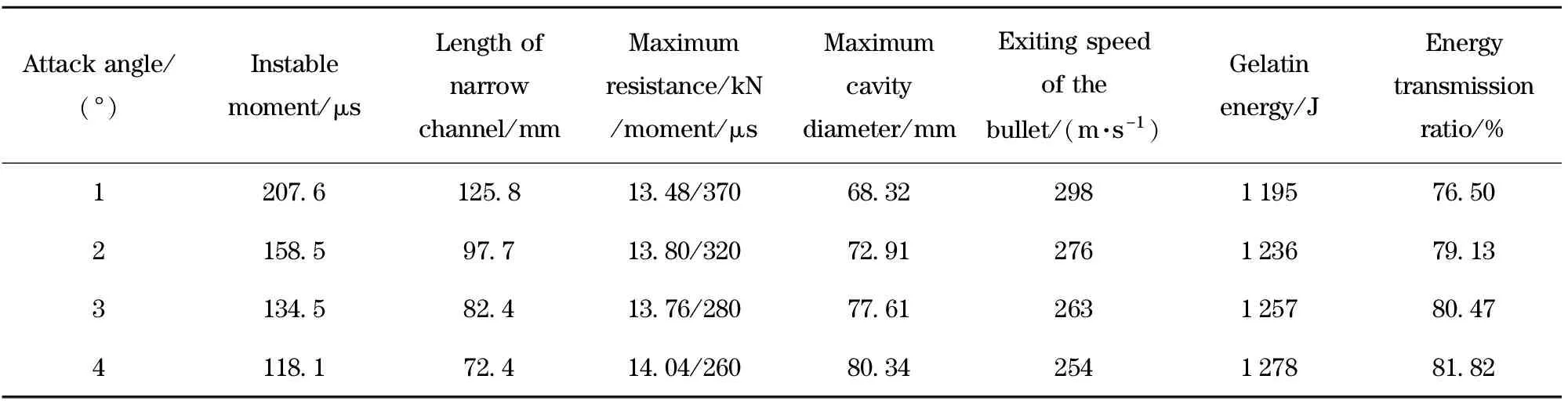
Tab.1 For the impact velocity of 625 m/s, computed results for four values of the attack angle

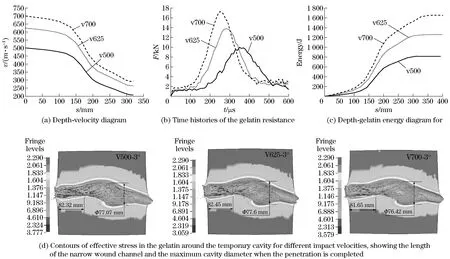
Fig.5 Computed results for the different impact velocities (625 m/s, 500 m/s, 700 m/s)

Tab.2 For the attack angle of 3°, computed results for three values of the impact velocity

No．Impactvelocity/(m·s-1)Instablemoment/μsLengthofnarrowwoundchannel/mmMaximumresistance/kNMaximumcavitydiameter/mmExitingspeedofbullet/(m·s-1)Attenuationratioofthevelocity/%Gelatinenergy/JEnergytransmissionratio/%A500168 782 39 9777 0720658 80818 380 65B625134 582 413 7677 6126357 92125780 47C700120 581 617 1876 4229158 43164882 72

2.3 Effect of the warhead tip

For the impact speed of 625 m/s and attack angle of 3°, the effect of the warhead tip is investigated by modifying the head’s shape of the bullet. Based on the geometry of the ordinary rifle bullet used in the previous chapters, warhead is modified into a flat head (the modified bullet is called flat bullet in this paper), trying to ensure the same quality and the maximum pressed area in the gelatin. The results shown in Fig.6 reveal that compared with the ordinary bullet, the instable moment of the flat bullet is 154 μs , delayed 10.03% and the length of narrow wound is 94.32 mm, an increase of 14.37%, the maximum resistance is 13.85 kN, therefore little is changed. The maximum cavity diameter, the exiting speed of the bullet, the gelatin energy and energy transmission ratio are especially 75.82 mm, 266 m/s, 1 247 J and 79.83% at the moment of penetration completed, substantially the same with that of the computed results of the ordinary bullet.

2.4 Effect of the centroid of the bullet

For the impact speed of 625 m/s and attack angle of 3°, the effect of the location of the bullet mass center is studied by simulating the penetration of a special bullet into the gelatin, in which the steel core is divided into two parts. To get the modification of the centroid of the bullet, the ratio of the density of the two parts in the steel core is matched, assuring the quality of the bullet unchanged. In the simulation, two models of the special bullet are created with centroid forward and backward (forward_bullet and backward_bullet).

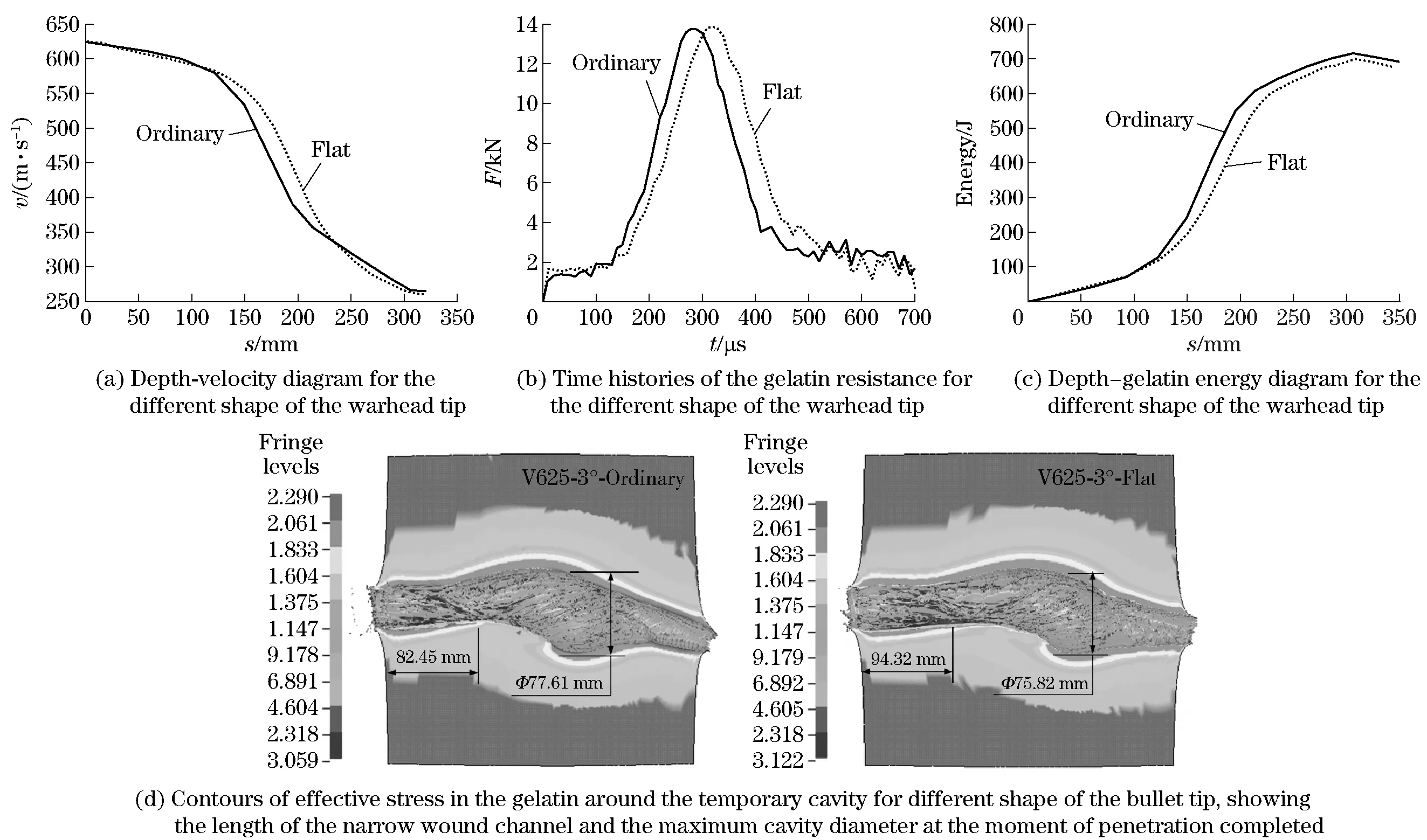
Fig.6 Computed results for the different shape of the bullet tip

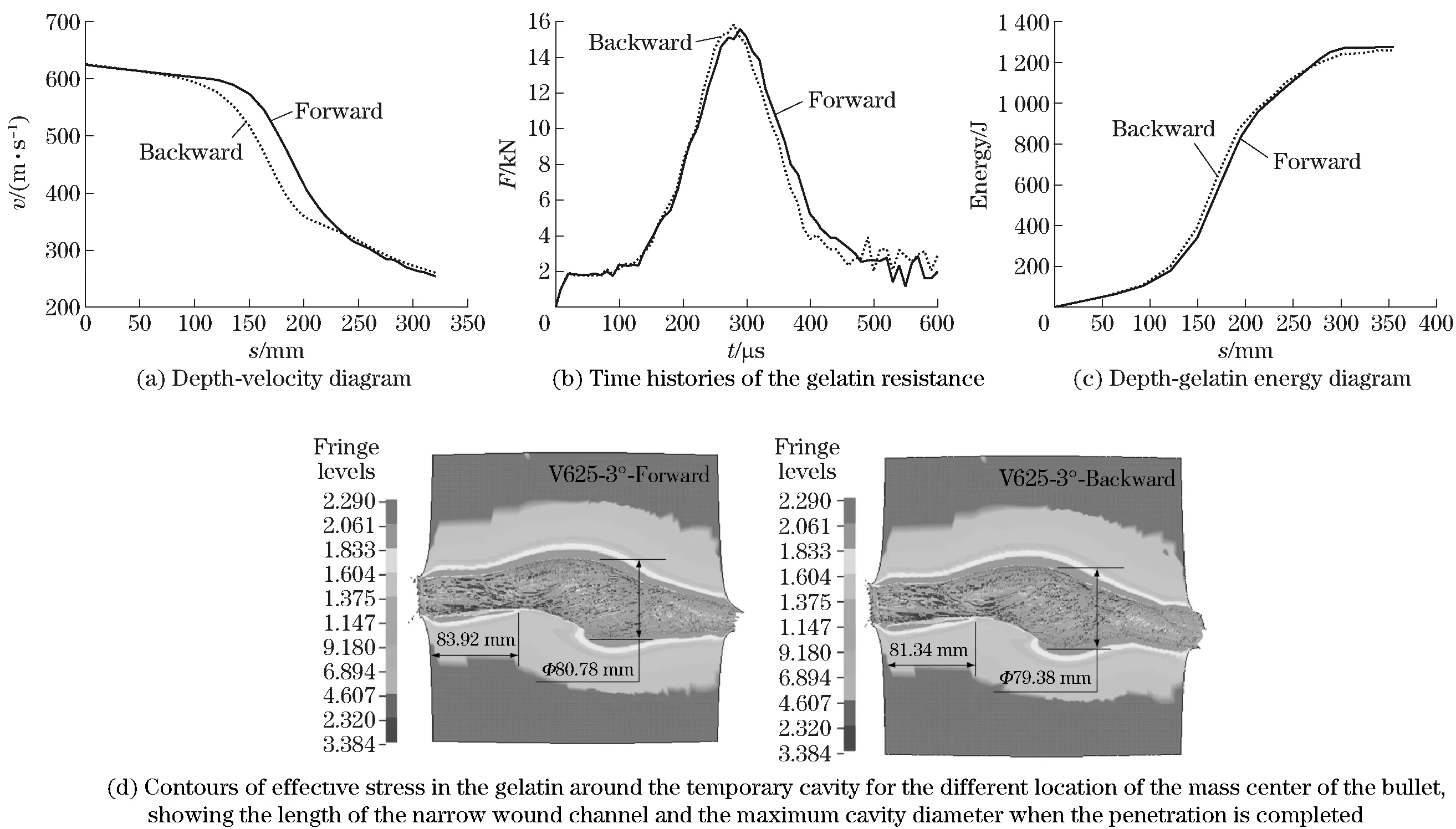
Fig.7 Computed results for the different location of the mass center of the bullet

Comparing the result of the forward_bullet with that of backward_bullet shown in Fig.7, the instable moment is ahead of 2.28%, the length of narrow wound channel shortens 3.07%, the maximum resistance in gelatin is basically the same. The maximum cavity diameters, the exiting speed of the bullet, the gelatin energy and energy transmission ratio change little at the moment of penetration completed.

3 Conclusion

We have established a finite element model of the bullet_gelatin penetration and verified the validity and accuracy of the model by comparing thecomputational results with those observed experimentally. Based on the analysis of the simulation with different sets of parameters, the influences on the results with the change of parameters are understood quantitatively and following conclusions are drawn. With the increase of the attack angle, the instable moment is moving ahead, the length of narrow wound channel shortens, the maximum cavity diameter and energy transmission ratio increase. The higher the impact velocity is, the greater the gelatin resistance and the more the gelatin energy will be. Compared with the computational results of the ordinary bullet, the instable moment delays and the length of narrow wound channel shortens when the shape of the warhead tip is modified to be flat. The location of the mass center of the bullet has a little influence on the instable moment and narrow wound channel in the gelatin. A bullet with the centroid backward compared with the ordinary bullet overturns earlier and the length of narrow wound channel is shorter.

[1] Liu Kun,Wu Zhilin, Xu Wanhe, et al. A motion model for bullet penetration gelatin [J]. Explosion and Shock Waves, 2012,32(6): 616-622.(in Chinese)

[2] Cronin D S, Falzon C. Characterization of 10% ballistic gelatin to evaluate temperature, aging and strain rate effects[J]. Exp Mech, 2010,51:1197-206.

[3] Koene L, Papy A. Experimental and numerical study of the impact of spherical projectiles on ballistic gelatin at velocities up to 160 m/s [C]∥25th International Symposium on Ballistic, Beijing, 2010:1573-1579.

[4] Luo Shaomin,Huang Gongwu,Chen Aijun,et al. Numerical simulation analysis of spherical projectiles penetrating gelatin [J]. Computer Simulation, 2012,11: 79-82. (in Chinese)

[5] Wen Yaoke, Xu Cheng, Chen Aijun,et al. Numerical simulation of the penetration of bullet on gelatin target[J]. Acta Armamentarii,2013,1:14-19. (in Chinese)

[6] Wen Yaoke, Xu Cheng, Chen Aijun,et al. Numerical simulation of spherical fragments penetrating into ballistic gelatin at high velocity[J]. Journal of Ballistics,2012,24(3):25-30. (in Chinese)

[7] Wen Yaoke, Xu Cheng, Wang Haosheng, et al. Impact of steel spheres on ballistic gelatin at moderate velocities [J]. International Journal of Impact Engineering, 2013,62:142-151.

[8] Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strains,high strain rates and high temperature[C]∥Proceedings of the 7th International Symposium on Ballistics, Hague, Netherlands, 1983:541-547.

[9] Jenq S, Hsiao F, Lin I, et al. Simulation of a rigid plate hit by a cylindrical hemi-spherical tip-ended soft impactor [J]. Computational Mater Science ,2007,39(3):518-526.

[10] Ensen M N, Zimcik D G, Lahoubi M, et al. 07-CSME-66-Soft body impact simulation on composite structures [J]. Transactions of the Canadian Society for Mechanical Engineering, 2008,32(2): 283-296.

[11] Nestor N. Theoretical study of the motion of a rigid gyro-stabilized projectile into homogeneous dense media[C]∥Preceedings of the 24th International Symposium of Ballistics, New Orleans, 2008.

(Edited by Wang Yuxia)

10.15918/j.jbit1004-0579.201524.0409

TP 391.9 Document code: A Article ID: 1004- 0579(2015)04- 0487- 07

Received 2014- 02- 15

E-mail: 927838726@qq.com