基于一般变权方法的直流落点选择
刘平坚,蔡金锭,李天友,林因,江伟
(1.福州大学电气工程与自动化学院,福建 闽侯 350108;2.福建省电力有限公司技术中心,
基于一般变权方法的直流落点选择
刘平坚1,2,蔡金锭1,李天友3,林因4,江伟4
(1.福州大学电气工程与自动化学院,福建 闽侯 350108;2.福建省电力有限公司技术中心,
福建 福州 350007;3.福建省电力有限公司,福建 福州 350003;4.福建省电力有限公司电力科学研究院,福建 福州 3530007)
直流落点选择是一个典型的多目标决策问题。选取静态电压稳定、有效短路比、系统有功功率损耗作为该多目标决策问题的三个指标。并运用一般变权原理来求解这一问题。相对于线性加权法和平方和加权法具有较好的均衡性,更符合人的决策思维。
多目标决策;变权;直流落点选择;激励策略
1 引言
直流输电作为成熟、可靠的技术,未来将继续在中国西电东送工程中发挥重要作用,预计至2020年中国将有数十回直流输电工程建成投运,期间,必然将给受端系统带来诸多新问题。其中,直流落点选择是电网规划中需要解决的重要问题之一,合理的落点方案将极大地改善电网安全稳定运行水平。
直流落点选择是一个非常复杂的系统决策问题,其中需要考虑决策目的、系统安全、经济性、工程实施等多方面[1-3]。在目前大电网规划中,通常基于电网送受电关系,由规划设计人员直接制定有限数量的直流落点方案,在此基础上进行安全稳定性、经济性等方面的计算分析与评估,通过结果比较确定最终直流落点规划方案[4-6]。这种评估方法能够同时考虑多种因素影响,但由于每个直流落点方案安全稳定性和经济性等评估工作量大,很难对所有方案进行评估比较,初始方案的制定在很大程度上需要依靠规划设计人员的工作经验,缺少对所有可能方案进行大面积初步筛选的工作环节和技术手段。文献[7]从有效短路比、静态电压稳定指标和有功功率损耗三方面提出了基于线性加权和法建立目标函数的直流落点选择方法,克服了依靠规划设计人员确定直流落点规划方案时需要进行大量的评估工作的缺点,但该选择方法仅仅考虑到各类指标在决策中的相对重要性,而忽略了对状态均衡程度的偏好,这种“以不变应万变” 的做法具有一定的片面性;同时,有效短路比与静态电压稳定指标之间存在着一种相互转换的关系,基于线性加权和法的多目标决策方法的加法性质有可能使决策失去应有的准确性。
为解决直流落点选择研究进程上所存在的缺陷,本文同时考虑人们对单因素子目标的诸状态的效用与各指标间的不可替代性,提出一种基于求多目标决策的激励策略可行解的直流落点选择方法和流程。
2 直流落点选择的三大主要影响因素
目前在选取直流落点时,主要考虑三点影响因素,静态电压稳定指标(VSI)、有效短路比(ESCR)、系统的有功功率损耗Psun。并且前两者的数值越大,第三者的数值越小说明所选取的直流落点越理想。
2.1 静态电压指标(VSI)
静态电压稳定性分析在实际上相当于发动机经过某一阻抗给一个负荷供电的过程中对此负荷母线电压稳定的分析,判定指标为:
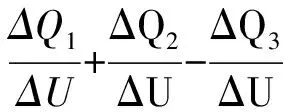
式中,Q1为交流无功功率;Q2为直流无功功率;Q3为交流滤波器和补偿电容的无功功率。
当VSI>0时静态电压稳定;当VSI<0时静态电压不稳定。
2.2 有效短路比(ESCR)
评价受端电网的电压支撑能力于接受直流功率的能力主要由交流系统相对比直流系统容量比值的大小决定。电网的规划中主要是引入有效短路比来衡量交流系统的强弱。其定义为:
式中,S为交流系统短路容量;Q为无功补偿容量;P为直流换流器额定容量。
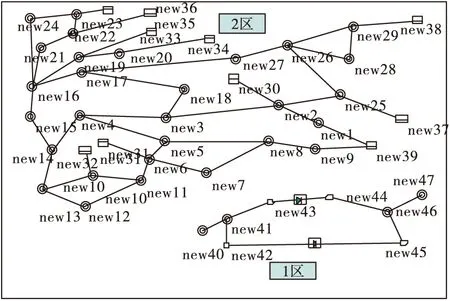
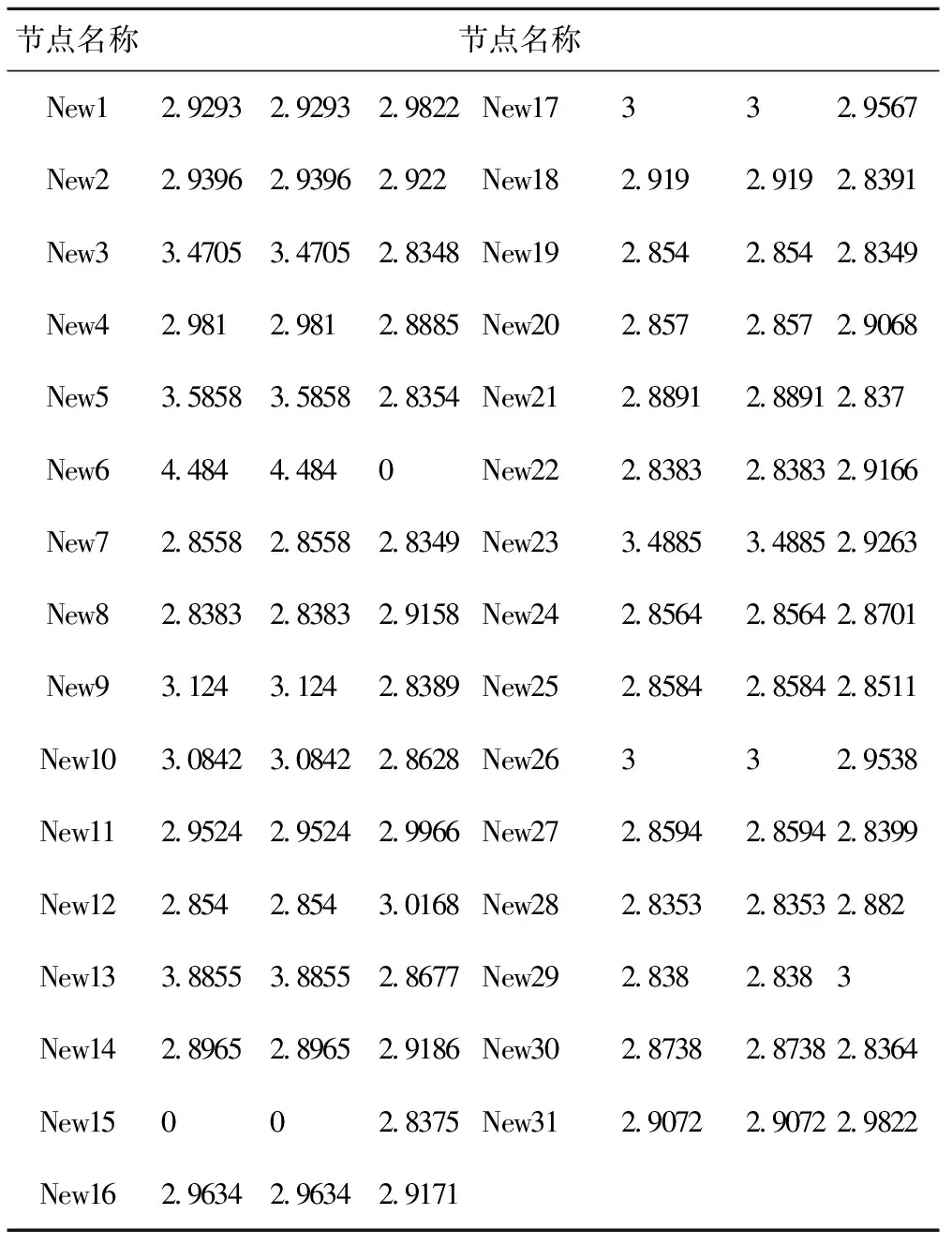
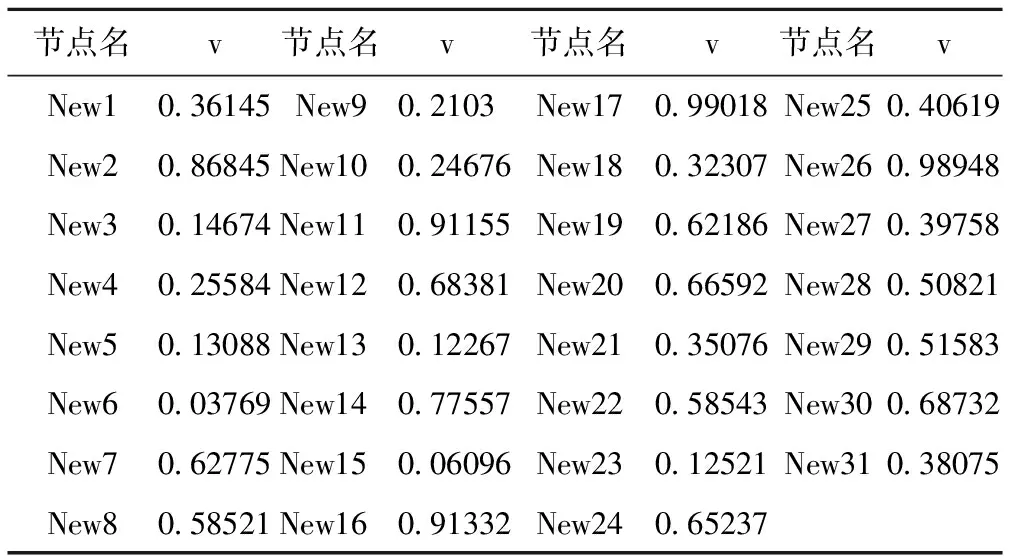
一般我们认为ESCR>5时为强交流系统;3 2.3 系统有功功率损耗 由于受端交流系统潮流分布会随着直流落点所选择的改变而改变,伴随着系统的网损也会发生相应的改变。因此在选择直流落点的同时应尽量将网损做到最小保证系统运行的经济性。交流系统有功功率损耗定义为Psun: 式中:Nm为系统之路数;Gm(i,j)为支路电导;Vi,Vj,θi,θj为各节点电压的幅值和相角。 3.1 指标的隶属度函数及其满意度 直流落点选择以尽量降低受端系统整网的有功损耗、达到降耗的经济性目的,同时,基于受端系统安全稳定性的需要,尽量提高有短路比(ESCR)及静态电压稳定值(VSI)。 基于此,直流落点选择的多目标模型为: maxF(x)={f1(x),f2(x),-f3(x)};s.t.gi(xj)≤0,i=1,2,3,j=1,2,…,n. (1) 其中:x为n维优化向量;gi(x)为多目标决策模型约束函数;f1(x),f2(x),f3(x)分别为短路比、静态电压稳定值与有功损耗三个指标的目标函数。 由于上述目标函数没有统一的度量标准,难以进行比较,鉴于此,引入每个目标函数的隶属度函数的定义如下: (2) 满足:(1)0≤μi(fi)≤1;2)μi(fi)关于fi单调递增;上式fi*和fi′分别为第i个单目标决策模型的最优解和最劣解,称f*=(f1*,f2*,…,fm*)和f′=(f1′,f2′,…,fm′)分别为多目标决策模型解域中的理想点和负理想点。 同时,根据(2)式可得目标函数的满意度定义为: (3) 式中fip为在目标函数fi上决策者希望达到的水平值,即目标函数fi的期望值。 经过上述介绍,易知引入隶属度函数μ来进行直流落点选择的多目标规划模型的建立,完成了对各指标的归一化处理,即统一了指标间的度量标准;因此,接下来需将多目标的最优模型转化为单目标模型。 3.2 基于协调度原理的最优变权 多目标决策问题的求解难度较大,需将多目标模型转化为单目标模型以简化计算,普遍的做法是通过常权达到这一目的,但这种以不变应万变的做法可能会使决策结果与事实背道而驰。所以,本文提出一种最优变权的方法,不仅克服了传统做法的片面性缺点,而且基于协调度原理,求得具有最优效果的变权,使得多目标转换成单目标这一过程更具合理性。 3.2.1 一般变权原理及步骤 变权的类型有三类,与其激励策略p的取值有关,即变权的激励效用族决定,分别有惩罚型(pj=e)、激励型(pj=0)与折衷型(pj∈(0,1))。 若激励效用族﹛uj(t)﹜(j=1,2,…,m)满足0≤uj(t)≤1(t∈(0,1),j=1,2,…,m),则称﹛uj(t)﹜(j=1,2,…,m)是正规的。变权的效果好坏与激励效用族﹛uj(t)﹜(j=1,2,…,m)有着直接的联系,而变权的效果评价指标为协调度且定义如下: 设w(x)为变权,w(0)为常权,故因素的状态组合x关于w(x)与w(0)的协调度为: (4) 若ρ(x)>1,则称x关于w(x)与w(0)是协调的;ρ(x)<1,则称x关于w(x)与w(0)是不协调的;若ρ(x)=1,则称x是临界的。 一般情况下,变权的步骤为先由专家给出反映诸因素(子目标)相对重要程度的常权w(0)和反映诸因素状态的及格水平的激励策略p(即(3)式中的目标函数满意度),然后遵循协调原理来构造变权(多为某效用函数族诱导的变权)。 具体步骤如下:(1)已知专家赋予的常权w(0)和激励策略p;(2)根据协调原理,构造出激励效用族﹛uj(t)﹜(j=1,2,…,m)如: (5) 式中:μ为各目标函数隶属度函数,p为目标函数满意度,m为目标函数个数(本文中m=3),α与c定义如下: (6) 然后,即可求由激励效用族诱导得到的变权 (7) 最终可以得到多目标规划模型的求解模型为 maxv=wT(μ)μ; s.t.gi(xj)≤0,i=1,2,3,j=1,2,…,n. (8) 式中,μ=[μ1μ2μ3]T为各指标的隶属度函数值矩阵。 4.1 系统模型 本文目标函数所采用的算例如图1所示由两个区域组成。区域1为39节点的受端交流系统,区域2为直流系统。将节点40作为直流的送端向区域2搭建一条直流线路。从区域2中选择一个稳定性与经济性最优的节点作为直流落点。 图1 系统接线图 4.2 分析 本文采用BPA电力系统仿真软件对2区中的各个节点的ESCR、VSI、Psun进行计算并做归一化处理得出相应的隶属度函数值如表1所示。本文采用折衷型激励策略。已知专家赋予的常权w(0)=[0.4444、0.4444、0.1112]。由公式(6)计算得到α=0.6667,c=2.834。由公式(5)得到激励效用族的微分见表2。由公式(7)可得到有激励效用族诱导得到的变权w(x)见表3。最后由公式(8)得到目标函数值。从表4中可以看到17节点是最优的直流落点。 表1 隶属度函数值 表2 激励效用族的微分 表3 变权w(x) 表4 目标函数值(v) [1] 徐政.交直流电力系统动态行为分析[M].北京:机械工业出版社,2004. [2] 刘崇茹,张伯明.交直流混合输电系统灵敏度分析[J].电力系统自动化,2007,31(12):45-49. [3] 穆子龙,李兴源.交、直流输电系统相互影响引起的谐波不稳定问题[J].电力系统自动化,2009,33(2):96-100. [4] 郭小江,郭剑波,马世英,等.基于多馈入短路比的多直流落点选择方法[J].中国电机工程学报,2013,33(10):36-42. [5] 周勤勇,刘玉田,汤涌.计及直流权重的多直流馈入落点选择方法[J].电网技术,2013,37(12):3336-3341. [6] 陈虎,张英敏,贺洋,等.多馈入直流输电系统功率稳定性分析[J].电网技术,2011,35(6):50-54. [7] 王康,刘崇茹,韩民晓,等.兼顾稳定性与经济性的交直流系统直流落点选择方法[J].电力系统自动化,2011,35(24):73-78. [8] 刘文奇,余高锋,胥楚贵.多目标决策的激励策略可行解[J].控制与决策,2013,28(6):957-960. [9] 蔡前凤,李洪兴.均衡度与变权[J].系统工程理论与实践,2001,21(10):83-87. [10] 汪培庄.模糊集与随机集落影[M].北京:北京师范大学出版社,l985. DC Point Election Based on Variable Weight Method LIUPing-jian1,2,CAIJin-ding1,LITian-you3,LINYin4,JIANGWei4 (1.Electrical Engineering and Automation College of Fuzhou University,Minhou 350108,China;2.Fujian Electric Power Co.,Ltd.,Fuzhou 350007,China;3.Fujian Electric Power Co.,Ltd.,Fuzhou 350003,China;4.Fujian Power Science Research Institate of Power Co.,Ltd.,Fuzhou 350007,China) The DC point selection is a typical multi-objective decision problem.This article selects the static voltage stability,effective short-circuit ratio,the system active power loss as the three indicators of multi-objective decision problem.And using general variable weight principle to solve the problem.Compared with the linear weighted method and the weighted sum of squares method has a good balance,more in line with the thinking of people. multi-objective decision-making;variable weight;DC point selection;incentive strategy 1004-289X(2015)04-0026-04 TM71 B 2014-06-24
3 直流落点选择多目标决策模型
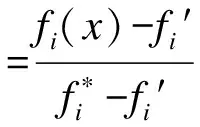
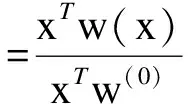


4 算例分析