铁路车站人员应急疏散仿真研究
罗培卿,李续扬
(兰州交通大学 交通运输学院,甘肃 兰州730070)
随着我国政府对铁路投资力度的不断加大,许多大型铁路客运站也相继建成并投入使用,但由于站内内部设备多、布局结构紧凑、建筑材料不同,并且人员流动性大、人群密集性高、行为多样性等特点,一旦站内发生突发性事件,站内人员在疏散不理想的情况下极易产生恐慌,给站内或站外的密集人群带来严重影响。
在现实情况中很难对突发性事件进行实验,并且很难通过分析人群在疏散过程中的运动学规律来建立数学模型,以便来模拟突发性事件。因此,通过计算机仿真学来对人员疏散进行建模,是当前研究应急疏散问题的主要方法。计算机仿真学研究的人员应急疏散方法主要有宏观方法、微观方法和中观方法三类。
1 基于Agent的建模仿真方法
上世纪90年代,基于个体Agent的建模理论和技术不断向前发展,且引起了相关领域研究学者的高度重视,如集聚经济、市场需求、人口的快速增长、空间的相互作用等整合到一个框架之中。通过结合Agent建模理论及仿真学理论,对复杂系统中的各个体行为进行建模,并对个体的行为和交互关系进行描述,刻画出一个复杂系统的行为。
建模要素如下:
1.1 Agent
与一般的数学建模不同,Agent建模属于行为建模。基于Agent的建模框架包括以下三个部分:
1)感知部分,个体Agent接受信息;
2)认知处理部分,主要包括学习、规划事务处理等;
3)行为输出部分,输出行为并且影响外界环境。
1.2 环境空间
Agent作为一个可计算实体,它的决策动作是通过感知复杂环境的动态变化,来达到预定的目标。因此,在人员疏散仿真中,物理空间作为Agent赖以生存的基础,如何表示物理在整个模型中的作用显得非常重要。
2 仿真模型的建立
2.1 环境模型
由于铁路车站的特殊性,如何快速地将铁路车站的要疏散人员从危险区域向安全区域疏散,是人员疏散的本质问题,因此,如何表示个体所处的空间位置已成为仿真技术中的关键问题。
为保持连续铁路车站的空间仿真优势,采用与笛卡儿坐标系一致的连续空间物理坐标(x,y)来表示智能体Agent的自身运动学变量。
由于二维网格离散空间模型能够降低计算机的仿真难度,因此本文将采用二维网格(平面空间划分成0.5m×0.5m的正方形网格)离散化空间模型来表示智能体Agent的对外表现和仿真中的可视化,每一个网格某一时刻的状态只有三种:障碍、被占据及空闲。其中网格坐标为(xi,yj),分别代表智能体Agent所在网格的行和列。当智能体Agent运动时遇到障碍或被占据时网格状态为1,当为空闲时为0。
根据上述约定可知,当某一网格状态被智能体Agent感知为1时,表示该网格所代表的区域不可用,当状态为0时,则表示可用。为表示方便,约定当智能体Agent(x,y)落在某一网格时(此时的坐标指的是物理坐标),则认为该网格的全部区域被智能体Agent占据了。因此,当智能体Agent到达目的地(出口)时,也就是说该智能体Agent的物理坐标落在了目标网格中。
2.2 智能体属性
对一群智能体Ak(k=1,2,…,n)按照如下定义其属性

2.3 智能体的运动决策体系
“感知-决策-行动”这一循环是智能体Agent的活动行为。智能体Agent结合自身的内部状态和对环境的观察来决定目标选择和路径规划。对局部相邻环境的感知也是智能体Agent仿真技术的重要组成部分。
目标选定后,智能体Agent的移动速度完全由人员疏散运动学模型和障碍物来决定。此时的智能体Agent的运动行为并不能完全由Agent的感知和判断来避免与动态障碍物的冲突,当出现碰撞冲突时,智能体Agent需要对当前的动作进行临时调整。
3 人员疏散的可计算模型
3.1 感知
智能体Agent从当前位置向目标位置移动的过程中,其位置是由智能体Agent的速度大小和方向变化决定的。环境的变化及智能体自身内部状态的变化是智能体Agent的速度改变依据。
3.2 决策
3.2.1 人员疏散的路径规划
人员疏散过程,就是疏散人员为了躲避障碍物而选择策略,并向目标方向选择路径移动的过程。如何使得疏散人员到达出口需要通过的路径最短是路径选择的一般依据。
基于上述约定,采用基于子目标最短路径规划的算法来对路径进行选择。具体方法如下:当出口在疏散人员的视觉范围之内或者移动途中没有障碍物阻挡(不包括人阻挡),称之为直接可达,此时疏散人员沿着出口方向直线移动;否则,疏散人员将从子目标库中选择一个直接可达的子目标,然后向子目标方向移动,当到达子目标后再向出口方向移动,如果期间过程中还是不直接可达的话,再从中选一个中间子目标,依此类推。约定人群在向子目标疏散过程中所走的路线为直线,总的行走路线是折线或者直线形式。
子目标的选定方法:个体Agent通过路线折线每一段的两个端点附近,如图1所示。
图1中A代表障碍物,B代表疏散个体,C代表出口,x代表子目标,图1中箭头标示的折线为个体B疏散时的行走路径。
3.2.2 速度大小的确定
影响铁路车站人员速度大小的因素主要有:
1)先前的速度大小,由于任何物体都具有惯性,速度具有连续性的运动特性,所以应尽可能地避免超过因人体突然加速或者减速而产生的起动生理特性;
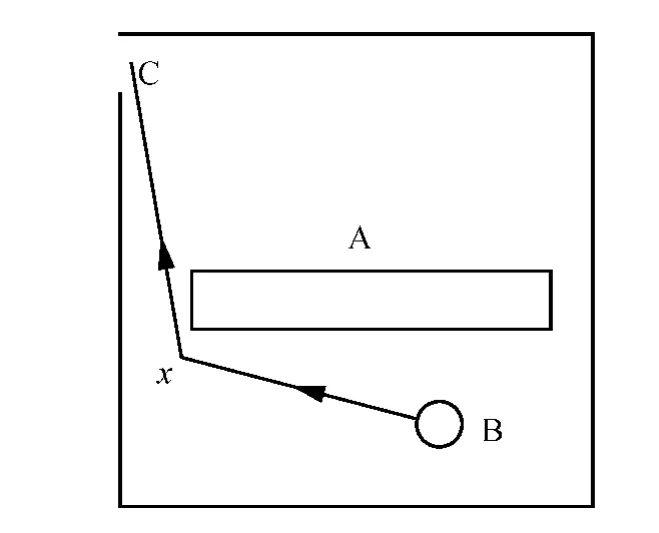
图1 基于子目标的最短路径规划
2)所处位置人群密度的影响;
3)个体心理恐慌及其他因素的影响。
因此综合考虑个体先前速度的延续性和周围人员密度对速度的影响,通过拟合一定的比例关系,两种因素同时包含在内,此时速度表示为

式中:U为密度-速度经验公式;λ为量化先前经验程度,且
在铁路车站的平直通道中,行人的行走速度与群集的密度关系为
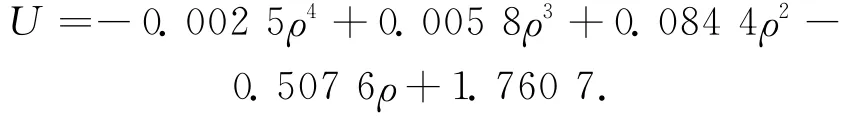
在铁路车站的楼梯中,行人的行走速度与群集密度的关系为

式中:ρ为个体所处位置的人员密度。
对于其他因素的干扰项,定义如下的随机函数

式中:p为因心理恐慌、其他因素对个体造成的影响程度,一般取值为0;random为区间均匀分布随机函数。
综上所述,得到总速度大小公式为
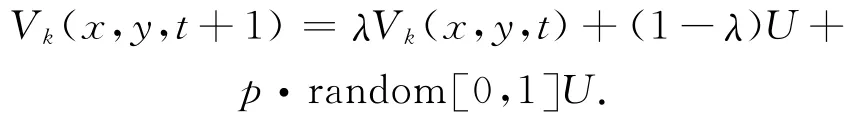
3.2.3 速度方向的确定
个体运动方向的影响因素主要有:
1)人由于习惯而沿着当前运动方向不作改变的概率;
2)目标吸引,个体在任何时候、任何地点都是朝着目标(出口)行进的;
3)环境空间的约束或者运动方向上存在其他疏散人员的阻挡;
4)个体心理恐慌及其他因素的影响。
由于人的习惯性,个体在由当前方向角转向下一步方向角时有一定的延迟以及保留,基于上述影响,个体在下一步移动的方向角可表示为

式中:θk(x,y,t+1)为下一步个体的运动方向角,θk(x,y,t)为当前个体的运动方向角,αk(x,y,t)为物体运动与目标间的偏离角,参数λ同上。
设目标所处的坐标为(Xk,Yk),智能体Agent与目标间的距离为

智能体Agent到目标的方向角为

因此,当前运动方向与目标方向的偏角为

当目标的吸引而导致大小为λαk(x,y,t)转向角转向后,此时因个体运动时遇到障碍而不能顺利向目标方向行进时,个体应对障碍做出反应,此时在θk(x,y,t+1)=θk(x,y,t)+λαk(x,y,t)为方向角的基础上,个体以一定的概率调整下一步运动方向,定义为

目标吸引发挥影响之后,由于车站内的障碍物或其它环境的因素而造成疏散个体的心理恐慌,该项因素是独立于其它随机扰动项而发挥作用,该微量扰动可表示为

综上可得出总的方向转角

因此最后个体的运动方向为

3.3 动作
在个体的运动速度和运动方向均已知的情况下,如若在移动过程中没有遇到障碍物,个体将朝着目标位置方向移动;当个体运动过程中遇到障碍物,应先停在原处不动对运动个体进行临时方向调整,再做出下一步的决策,具体如表1、表2、表3所示。

表1 恐慌级别的影响

表2 速度大小惯性的影响

表3 速度方向惯性的影响
4 疏散仿真模拟
4.1 系统仿真
根据构建的模型,利用现有软件Swarm对西安站售票厅乘客的疏散进行仿真模拟,在仿真开始时设定:人员运动方向惯性、人员恐慌等级、人员运动速度惯性的三个模型参数,且每种组合执行15次系统的仿真模拟。设定在仿真开始时,在售票厅共有200人停留,所得数据如表(其中“-”表示疏散时间增震荡过大,不可预测)1所示。
4.2 仿真结果分析
从表1的仿真数据可以看出,人员疏散时间受疏散人员心理恐慌的影响较大,并随着恐慌程度的增加,人员的疏散时间会明显增加。从表2看出,只要个体速度不是由当前速度完全确定,速度惯性的变化影响就不大。从表3可以看出,只要适当的维持疏散个体的当前运动方向,疏散时间并不会明显的延长;当个体过分偏离目标方向时,疏散时间才会急剧增加。
5 结束语
本文在总结基于Agent技术的理论基础上,提出一种针对人员疏散的Agent技术运动学可计算模型;然后再利用现有的软件进行仿真,仿真结果与现实情况比较吻合,同时也可以在仿真过程中的任何时刻对人群的疏散过程及人群的整个分布状况进行动态观察,从中找出疏散瓶颈,为现实工作提供指导。
[1] Kirchner A,Schadschneider A.Simulation of evacuation processes using a bionics-inspired cellular automaton model for pedestrian dynamics[J].Physica A:Statistical Mechanics and its Applications,2002,312(1):260-276.
[2] Blue V J,Adler J L.Cellular automata microsimulation for modeling bi-directional pedestrian walkways[J].Transportation Research Part B:Methodological,2001,35(3):293-312.
[3] Lovs G G.Models of way finding in emergency evacuations[J].European Journal of Operational Research,1998,105:371-389.
[4] Henderson L F.The Statistics of Crowd Fluids[J].Nature,1971,229(5284):381-383.
[5] 崔喜红,李强,陈晋,等.基于多智能体技术的公共场所人员疏散模型研究[J].系统仿真学报,2008,20(4):1006-1010.
[6] 陆君安,方正,卢兆明,等.建筑物人员疏散逃生速度的数学模型[J].武汉大学学报:工学版,2002,35(2):66-70.
[7] 陈绍宽,李思悦,李雪,等.地铁车站内乘客疏散时间计算方法研究[J].交通运输系统工程与信息,2008,8(4):101-107.
[8] 胡清梅,方卫宁,李广燕,等.地铁车站出口布局对人群疏散性能的影响[J].铁道学报,2009,31(3):111-115.
[9] 习江鹏.西安市城市轨道交通运营安全管理[J].交通科技与经济,2014,16(5):58-61.

