带时间窗的多车型车辆路径问题研究

陈 磊

（兰州交通大学 交通运输学院，甘肃 兰州730070）

车 辆 路 径 问 题 （Vehicle Routing Problem，VRP）已被证明是NP难题，带时间窗的车辆路径问题（Vehicle Routing Problem with Time Windows，VRPTW）由于增加了时间约束，使得问题在求解中变得更加复杂，VRP为组合优化问题，本文选用的配送车辆为多车型，这使得问题的解呈几何型增长，当配送点的数目增大时，采用精确算法很难求得问题的精确解。因此用启发式算法在一定的时间内求得问题的满意解已成为研究的主要方向。

Dorigo等人首先提出了蚁群算法，它是一种新的种群启发式算法，利用一群人工蚂蚁的协同工作来进行寻优，每只蚂蚁都遵循一定的规则随机选择下一个节点，并在到达下一节点后释放一定量的信息素，从而对下一只蚂蚁起到引导作用，最后蚂蚁将会倾向于选择路程最短的路径。其具有很强的鲁棒性，是解决组合优化问题的有效手段，该思想已被应用到各个研究领域，并取得了大量的研究成果，而在VRPTW方面的研究则较少，本文在蚁群系统的基础上，将蚂蚁周期算法与最大最小蚂蚁系统（MMAS）相结合，在寻找最优解的过程中采用信息素动态挥发策略；在对下一个客户的选择中，考虑了时间窗跨度及服务等待时间等因素，使问题的解更接近实际情况；通过转移状态规则求得可行节点的概率后，为避免算法陷入局部最优，采用轮盘选择来确定下一点；在求得问题可行解后，为了在不丢失最优解的情况下，更快地产生最优解，采用路径内的2－opt及路径间的2－opt＊优化策略。最后，经过一系列的实验测试验证了改进的蚁群算法对VRPTW的适用性及算法的有效性。

1 问题描述与模型建立

VRPTW的一般定义为:某一配送中心，负责向n个客户点送货，每个客户点i的需求量qi及位置（通常用坐标表示）已知，配送中心派k辆货车进行送货；要求货车必须在其时间窗内为其进行服务，如果配送车辆提前到达，也必须等待，直到时间窗开始为止；每辆货车载重量一定，每条线路上客户点的需求量之和不超过货车车载重量；每辆货车的最大行驶距离一定，每条线路的总长度不能超过货车的最大行驶距离；每个客户的需求必须且只能由一辆货车来提供，目标是使配送的总成本（配送路径总长度和配送车辆数）最小。则该问题的数学模型可写为

式（1）表示费用和所需车辆数最少的目标函数；式（2）表示车辆k运送线路的货物总量不超过车的最大载重量Qk；式（3）表示每辆车从配送中心出发完成配送任务必须回到配送中心；式（4）表示车辆在服务完客户i后直接为客户j服务；式（5）表示车辆在服务j之前只服务一个客户i；式（6）指每个客户i的需求只能由一辆车来满足；式（7）是避免配送过程中产生循环子回路；，为决策变量，当车辆k从点i驶向点j时，＝1，否则＝0，当客户i由的需求由车辆k来完成时，＝1，否则＝0；式（8）可根据时间窗约束的严格与否分为硬时间窗约束和软时间窗约束，本文针对软时间窗约束展开研究。

2 改进的蚁群算法

MMAS对AS的关键改进在于将路径上的信息素浓度限定在 ［τmin，τ］max间，较好地避免了搜索陷入局部最优。由于在搜索过程中，随着信息素的挥发和累计，某些路径上的信息素浓度会远高于其他路径，从而导致了搜索的过早停滞。

2.1 可行路径的构造

在满足容量、路程、时间窗等约束条件下，蚂蚁在选择下一个节点时，需要考虑以下三方面因素:

1）通往下个客户点的路径长度以及当前路径上的信息量；

2）客户时间窗约束因素，由下个客户j的时间窗宽度和所在客户i到达客户j的时间长度等因素决定；选择的原则为需要等待时间较短和时间窗宽度较小时优先选择；

3）基于 Wissner－Gross，A.D.的事物倾向于向自由度较大的方向进化的理论，倾向于选择下一可行节点数多的节点。

令τij为信息素浓度为能见度；dij为顾客i，j之间距离；α为信息启发因子；β为期望启发因子；γ为时间窗跨度的相对重要性；δ为等待时间的影响因子；waitj为开始服务j需要的等待时间，等待时间短的顾客j被选中的概率较大；ETj为顾客j的最最早开始时间，LTj为顾客j的最迟开始时间，则顾客j的时间窗跨度为widthj＝LTj－ETj，根据因素（2）在等待时间相同的条件下，优先选择时间窗跨度较小的节点，时间窗跨度表示了客户的服务紧迫性。

状态转移概率表示蚂蚁k从i点移动到j点的概率，转移规则为

式中:为车辆k从i点出发可访问的所有j（满足容量及时间窗约束且未被访问过的顾客）的集合；r为在 ［0，1］上服从均匀分布的随机变量；r0（0≤r0≤1）为用来控制转移规则的参数；当r≤r0时，算法采用确定性搜索，此时蚂蚁以概率r0选择距离较短的路径；当r＞r0时，算法采用探索性搜索，此时蚂蚁以概率1－r0随机选择路径。为了加快构造初始解，在算法迭代的初期r0选取较大的初始值，以较大的概率进行确定性搜索；在算法的中期r0选取较小的值，增大探索性搜索的概率，这样可以扩大搜索空间，有效防止算法停滞，陷入局部最优解，在算法的后期恢复r0的初始值，加快算法收敛速度。

2.2 算法步骤

Step1:初始化。置迭代步数nc＝0，初始化各个参数，读取客户数据，将所有蚂蚁放在配送中心；

Step2:令一蚂蚁从配送中心出发，让每只蚂蚁按转移规则（11）选择下一访问点j，同时更新禁忌表，将新的客户点加入到该“蚂蚁”的禁忌表中；

Step3:判断禁忌表的状况，如果还有未访问的顾客点，转Step2，否则表示第k只蚂蚁完成迭代，执行Step4；

Step4:计算并保存禁忌表中第k只蚂蚁所经过的客户节点和总路径长度len（k）；

Step5:更新信息素，并将信息素限定在 ［τmin，τmax］，增加蚂蚁搜索路径的随机性。

Step6:计算m只蚂蚁中所经过的路径长度并计算出最短路径，采用路径内的2－opt及路径间的2－opt＊优化策略，找出当前最优解；

Step7:若nc≤max＿nc，则nc＝nc＋1，清空记录表，转Step2，否则，流程结束。

3 实验结果与分析

选用需求点为25个的数据集，其中配送中心的编号为0，坐标为（35km，35km），其他客户属性如表1所示。

表1 客户需求信息表

本文采用MATLAB7.8.0对模型进行求解，试验中客户数是蚂蚁数的1.5倍，信息启发因子α＝1，期望启发因子β＝2，γ＝1.5，δ＝2，信息素残留因子ρ＝0.9，迭代次数nc＝1 000，配送货物的货车类型有三种，其载重容量分别为6t，7t，8t，对应的行驶速度分别为45km／h，40km／h，35km／h，最大行驶距离为150km，180km，200km。对于同一数据集，分别选用不同的车辆类型对此问题进行求解，结果如表2所示。

表2 实验结果

从表2可以看出，对于同一数据集，随着车辆载重量的增加，配送车辆数逐渐减少，由于每辆配送车在完成配送任务后，均要回到配送中心，从而总路径长度也会相应缩短，但考虑到大容量车辆的大能耗，反而会增加配送成本，最后选取一个折中的派送方案——混合车型，从表2可以看出，在配送车辆数不变的情况小，可以得到一个满意解，在实际的配送任务中，考虑到小车型的快捷性、低能耗及人们对配送的及时性要求越来越高，多车型组合的配送方案将在很大程度上提高服务质量，降低配送成本。

为了更清楚地表示出运行结果，图1、图2、图3分别为车型为6t和混合车型的运行结果路径图和进化图。

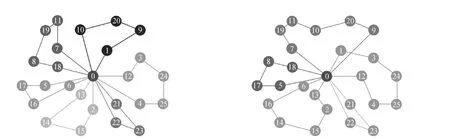
图1 车型为6t和混合车型配送方案

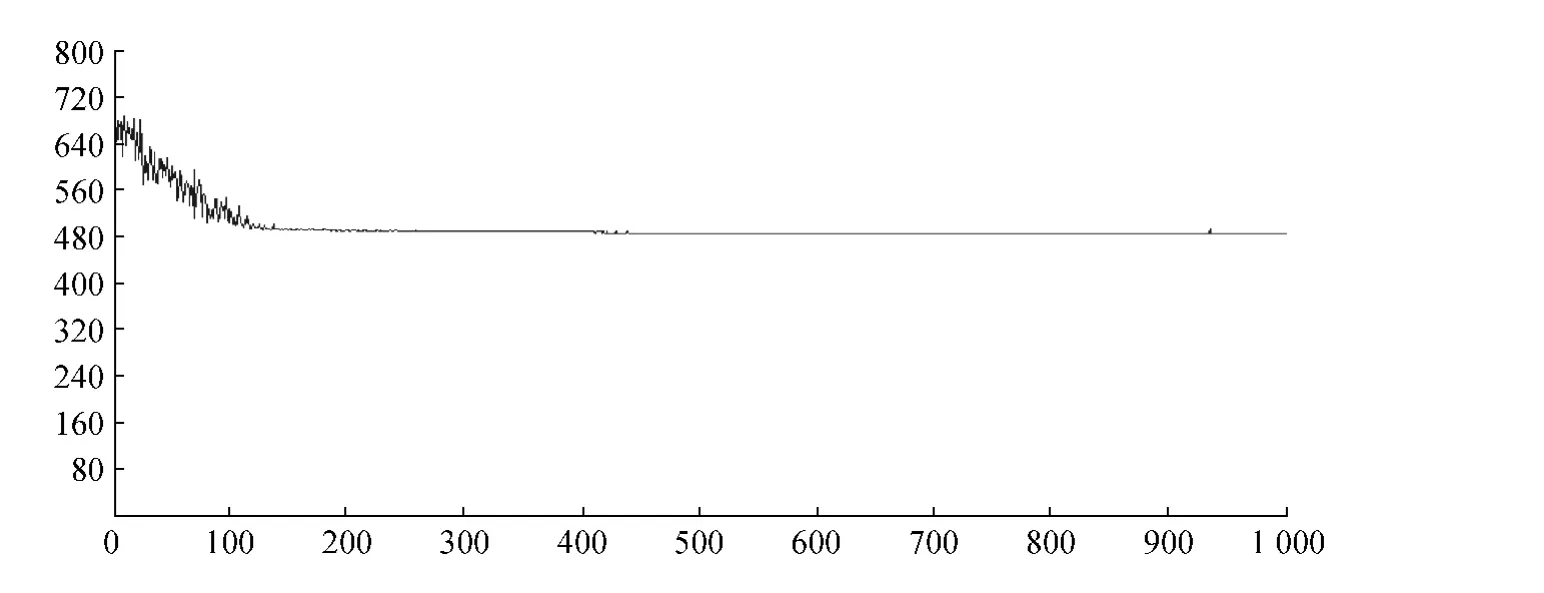
图2 车型为6t进化

图3 混合车型进化

从图2和图3的程序进化图可以看出，当车型为6t时，在算法迭代到100次时算法已趋于收敛，表明本文提供的算法能快速准确地求出带时间窗约束的车辆路径问题的最优解，而对于混合车型，在算法迭代到300次时求得的最优解仍有波动，这是因为在确定配送方案时还需要考虑车型对目标的影响，增加了算法复杂度，这也验证了在时间窗约束的基础上增加多车型这一约束时算法将会变得更加复杂。

4 结束语

本文针对多车型的带软时间窗约束的车辆路径问题展开研究，以配送车辆总行驶距离和车辆数最小化为优化目标，建立了该问题的数学模型，并设计了改进的最大最小蚁群算法对该数学模型进行求解。最后结合算例实验基于多车型的带软时间窗的车辆路径进行验证，结果显示可以有效减少配送成本，证实了算法的有效性和选用多车型方案的科学性。

［1］ Mester D，Bräysy O.Active guided evolution strategies for large－scale vehicle routing problems with time windows［J］.Computers ＆ Operations Research，2005，32（6）:1593－1614.

［2］ 王建玲，齐紫茜，何璐.基于蚁群算法的车辆调度问题［J］.交通科技与经济，2014，16（6）:37－39.

［3］ M D，V M，A C.Ant System:Optimization By A Colony Of Cooperating Agents［J］.IEEE Trans Syst Man Cybern B Cybern，1996，26（1）:29－41.

［4］ Demirel N，Duran Toksarı M.Optimization of the quadratic assignment problem using an ant colony algorithm［J］.Applied Mathematics ＆ Computation，2006，183（1）:427－435.

［5］ Ellabib I，Calamai P，Basir O.Exchange strategies for multiple ant colony system ［C］.／／Information Sciences，2007:1248－1264.

［6］ Stützle T，Hoos H.Improvements on the Ant－System:Introducing the MAX－MIN Ant System［J］.Artificial Neural Nets ＆ Genetic Algorithms，1997.

［7］ 万旭，林健良，杨晓伟.改进的最大－最小蚂蚁算法在有时间窗车辆路径问题中的应用［J］.计算机集成制造系统，2005，11（4）:572－576.

［8］ AD W，CE.F.Causal Entropic Forces［J］.Physical Review Letters，2013，110（16）:1－5.