分布式MIMO系统线形小区天线位置优化研究

付明浩，李岳衡

分布式MIMO系统线形小区天线位置优化研究

付明浩，李岳衡

对于研究分布式MIMO（Multiple-Input Multiple-Output）系统线形小区基站侧天线端口的位置优化问题具有很重要的现实意义。以最大化小区平均遍历容量为目标函数，研究了分布式MIMO系统中基站侧天线位置的最优分布问题。根据仿真结果可得出如下结论：基于粒子群智能优化算法的次优搜索可以有效解决该类优化问题；对天线最优位置产生影响的主要因素包括：用户位置的分布、基站天线的布局方式以及基站侧天线端口的数目等。

分布式MIMO；粒子群算法；平均遍历容量；天线位置优化

0 引言

现实生活中，无线通信系统的建模会综合考虑到人们的生活需求和所处地理环境的影响，常见的系统模型有蜂窝状的六边形小区，也有圆形、三角形以及线形小区。当身处笔直的街道、河流、铁路和高速公路时，移动终端近似可以看成只在直线范围内活动，通常这类小区都被建模成线形小区。

考虑一个线形小区分布式MIMO系统，如图1所示：

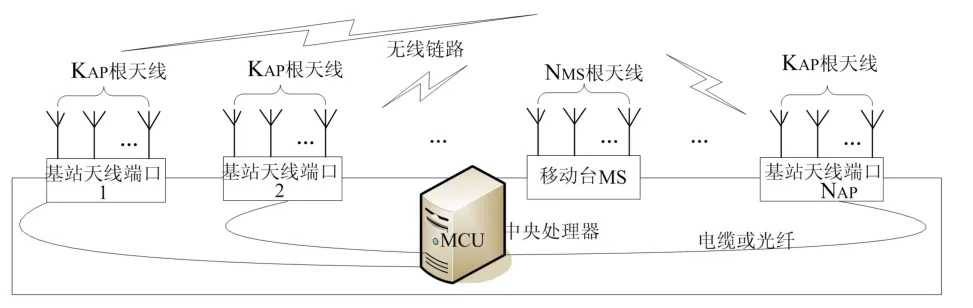
图1 线形小区分布式MIMO系统(NAP,KAP,NMS)

NAP个天线端口AP分散放置在线形小区内，每个AP配置有KAP根天线，移动终端MS则配置有NMS根天线，记为系统。考虑下行通信链路，即AP侧为信号发射端，MS侧为信号接收端。

本文将着重研究分布式MIMO系统在线形小区中基站侧天线端口位置的分布问题。在分布式MIMO系统中，基站侧天线的位置分布直接影响着通信系统的各项性能[1]-[2]，不同的位置分布会对系统的平均误比特率和平均遍历容量等产生很大的影响[3]。生活中不乏线形小区的例子，比如繁华的街道、笔直的高速公路等都可以建模成线形结构的小区，因此，对于线形小区中基站侧天线位置分布的研究具有很重要的现实意义。

1 系统模型

本文关于线形小区中天线位置分布的研究采用的系统模型可简化如图2所示：

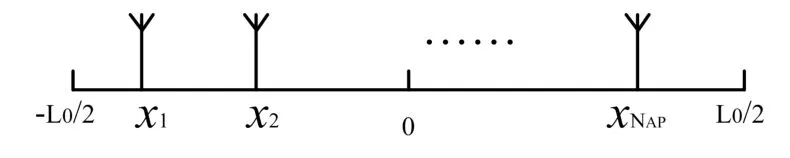
图2 线形小区中天线位置分布示意图

在长度为L0的线形小区中，假设小区中心处坐标为0，NAP个天线端口AP依次分布在线形小区中，位于小区中不同的地理位置处，为方便统计，假设第i(1≤i≤NAP)个 AP的坐标记为xi，并且有x1＜x2＜…＜xNAP；每个AP配置有KAP根天线；移动终端MS配置有NMS根天线，且在整个线形小区中均匀分布。

考虑如下建模，假设无线信号经历的是复合衰落信道，即充分考虑了阴影效应、路径损耗以及快衰落对无线信道的影响，其中快衰落采用了常见的Rayleigh衰落模型；考虑下行通信链路；发射天线采用等功率分配方案。

2 优化问题的提出

本文的研究内容是以最大化小区平均遍历容量为目标函数来寻求天线位置的最优解[4]，该优化问题的数学模型如公式（1）：

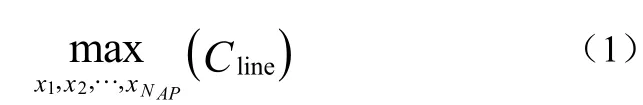
式中，x1,x2,…,xNAP分别表示各个天线端口的位置，那么小区平均遍历容量取得最大值时各个天线端口的位置p1,p2,…,pNAP即为该优化问题的解如公式（2）：

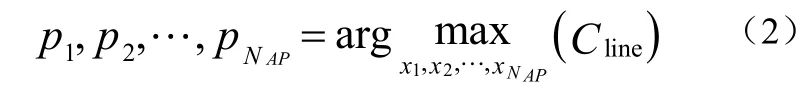
当用户的位置u在线形小区中服从均匀分布时，其概率密度函数如公式（3）：

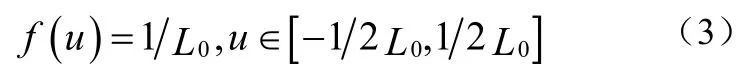
那么由下行链路遍历容量的表达式式可知公式（4）：

由矩阵的性质，可知公式（5）：

上式中，由于快衰落矩阵R以及阴影效应S均不是天线位置的函数，同时调换式(4)中Eu和EL，S，R的顺序，那么得到公式（6）、（7）：

此时，该优化问题就转化为求遍历容量下界的最大值问题，注意此时求得的为次优位置，那么优化问题的解可以转化为下式的求解得公式（8）：

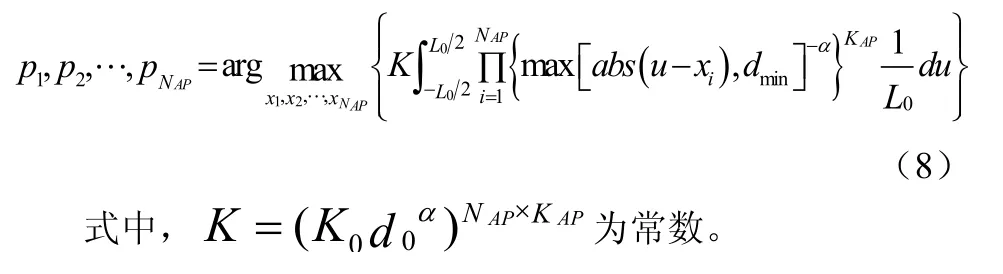
3 粒子群优化算法求解优化问题

用粒子群优化算法（PSO）求解小区中天线位置的分布问题时，基站侧天线处于一维空间中，那么对应优化问题的搜索区域即为一维空间，此时，各个粒子的位置、速度以及个体最优解均可以用一个实数来表示，粒子的适应度即为天线端口分布于粒子所在位置时的小区平均遍历容量Cline。根据PSO算法流程，得出求解该优化问题的步骤如下：

STEP1：初始化粒子群。假设搜索区域内粒子的个数为M，那么需要初始化M个粒子的位置信息、速度信息以及初始的个体最优解初始化迭代次数N=0；并设置迭代次数的门限值N0、学习因子c1和c2、惯性系数λ的值。此外，还需要设置粒子运动的速度上限vmax，限制粒子的速度在区间中，以免速度值过大，导致粒子陷入局部最优解。

STEP2：计算M个粒子的初始适应度。根据线形小区平均遍历容量的表达式，结合各个粒子的位置信息，计算适应度Si，并找出适应度最大的粒子，作为初始的全局最优解Gbest0。

STEP3：更新粒子的位置和速度。假设上一次的迭代次数为k，那么第i(1≤i≤M)个粒子经过k+1次迭代之后的位置和速度可以按照下式进行更新为公式（9）：

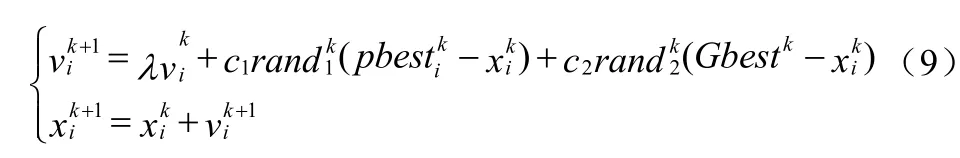
更新完速度和位置之后，需要判断该粒子是否还在搜索区域内，若已经超出了该区域，那么需要重新更新粒子，重复STEP3。

STEP5：重复STEP3～STEP4，直到迭代次数k达到门限值N0，满足算法的收敛准则，输出全局最优解Gbest，即优化问题的次优解。

4 仿真与分析

本节主要利用粒子群优化算法求解线形小区中天线位置的最优分布问题[5]，并验证该算法的有效性，同时通过各种场景的模拟，研究线形小区中天线位置对小区平均遍历容量的影响以及系统中各参数对天线最优位置的影响，主要仿真参数，如表1所示：

表1 线形小区仿真参数列表

用粒子群算法求解线形小区中AP位置的最优分布时，首先需要对粒子群体进行初始化。如图3所示：

图3 线形小区中粒子群体的初始位置

为一维搜索空间域中粒子群体的初始位置，粒子随机分布在直线区间[-1000,1000]中。

在搜寻最优解的过程中，粒子的位置不断的更新，经过一定次数的迭代后，粒子群体会收敛在最优解区域。如图4所示：

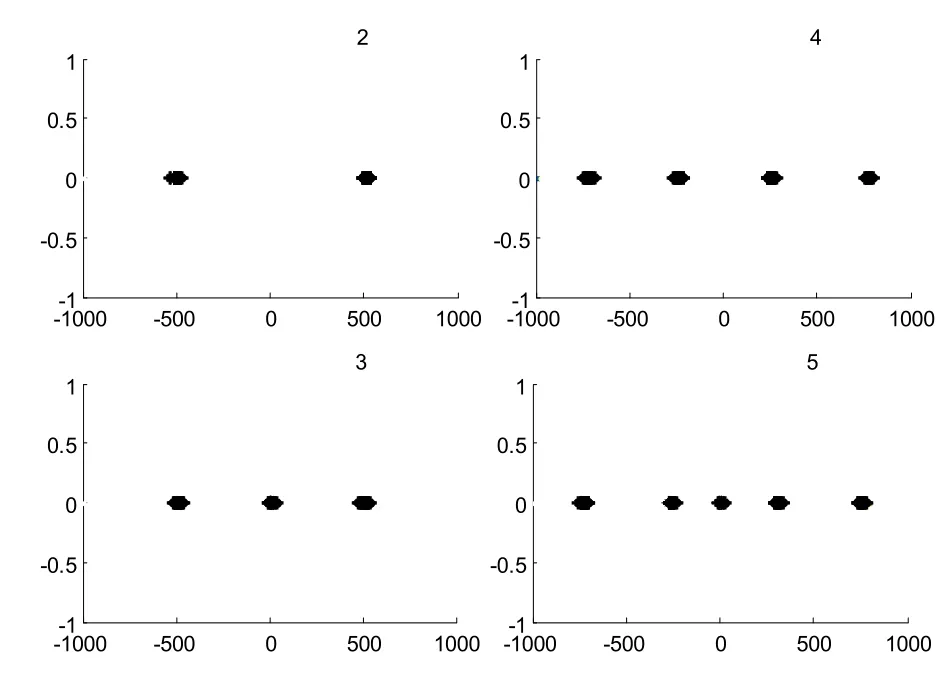
图4 线形小区中基于粒子群算法的次优搜索

为线形小区中AP数目分别为2,3,4,5时对应优化问题的次优解，图中粒子高度聚集的位置即为天线分布的最优解区域，全局最优解的位置即为粒子群搜索到的次优解，即天线的次优位置。从仿真结果可以看出，当AP数目为偶数时，所有的AP均分布在关于小区中心两两对称的位置；若为奇数时，有一个AP放置在小区中心位置，其余AP均分布在关于小区中心两两对称的位置。

仿真结果显示了天线位置分布对线形小区平均遍历容量的影响，充分说明了小区平均遍历容量会随着天线位置的变化而发生变化，进一步肯定了研究线形小区中天线位置分布的必要性如图5所示：

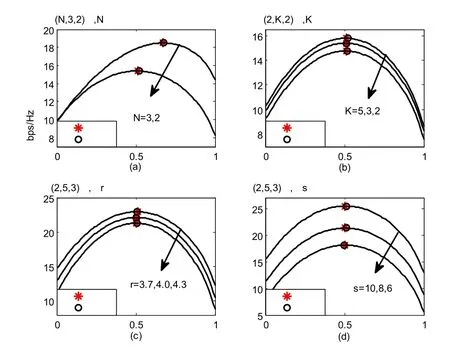
图5 线形小区遍历容量与天线位置的关系

图5中，坐标原点（0,0）表示线形小区的中心位置，仿真中主要考虑了天线端口数目N分别为2和3两种场景，当N=2时，两个AP关于小区中心对称放置；当N=3时，其中一个AP置于中心处，其余两个AP关于小区中心对称放置。图中天线的最优位置是通过计算机搜索得到，次优位置由粒子群算法搜索得到，观察发现，由粒子群算法得到的次优位置可以很好地逼近最优位置，能有效解决该优化问题。

其中，(a)图展示了同一位置处，天线端口数目N对小区平均遍历容量的影响，遍历容量随着N的增大而提高；同时从图中可以看出，N为2时，小区平均遍历容量大约在归一化距离为0.5时达到最大；N为3，天线分布的最优位置开始向小区边缘偏离。

(b)图中，固定了天线端口数目和用户端的天线数目，即研究了（2，K，2）系统中K对小区平均遍历容量的影响，其中K表示每个天线端口安装的天线数目，观察小区平均遍历容量的变化曲线可以发现，随着K的增加，小区平均遍历容量随之而增加；同时，当K的取值不同时，天线分布的最优位置始终保持不变，其归一化距离始终维持在0.5左右，这是因为K的取值并不影响基站天线与用户天线的平均接入距离。关于用户端天线数目对天线最优位置的影响与K值对系统性能的影响极其相似，为避免赘述，便没有给出仿真结果。

(c)图和(d)图中，分别研究了（2,5,3）系统中，在不同信道参数下，天线位置对线形小区平均遍历容量的影响。从(c)图中可以看出，当天线端口处于同一位置时，小区平均遍历容量随着路径衰落指数的增加而下降，这是因为，随着路径衰落指数的增加，系统中的路径损耗逐渐增强，从而导致接收端信噪比的下降，那么根据香农定理，系统的遍历容量也会随之而降低。

观察(d)图可以发现，当天线端口固定于某一位置时，小区平均遍历容量会随着阴影效应标准差的增加而提高，与(b)图类似，当各信道参数取值不同时，天线分布的最优位置大致保持不变，从一定程度上说明了信道参数并不是影响基站侧天线端口位置最优分布的主要因素。

5 总结

本文主要基于粒子群智能优化算法研究了线形小区中基站侧天线位置的最优分布问题。为此首先介绍了线形小区的系统模型，在此基础上，以最大化小区平均遍历容量为目标函数，将粒子群算法运用到求解线形小区天线位置优化问题的过程中。仿真结果表明：基于粒子群优化算法搜索得到的次优位置能够很好地逼近天线分布的最优位置，其误差能够控制在一定范围以内；并且相对于计算机搜索，粒子群搜索可以大大降低计算的复杂度，能够有效解决天线位置的分布问题。此外，综合线形小区仿真结果还可以得出结论：影响天线最优位置的主要因素是基站侧天线端口数目、天线布局方式以及用户位置分布等三大系统参数。

[1]Wang X, Zhu P, Chen M. Antenna location design forgeneralized distributed antenna systems[J].Communications Letters, IEEE, 2009, 13(5): 315-317.

[2]韩亮,柳鑫,唐友喜等.线型小区中V-BLAST两根分布发射天线的位置优化[J].电子与信息学报,2010,32(4): 978-982.

[3]Shen Y,Tang Y,Kong T,et al.Optimal antenna location for STBC-OFDM downlink with distributed transmit antennas in linear cells[J].Communications Letters,IEEE,2007,11(5):387-389.

[4]Firouzabadi S, Goldsmith A. Optimal placement ofdistributed antennas in cellular systems[C].SignalProcessing Advances in Wireless Communications(SPAWC), 2011 IEEE 12th International Workshop on.IEEE, 2011: 461-465.

[5]郑娜娥,王大鸣,崔维嘉.一种分布式MIMO系统的快速天线选择算法[J].计算机工程与应用,2011,47(22): 99-101.

Antenna Port Placement Optimization of Distributed MIMO System in Linear Cell

Fu Minghao,Li Yueheng
(College of Computer and Information,Hohai University,Nanjing,211100,China)

The research on the antenna port(AP)placement optimization of distributed multiple-input multiple-output(DMIMO) system in a linear cell has a very important practical significance.It discusses the optimal placement problem of base station antennas in DMIMO systems to maximize the cell average ergodic capacity.In the light of simulation results,it can be concluded that:the search based on Particle Swarm Optimization(PSO)can solve the optimization problem effectively.On the other hand,the main factors that affect the optimal antenna location include:the distribution of the user's location,the layout of the base station antennas and the number of antenna ports,and so on.

Distributed Multiple-Input Multiple-Output;Particle Swarm Optimization;Average Ergodic Capacity;Antenna Port Placement Optimization

TP311

A

1007-757X(2015)06-0032-03

2015.01.16）

付明浩（1991-），河海大学，计算机与信息学院，硕士研究生，研究方向：现代无线通信网络、MIMO系统，南京，211100

李岳衡（1971-），河海大学，计算机与信息学院，教授，博士，研究方向：移动通信中的多天线传输理论与技术、现代无线传感网络协同信息获取与处理，南京，211100