高斯加权的重构性K-NN算法研究

刘作国，陈笑蓉

(贵州大学 计算机科学与技术学院，贵州 贵阳 550025)



高斯加权的重构性K-NN算法研究

刘作国，陈笑蓉

(贵州大学 计算机科学与技术学院，贵州 贵阳 550025)

该文提出基于高斯加权距离以及聚类重构机制的K-NN文本聚类算法。文章提出K-NN近邻域的概念，通过高斯加权的近邻域算法实施K-NN聚类。利用高斯函数根据样本与聚类中心的距离为样本赋权，计算聚类距离。基于近邻域权重和聚类密度对形成的聚类实施重构，实现聚类数目的自适应调整。使用拆分算子拆分稀疏聚类并调整异常样本；使用合并算子合并相似聚类。实验显示聚类重构机制能够有效地提高聚类的准确率及召回率，增加聚类密度，使得形成的聚类结果更加合理。

文本聚类；K-NN算法；高斯加权；近邻域规则；聚类重构

1 引言

K-NN聚类算法简洁实用，是一类常见的文本聚类算法。K-NN算法选定样本子集形成初始聚类分布，根据初始分布将测试样本划入最近聚类。K-NN算法初始聚类的选择直接影响聚类结果，聚类过程缺少对结果的检测和调整机制，难以实现聚类数目的自适应变更[1]。

本文主要针对K-NN算法的距离判定策略和聚类重构机制进行了研究，通过高斯加权算法实施距离度量，判定样本归属。采用聚类重构机制对不合理聚类实施拆分及合并，实现聚类数目的自适应调整，同时保证形成的聚类更加紧密合理。

2 相关工作

2.1 文本表示

本文主要采用向量空间模型VSM进行文本描述，文本t表示为式(1)。

(1)

同时采用欧式距离描述文本a,b之间的关系，如式(2)所示。

(2)

2.2 聚类密度

本文使用几何中心来定义聚类的中心，并通过聚类密度描述聚类内样本的相关性。

定义1(聚类中心) 聚类C的中心定义为其几何中心:

(3)

定义2(聚类密度) 聚类C的密度定义为式(4)。

(4)

聚类内部样本与聚类中心越接近，聚类密度就越高，重构的必要性就越小。优先选择密度较低的聚类实施重构可以提高聚类效率。

2.3 簇间距离

文献[2]认为样本的空间分布具有正态分布的性质，靠近聚类中心的样本权重较高，对聚类间距的影响较大。本文参考其思想，设计了一种高斯加权算法来计算聚类间距，使算法向聚类中心的高密度区域靠近。

定义3(簇间距离) 样本x相对于聚类C的高斯权重为:

(5)

样本x与聚类C的距离为:

(6)

聚类Ci与Cj的距离为:

(7)

为便于计算，式(5)取μ=K(C),σ=1。

3 加权K-NN聚类算法

K-NN聚类是一类常用的文本处理算法。算法的思想是: 如果一个样本S的K个最近邻更靠近聚类C，就将S划分入聚类C。

K-NN聚类思想建立在理想假设下，要求初始状态的聚类划分合理，并且已经形成的每个聚类内部联系紧密。但实际情况往往并非如此，即便初始聚类划分是理想的，随着大量样本不断加入聚类，聚类内部的关联性可能降低，导致形成的聚类偏离理想状态[3-4]。

3.1 邻近域

假设K-NN聚类算法取K=3，图1中待测样本x(以圆形表示)被划分入聚类b(以三角形表示)。但实际上聚类b密度较低，b类样本之间距离较大，两个相近样本距离聚类b中心较远，因此样本x距离聚类a(以方形表示)比较近。出现以上问题的原因在于K-NN聚类没有考虑两个聚类中的样本对待测样本x的影响力，换而言之没有考虑两个聚类中各个样本的权重。

图1 近邻域权重的意义

文献[5]提出一种文本的权重量化思想，指出文本分布越密集的样本空间区域对聚类划分的影响越高。文献[6-7]提出距离聚类中心越近的样本对聚类的表征能力越强，因此权重也越高。

借鉴经典的K-NN聚类思想，本文提出加权近邻域的概念来处理待测样本的划分问题，并且认为越靠近聚类中心的样本对聚类的影响力越高，样本权重也越大[8]。

定义4(近邻域) 与样本x距离小于d的全部样本构成x的d近邻域，记为式(8)。

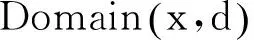
(8)

其中d称为近邻域的半径。

定义5(近邻域权重): 样本x的d近邻域为Domain(x,d)，聚类Ci与Domain(x,d)交集为Si=Domain(x,d)∩Ci，则:

(9)

称为x在Ci上的d近邻域权重，在不引起混淆的情况下简称为x的权重。

3.2 近邻域规则

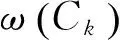
选取近邻域半径d内的K个(d为确定值，K为不确定数目)相邻对象进行聚类判定。采用近邻域规则判定待测样本x的类别划分: 样本划分入K个邻近对象最接近的聚类。其中d为样本S到最近的聚类的距离。

3.3 聚类重构

为解决初始聚类对聚类结果的影响，采取聚类重构策略对获得的聚类实施重构。

聚类重构机制根据聚类的密度及各样本的距离拆分稀疏的聚类，合并相近聚类从而实现聚类的数目及空间分布的自适应调整。重构机制需要考虑以下情形:

1) 异常样本调整。若聚类内少数样本与簇内其他样本联系较弱，应当将这些“另类”样本调整到其他聚类中；

2) 稀疏聚类拆分。若聚类密度过低，说明簇内样本分布稀疏，应当将稀疏聚类拆分为多个密集聚类；

3) 相似聚类合并。若多个聚类联系紧密，考虑将它们合并为一个聚类，合并后可能需要考虑1)、2)类问题。

1)类问题采用近邻域算法处理；2)、3)两类问题分别采用拆分算子和合并算子进行处理。聚类过于稀疏不利于判断聚类间距，会影响聚类合并，因此聚类重构应当先拆分后合并，并优先处理密度低的聚类[9]。本文参照文献[10]阐述的聚类改进策略，设置密度阈值来限定拆分算子的作用范围，聚类拆分的算法如下:

聚类拆分算法

Step1 在密度低于阈值的聚类中选择密度最低的聚类Ci;

Step2 获取簇内任意未处理成员t;

Step3 寻找t最近聚类Cj;

Step4 若Ci=Cj转Step6，否则继续:

① 若exp[-D(t,Cj)]≥Den(Cj)，t归入Cj;

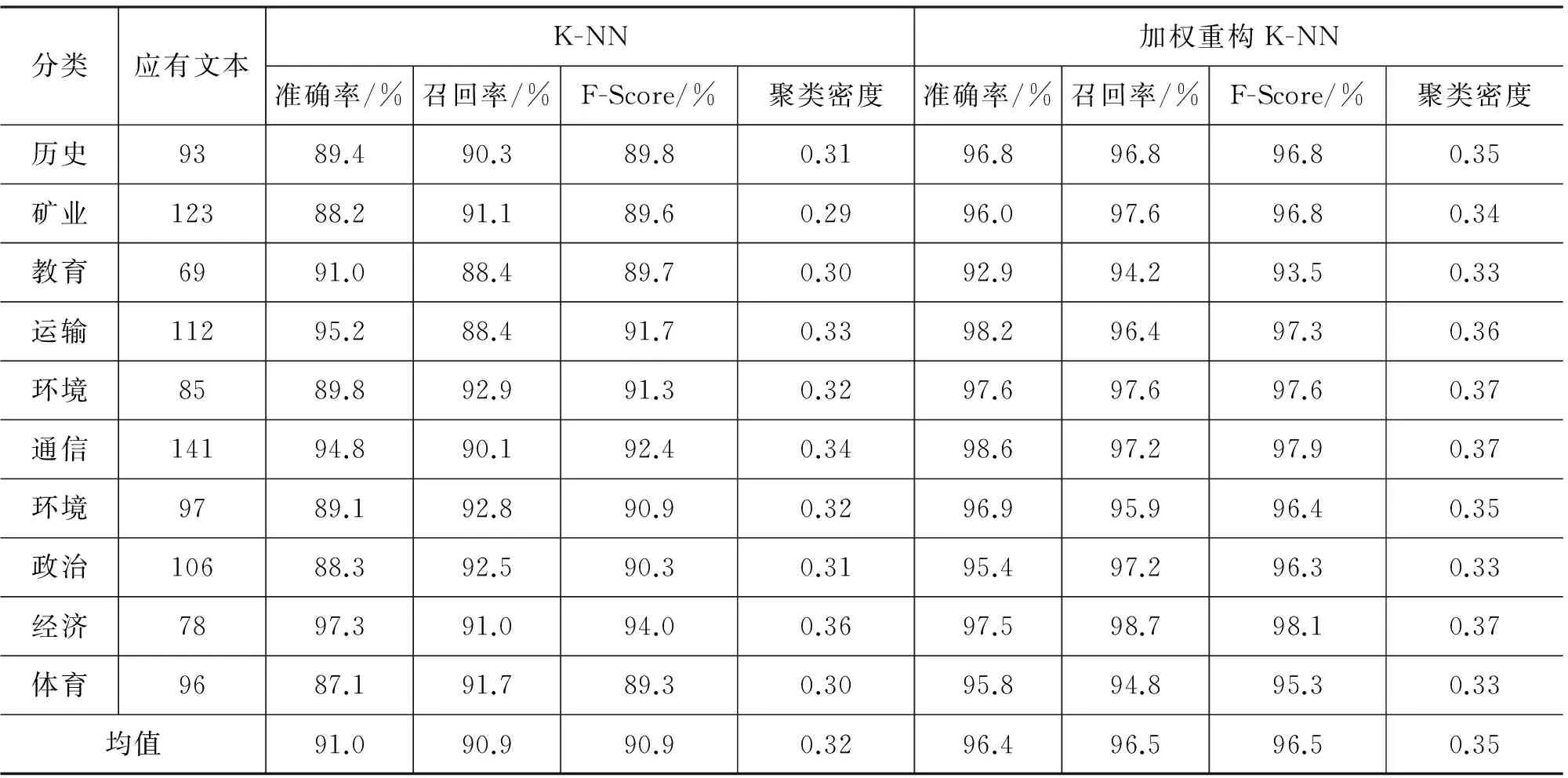
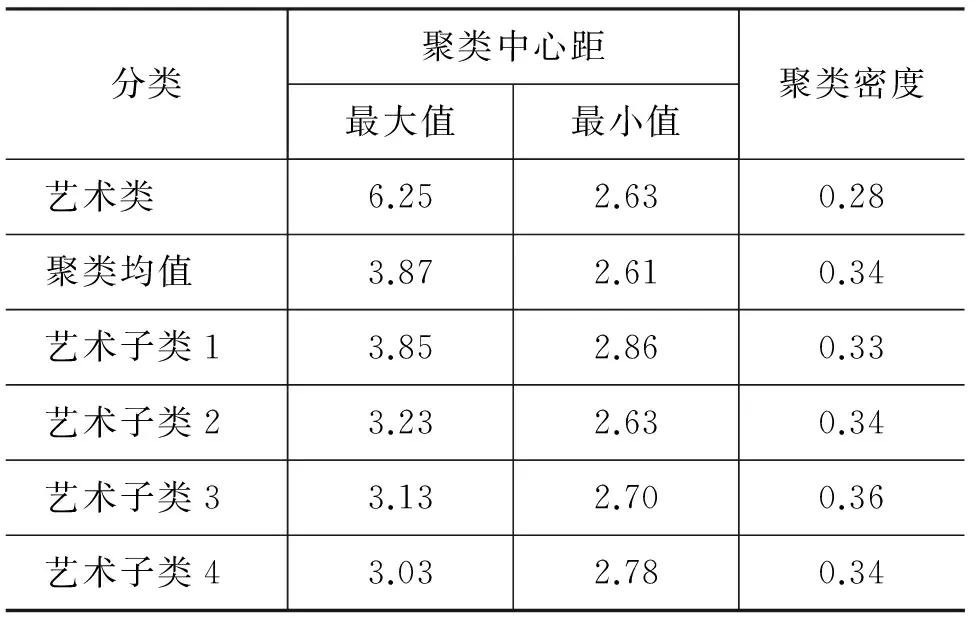
② 若exp[-D(t,Cj)]

Step5 更新聚类中心及聚类密度；

Step6 迭代处理聚类Ci内所有样本。

算法Step4中，样本t最近聚类为Cj，若exp[-D(t,Cj)]≥Den(Cj)，说明t比Cj中大多数样本都更接近聚类中心，允许将t归入Cj;反之说明t距离Cj中心较远，进而断定没有与t相近的聚类，需要新建聚类来容纳样本t。

设样本规模为n，理论上拆分算子完成所有计算的平均复杂度为O(n2)，由于聚类中心、聚类密度、高斯权重等复杂计算在聚类过程中已经完成，拆分算子实际时间开销为O(n×logn)。

聚类合并的算法如下:

聚类合并算法

Step1 整个聚类集添加到未处理聚类集合Cu;

Step2 获取任意未处理聚类Ci;

Step3 寻找Ci最近聚类Cj;

Step4 分析Ci与Cj关系:

若exp[-D(Ci,Cj)]≥Den(Ci)或exp[-D(Ci,Cj)]≥Den(Cj)，合并聚类Ci与Cj，更新聚类中心及密度，将新聚类添加到Cu。否则不予以合并；

Step5Cu中删除已处理聚类；

Step6 迭代处理Cu中所有聚类。

算法Step4中，若exp[-D(Ci,Cj)]大于等于Ci或Cj任意一个的聚类密度，说明两个聚类存在较大交集，二者具有包含或较大的重叠关系，考虑将两个聚类合并。合并产生的新聚类仍作为未处理聚类参与迭代过程。

理论上合并算子复杂度为O(n2)，实际为O(n×logn)。

重构机制示例 假设样本空间共包括三类16个文本，用三种图形各代表一类文本。初始状态文本集被分为四类，星形表示各聚类几何中心，箭头指向文本的最近聚类。理想状态重构过程如图2所示。

图2 聚类重构示例

经过聚类重构，稀疏聚类得到优化，初始状态对聚类结果的影响也被削弱。聚类的拆分及合并使得聚类数目动态调整，无需用户干预，更符合聚类处理的实际应用需求。

4 实验分析

本文从复旦大学中文语料库分别随机选取500和1 000个样本进行聚类实验。采用K-NN算法和加权重构K-NN模型分别进行聚类。统计各类别的准确率、召回率、F-Score值并计算获得的聚类密度。

实验结果显示近邻域算法和聚类重构机制对文本聚类的处理是有效的。经过重构处理后各类文本准确率、召回率均有显著提升，聚类密度有所提高，说明重构之后聚类内部样本关联性更强。

表1 500样本K-NN聚类及加权重构K-NN结果对比

表2 1 000样本K-NN聚类及加权重构结果K-NN对比

从表1及表2可见，艺术类准确率、召回率及聚类密度较低，这是由于语料库对文本的人工标注不够细致。语料库艺术类包括音乐、书画、舞蹈、美学等多个领域的文章，虽然这些领域都属于“艺术”范畴，但文本的词汇特征相差甚远。通过聚类重构，“艺术”类被划分为四个子类，如表3所示，每个子类密度仍然是可接受的。

表3 “艺术”子类

表1与表2的对比结果显示，不同样本规模下准确率、召回率有一定差别，但重构后聚类密度却相差无几，这说明聚类算法对样本规模是敏感的，但重构机制不受到样本规模的影响。

5 总结

本文提出一种高斯加权的K-NN文本聚类算法。采用高斯函数对初始聚类中各个样本的影响力进行评估。文章引入聚类重构机制调整稀疏聚类，能够有效提高聚类密度并实现聚类数目的自适应调整。实验表明，重构机制不受到样本规模和初始划分的影响，能够有效地提高聚类精度，保证聚类的紧密性，其算法时间开销在可接受范围。

本文在近邻域的加权规则和距离度量方面还存在改进和优化的空间。更合理的近邻域加权规则可以使得K-NN聚类所获得的聚类更加合理，同时也有助于对稀疏聚类的判定，减小聚类重构的代价。

[1] Hyeong-Il Kim and Jae-Woo Chang. K-Nearest Neighbor Query Processing Algorithms for a Query Region in Road Networks[J]. Journal of Computer Science & Technology, 2013, 28(4): 585-596.

[2] 刘金岭,冯万利,张亚红.初始化簇类中心和重构标度函数的文本聚类[J].计算机应用研究,2011,28(11): 4115-4117.

[3] 王灿田,孙玉宝,刘青山.基于稀疏重构的超图谱聚类方法[J].计算机科学,2014,41(2): 145-148,156.

[4] 曾依灵,许洪波,吴高巍,等.一种基于空间映射及尺度变换的聚类框架[J].中文信息学报,2010,24(3): 81-88.

[5] Amineh Amini, Teh Ying Wah, Mahmoud Reza Saybani, et al. A Study of Density-Grid based Clustering Algorithms on Data Streams[C]//Proceedings of the FSKD 2011. Shanghai China. 2011: 1652-1656.

[6] 陈建超,胡桂武,杨志华,等.基于全局性确定聚类中心的文本聚类[J].计算机工程与应用,2011,47(10): 147-150.

[7] 季铎,王智超,蔡东风,等.基于全局性确定聚类中心的文本聚类[J].中文信息学报,2008,22(3): 50-55.

[8] 王骏,王士同,邓赵红. 特征加权距离与软子空间学习相结合的文本聚类新方法[J].计算机学报,2012,35(8): 1655-1665.

[9] M Shahriar Hossain, Praveen Kumar Reddy Ojili, Cindy Grimm, etal. Scatter/Gather Clustering: Flexibly Incorporating User Feedback to Steer Clustering Results[J]. IEEE Transactions on Visualization and Computer Graphics, 2012, 18(12): 2829-2838.

[10] NishaM N, Mohanavalli S, Swathika R. Improving the quality of Clustering using Cluster Ensembles[C]//Proceedings of 2013 IEEE Conference on Information and Communication Technologies. 2013: 88-92.

Research on Gauss Weighed Reorganization K-NN

LIU Zuoguo, CHEN Xiaorong

(College of Computer Science & Technology Guizhou University, Guiyang,Guizhou 550025, China)

This paper presents a K-NN text clustering algorithm employing uses Gauss Weighed Distance and Cluster Reorganization Mechanism. The concept of Nearest Domain is proposed and Nearest Domain Rules are elaborated. Then Gauss Weighing Algorithm is designed to Quantification samples’ distance and weights. A text is weighed based on the distance from cluster center via Gauss function in order that distances of clusters can be calculated. Further, Cluster Reorganization Mechanism will make a self-adaption to the amount of clusters. Splitting operator separates sparse clusters and adjusts abnormal texts while consolidating operator combines similar ones. Clustering experiment shows that reorganization process effectively improves the accuracy and recall rate and makes result more reasonable by increasing the inner density of clusters.

text clustering; K-NN; Gauss weighing; nearest domain rule; cluster reorganization

刘作国(1987—),博士研究生,主要研究领域为中文信息处理。E-mail:412769371@qq.com陈笑蓉(1954—),教授,主要研究领域为中文信息处理。E-mail:xrchengz@163.com

1003-0077(2015)05-0112-05

2015-07-31 定稿日期： 2015-09-07

国家自然科学基金(61363028)

TP391

A