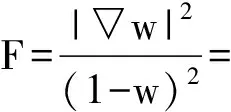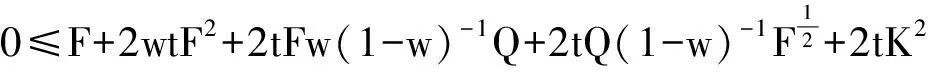紧致流形上非齐次热方程的椭圆型梯度估计
谢 飞
(南通师范高等专科学校,江苏如皋 226500)
紧致流形上非齐次热方程的椭圆型梯度估计
谢 飞
(南通师范高等专科学校,江苏如皋 226500)
本文借助于加权Bochner公式以及极大值原理,在紧致流形上讨论非齐次加权线性热方程(∂t-Δf)u=A(x,t)正解的椭圆型梯度估计,这里A(x,t)是定义在M×[0,+∞)上的光滑函数。
紧致流形;椭圆型梯度估计
1 提出问题
P.Li和S.T.Yau得到了关于线性热方程[1]
(∂t-Δ)u=0.
(1.1)
正解的抛物型梯度估计,由该估计得到的Harnack不等式只能用来比较在不同时刻流形上不同点处正解的值.为了比较同一时刻流形上不同点处正解的值,需要建立关于线性热方程的椭圆型梯度估计.
本文在紧致流形上讨论非齐次加权线性热方程
(∂t-Δf)u=A(x,t).
(1.2)
正解的椭圆型梯度估计,得到了以下结论.
定理 (M,g)是一个n维紧致无边黎曼流形,dμ=e-f(x)dx是M上的加权测度,其中f是光滑势函数,假设
Ricf≥-K2.
(1.3)
其中,K≥0为常数.如果u>0为(1.2)的正解,满足
0 (1.4) 且对某个Q>0为常数,有 (1.5) 则对于任意的x∈M,t>0, (1.6) 其中C>0为常数. 为证明我们的主要结果,需要如下的加权Bochner公式[2-4]. 引理1 对任意的光滑函数u,有 引理2 对任意的θ>0,δ>0,有 (2.1) 对任意的A>0,B>0,0 (A+B)v≤Av+Bv. (2.2) 证明 先证(2.1). 所以f(a)≥0. 再证(2.2). 所以,f(A)单调递增,从而有f(A)>f(0),即(A+B)v≤Av+Bv. 令lnu=w,即u=ew,则 ∂tu=ew∂tw=u∂tw, ▽u=ew▽w=u▽w, Δu=div(▽u)=div(u▽w)=▽u·▽w+udiv(▽w)=▽u·▽w+uΔw=u|▽w|2+uΔw. 由于u>0为(1.2)的正解,于是u∂tw-(Δu-▽u·▽f)=A,则 u∂tw-(u|▽w|2+uΔw)+u▽w·▽f=A. u∂tw-u(Δw-▽w·▽f)-u|▽w|2=A. u∂tw-uΔfw-u|▽w|2=A. 因此, ∂tw-Δfw-|▽w|2=u-1A. (3.1) 容易得到 ▽F=▽|▽w|2(1-w)-2+|▽w|2▽(1-w)-2. 以及∂tF=2▽w·▽(∂tw)(1-w)-2+|▽w|2(-2)(1-w)-3(-∂tw). ∂tF=2▽w·▽(Δfw+|▽w|2+u-1A)(1-w)-2+2|▽w|2(1-w)-3(Δfw+|▽w|2+u-1A). (3.2) 作如下计算 ΔfF=ΔF-▽F·▽f=div(▽F)-▽F·▽f=div[(1-w)-2▽|▽w|2+|▽w|2▽(1-w)-2]-(1-w)-2▽|▽w|2·▽f-|▽w|2▽(1-w)-2·▽f=(1-w)-2·Δ|▽w|2+2▽|▽w|2·▽(1-w)-2+|▽w|2Δ(1-w)-2-(1-w)-2▽|▽w|2·▽f-|▽w|2▽(1-w)-2·▽f =(1-w)-2Δf|▽w|2+|▽w|2Δf(1-w)-2+2▽|▽w|2·▽(1-w)-2. 由(1.4)以及加权Bochner公式,可以得到 (∂t-Δf)F=⎣2▽w·▽Δfw+2▽w·▽|▽w|2+2▽w·▽(u-1A)」·(1-w)-2+2|▽w|2(1-w)-3(Δfw+|▽w|2+u-1A) -(1-w)-2[2|Hessw|2+2▽w·▽Δfw+2Ricf(▽w,▽w)] -|▽w|2Δf(1-w)-2-2▽|▽w|2·▽(1-w)-2. (3.3) 由于 ▽(1-w)-2=-2(1-w)-3(-▽w)=2(1-w)-3▽w. Δf(1-w)-2=Δ(1-w)-2-▽(1-w)-2·▽f=div(2(1-w)-3▽w)-2(1-w)-3▽w·▽f=2(1-w)-3▽fw+6(1-w)-4|▽w|2. 将以上两式代入(3.3),得到 (∂t-Δf)F=⎣2▽w·▽|▽w|2+2▽w·▽(u-1A)」·(1-w)2+2|▽w|2(1-w)-3(Δfw+|▽w|2+u-1A) -(1-w)-2[2Ricf(▽w·▽w)] -2(1-w)-3|▽w|2Δfw-6|▽w|4(1-w)-4-4(1-w)-3▽|▽w|2·▽w. 由(1.3)得Ricf(▽w,▽w)≥-K2|▽w|2,所以 (∂t-Δf)F≤[2▽w·▽|▽w|2+2▽w·▽(u-1A)](1-w)-2+2|▽w|2(1-w)-3(|▽w|2+u-1A) +2K2(1-w)-2|▽w|2-4(1-w)-3▽|▽w|2·▽w-6(1-w)-4|▽w|4. 显然 ▽(u-1A)=-u-2A▽u+u-1▽A=-u-2(u▽w)A+u-1▽A=-u-1A▽w+u-1▽A. 于是 (∂t-Δf)F≤-2▽w·▽|▽w|2(1-w)-3(1+w)+2u-1(1-w)-2(-A|▽w|2+▽w·▽A) -2|▽w|4(1-w)-4(2+w)+2K2(1-w)-2|▽w|2+2|▽w|2(1-w)-3u-1A. (∂t-Δf)F≤-2(1-w)-3(1+w)▽w·▽[F(1-w)2]+2u-1(1-w)-2(-AF(1-w)2+▽w·▽A) -2F2(1-w)4(1-w)-4(2+w)+2K2(1-w)-2F(1-w)2+2(1-w)-3u-1AF(1-w)2. 而 ▽[F(1-w)2]=(1-w)2▽F+F▽(1-w)2=(1-w)2▽F+F·2(1-w)(-1)▽w=(1-w)2▽F-2(1-w)F▽w. 所以 (∂t-▽f)F≤-2(1-w)-2(1+w)▽w·[(1-w)▽F-F·2▽w] +2u-1(1-w)-2[-AF(1-w)2+▽w·▽A] -2F2(2+w)+2K2F+2(1-w)-1u-1AF. 整理得到 (∂t-Δf)F≤[2-4(1-w)-1]▽w·▽F+2wF2+2Fu-1Aw(1-w)-1+2u-1▽w·▽A(1-w)-2+2K2F. (3.4) 则 (∂t-Δf)(tF)=F+t(∂t-Δf)F. (3.5) 令G(x,t)=tF(x,t).由于M紧致无边,则G(x,t)在M×[0,T]有最大值,不妨记之为G(x0,t0).若G(x0,t0)≤0,则定理成立,因为对任意的(x,t)∈M×[0,T],G(x,t)≤G(x0,t0)≤0,即F≤0.若G(x0,t0)>0,则t0>0,此时, ▽G(x0,t0)=0. (3.6) 因为,ΔfG=ΔG-▽G·▽f,所以, ΔfG(x0,t0)≤0. (3.7) 下面说明 ∂tG(x0,y0)≥0. (3.8) 由(3.7)和(3.8)得 (∂t-Δf)G(x0,t0)≥0. (3.9) 由(3.6)有▽F(x0,t0)=0.由(3.5)和(3.9)在(x0,t0)处有 0≤F+t(∂t-Δf)F≤F+t[2wF2+2Fu-1Aw(1-w)-1+2u-1▽w·▽A(1-w)-2+2K2F]. 即0≤F+2wtF2+2tFw(1-w)-1u-1A+2tu-1▽w·▽A(1-w)-2+2tK2|▽w|2(1-w)-2. 结合条件(1.5),因为u-1A≤Q,▽w·▽A≤|▽w|·|▽A|,所以在(x0,t0)处有 0≤F+2wtF2+2tFw(1-w)-1Q+2tu-1|▽w||▽A|(1-w)-2+2tK2F. 从而 上式两边同时乘以t,得到 由于tF=G,所以上式可变形为 (3.10) 或者 (3.11) 上式左右两边同时乘以1+2tQ+2tK2,有 代入(3.11)中,得到 于是 对任意的(x,t)∈M×[0,T],G(x,t)≤G(x0,t0),则 由于T>0,因此(1.6)成立. [1]P.Li,S.T.Yau.On the parabolic kernel of the Schrodinger operator[J].Acta Mathematica,1986(156):153-201. [2]X.D.Li,Liouville theorems for symmetric diffusion operators on complete Riemannian manifolds[J].Journal de Mathematiques Pureset Appliques,2005,84(10):1295-1361. [3]J.Lott.Some geometric properties of the Bakry-Emery Ricci tensor[J].Commentarii Mathematici Helvetici, 2003(78):865-883. Elliptic Type Gradient Estimate for Non-homogeneous Heat Equation on Compact Manifolds XIE Fei (Nantong Normal College, Rugao Jiangsu 226500, China) In this paper,by using the weighted Bochner formula and the maximum principle,we discuss the elliptic type gradient estimate for positive solutions to the following non-homogeneous weighted linear heat equation (∂t-Δf)u=A(x,t) on compact manifolds, whereA(x,t) is a smooth function defined onM×[0,+∞). compact manifolds; elliptic type gradient estimate 2015-07-11 谢 飞(1982- ),女,江苏如皋人,南通师范高等专科学校讲师,从事数学教育研究。 O186 A 2095-7602(2015)10-0005-05
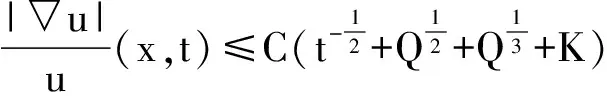
2 引理
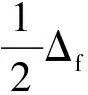



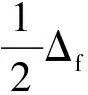


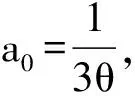

3 主要结果