Precipitation Changes in Wetand Dry Seasons over the 20th Century Simulated by Two Versions of the FGOALS M odel
MA Shuangmeiand ZHOU Tianjun
1State Key Laboratory of NumericalModeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing100029
2University of Chinese Academy of Sciences,Beijing100049
3Climate Change Research Center,Chinese Academy of Sciences,Beijing100029
Precipitation Changes in Wetand Dry Seasons over the 20th Century Simulated by Two Versions of the FGOALS M odel
MA Shuangmei1,2and ZHOU Tianjun∗1,3
1State Key Laboratory of NumericalModeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing100029
2University of Chinese Academy of Sciences,Beijing100049
3Climate Change Research Center,Chinese Academy of Sciences,Beijing100029
Seasonal precipitation changes over the globe during the 20th century simulated by two versions of the Flexible Global Ocean–Atmosphere–Land System(FGOALS)model are assessed.The two model versions differ in terms of their AGCM component,but the remaining parts of the system are almost identical.Both models reasonably reproduce the mean-state features of the timings of the wetand dry seasons and related precipitation amounts,w ith pattern correlation coefficients of 0.65–0.84 w ith observations.Globally averaged seasonalprecipitation changes are analyzed.The results show thatwetseasons getwetterand the annual range(precipitation difference between wetand dry seasons)increases during the 20th century in the two models,w ith positive trends covering most parts of the globe,which is consistentw ith observations.However, both models show a moistening dry season,which is opposite to observations.Analysis of the globally averaged moisture budget in the historical climate simulations of the two models shows little change in the horizontal moisture advection in both the wetand dry seasons.The globally averaged seasonal precipitation changes are mainly dominated by the changes in evaporation and vertical moisture advection.Evaporation and vertical moisture advection combine to make wet seasons wetter and enhance the annual range.In the dry season,the opposite change of evaporation and verticalmoisture advection leads to an insignificant change in precipitation.Verticalmoisture advection is the most important term thatdetermines the changes in precipitation,wherein the thermodynam ic component is dom inantand the dynam ic component tends to offset the effectof the thermodynam ic component.
20th century historical climate simulation,FGOALS-g2,FGOALS-s2,wet season,dry season,precipitation change,water vaporbudgetdiagnosis
1.Introduction
Precipitation is not only a natural feature of Earth’s weather systems,but also has an irreplaceable role in the global hydrological cycle.As the rainfall amount,intensity and frequency vary spatially and temporally,rainfall plays a key role in forming the climate of certain areas.However,some changes in precipitation,e.g.the intensity and frequency increases thathave led to severe droughtand flooding during the last three decades(A llan and Soden,2008),may exertadverse effects on agriculture,water resources,human health and infrastructure.Understanding the main characteristics of and reasons for precipitation changes has therefore become a major focus of the climate change research community and is of greatconcern to society.
Great efforts have been devoted to understanding how the global hydrological cycle,in particular global precipitation,responds to a warm ing climate(Held and Soden, 2006;Vecchi and Soden,2007;Wentz et al.,2007;Zhang et al.,2007;Trenberth,2011;William et al.,2013).Under globalwarm ing,the global-mean precipitation simulated by global coupled atmosphere–ocean general circulation models(AOGCM s)tends to increase ata rate of about1%to 3% K-1(Held and Soden,2006;Vecchi and Soden,2007;Andrews et al.,2010).In a warming climate,coupled climate models projectglobally more heavy precipitation,less moderate precipitation,and more light precipitation(Allan and Soden,2008;A llan et al.,2010;W illiam et al.,2013).In addition to an increase in global-mean precipitation,coupled AOGCM s suggest that global warm ing causes a latitudinal redistribution of precipitation,w ith increasing precipitation athigh and deep tropical latitudes,and decreasing precipitation atsubtropical latitudes(Held and Soden,2006;Zhang etal.,2007;Scheffand Frierson,2012;Noake etal.,2012;Polson etal.,2013).The above-mentioned precipitation changes are evidentin observations,butthe amplitudes of the changes simulated by coupled climate models are generally smaller than observed(Zhang etal.,2007;A llan etal.,2010;Zhou et al.,2011;Noake etal.,2012).
The main contribution of global-mean precipitation comes from tropical convective precipitation.The pattern of tropical precipitation change is dom inated by two mechanisms:“wet-get-wetter”(Chou and Neelin,2004)and“warmer-get-wetter”(Xie et al.,2010).The wet-get-wetter mechanism argues that precipitation increases in the core of major tropical rainbands(Allan et al.,2010;Zhou et al., 2011).This pattern is generally explained by the increase of atmospheric moisture in a warmer climate.If one ignores changes in atmospheric circulation,the moisture flux convergence in regions w ith climatological convergence tends to increase as moisture increases and then enhances the corresponding precipitation(Chou and Neelin,2004;Held and Soden,2006;Chou etal.,2009).The warmer-get-wetter pattern involves precipitation increases in places where the rise in sea surface temperature(SST)exceeds the mean surface warming of the tropics(Xie et al.,2010;Chadw ick et al., 2013).A recent study showed that both the wet-get-wetter and warmer-get-wetter mechanisms are important for tropical precipitation change,dom inating the annual mean and seasonalanomalies,respectively(Huang etal.,2013).
Precipitation change has a strong seasonal dependence because of the strong seasonal cycle of atmospheric circulation(Seager et al.,2010;Noake et al.,2012;Polson et al.,2013).Coupled climate model simulations show that the globally averaged annual range(AR)of precipitation tends to increase under global warming,and the increase largely comes from moistening of the wet season(Chou and Lan, 2012).Such changes have been detected in observations,especially over the past few decades(Chou etal.,2013).However,studies on the seasonalprecipitation change in a warming climate remain quite limited.
Climate system models(CSMs)play an instrumental role in understanding and simulating past,present and future climates.The State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics,Institute of Atmospheric Physics,Chinese Academy of Sciences(LASG/IAP/CAS)has devoted great efforts to the development of component models and fully coupled models(see Zhou et al.,2007,2014).New versions of the Flexible GlobalOcean–Atmosphere–Land System model (FGOALS)have been established and are participating in the ongoing Coupled Model Intercomparison Project Phase 5(CM IP5)experiments.Two versions of the FGOALS model,FGOALS-g2 and FGOALS-s2,share the same coupling framework,ocean and land components,butadoptdifferentatmospheric and sea ice components(Bao etal.,2013; Li et al.,2013).Confidence in model projection is closely related to the ability to simulate the recent climate and climate changes w ith sufficient realism.The performances of the FGOALS models in simulating major climate phenomena,e.g.annual SST cycles and the 20th century globaland regional surface air temperature changes,ENSO–monsoon relationship,and globalmonsoons,have been assessed(Liet al.,2013;Bao etal.,2013;Wu and Zhou,2013;Zhou etal., 2013a;Zhang and Zhou,2014).However,the performance of FGOALS in the simulation of seasonalprecipitation changes in wet and dry seasons during the past century have never been assessed.
The current study aims to evaluate the performance of the LASG/IAP model in the simulation of seasonal precipitation.The follow ing questions are addressed:(1)How well do the two versions of FGOALS simulate the mean state of the timing of the wetand dry seasons and related precipitation amounts?(2)What are the characteristics of precipitation change in the wet and dry seasons,especially the AR, during the 20th century in the historical climate simulations performed by the FGOALS models?(3)Whatare the mechanisms responsible forprecipitation change in the wetand dry seasons?Since the long-term change of global precipitation in 20th century historical climate simulations is dom inated by the responses of the coupled system to greenhouse gas forcing,and many ocean–atmosphere feedback processes are involved,only fully coupled climate models can be used in this kind of diagnosis(Xie etal.,2010;Chou and Lan,2012; Chadw ick etal.,2013).
2.M odel,data and analysis method
2.1.Model,experiments and data description
Both FGOALS-g2 and FGOALS-s2 are composed of four interactive component models,including atmospheric, oceanic,land and sea ice models thatare coupled togetherby the NationalCenter for Atmospheric Research’s flux coupler module,version 6(CPL6).These two versions of FGOALS share the same ocean and land component models,but differ in their atmospheric and sea ice components.The ocean componentof FGOALS is the LASG/IAP’s Climate System Ocean Model version 2(LICOM 2),which has a horizontal resolution of about 1◦×1◦in the extratropical zone and 0.5◦×0.5◦in the tropics,and 30 vertical levels.The land componentis the Community Land Modelversion 3(CLM 3). For FGOALS-s2,the atmospheric component is the Spectral Atmospheric Modelof the IAP/LASG version 2(SAM IL2), w ith a horizontal resolution ofabout2.81◦(lon)×1.66◦(lat) and 26 levels in the vertical direction;the sea ice component is the Community Sea Ice Modelversion 5(CSIM 5)(Bao et al.,2013).In FGOALS-g2,the atmospheric componentis the Grid-point Atmospheric Model of the IAP/LASG version 2 (GAM IL2),w ith a horizontal resolution ofabout2.8◦×2.8◦and 26 levels in the vertical direction;the sea ice component is the Los A lamos Sea Ice Model(CICE)(Li et al.,2013). For more detailed information about these two model versions,readers are referred to Bao et al.(2013)and Li et al. (2013).
In this study,the outputs of the 20th century historical climate simulationsand pre-industrialcontrolsimulations(PIcontrol)by the two versions of FGOALS are diagnosed.The 20th century historical climate simulation is a standard experiment of CM IP in which the models are forced by various and identical historical atmospheric forcing agents recommended by CM IP(Zhou and Yu,2006).The PI control run integrated starting from the equilibrium state of a standalone 500-yr spin-up integration of LICOM 2.The values of external forcing agents in the PI control run were fixed at the level of the year 1850(Bao et al.,2013;Liet al.,2013). More details of the experimentdesign can be found Taylor et al.(2012).In addition,the monthly mean precipitation from the Global Precipitation Climatology Project(GPCP)(Adler et al.,2003)is used as the observational evidence to gauge the modelperformance.
2.2.Analysis method
The wet season,also called the rainy season,is an annually recurring period of one ormore months during which precipitation is at a maximum for that region;the opposite is the dry season.In previous studies,the AR of precipitation has been defined as the local summer-m inus-w inter precipitation,w ith summermeaning June–July–August(JJA) in the Northern Hem isphere(NH)and December–January–February(DJF)in the Southern Hem isphere(SH)(Wang and Ding,2006;Zhou et al.,2008).So,the NH(SH)share the same and fixed occurrence times of the wet(dry)season everywhere.
In fact,the timingsof the wetand dry seasonsare strongly dependenton geographic location.In addition,the wetand dry seasons could shift under global warm ing.Trenberth et al.(2003)suggested that the liquid-precipitation season has become longer by up to 3 weeks in some regions of the borealhigh latitudes over the last50 years,ow ing to an earlier onsetof spring.Over the United States,from 1930 to 2009, the day of the year on which certain percentiles of annual totalprecipitation were achieved indicated spatially coherent patterns of change;regionally consistent trends in the tim ing of wet(dry)seasons were also evident,particularly over the Ohio(M issouri)River valleys where the dry season arrived up to 2–3 weeks earlier(later)(Pryorand Schoof,2008).The same phenomena have been found in other studies(Paletal., 2013).So,fixed wet and dry seasons do not necessarily delineate the timing of wet and dry season precipitation at a particularstation and the changes therein.
Recognizing the changing behavior of the tim ing of wet and dry seasons,in our study we define the AR as the precipitation difference between the wet and the dry season in each year and at each grid or station,follow ing Chou etal. (2013).The wet(dry)season is defined as an annually recurring period of 3 months during which precipitation is maximum(m inimum)for that grid,and the central point of the 3 months is used to denote the tim ing of the wetor dry season. So,the tim ing of the wet(dry)season varies temporally and spatially.
In the analysis,we fi rst convert the monthly products of the observed and simulated fi elds to seasonal variables,using 3-month running averages.Then,the maximum values of seasonal precipitation for each grid and each year are calculated and referred to as the wet-season precipitation amount of thatgrid and thatyear.The time when the maximum seasonal precipitation occurs for each grid and each year is the occurrence time of the wetseason for thatgrid and thatyear. Corresponding strictly to the wet season of each grid and each year,values of related climate variables,e.g.evaporation,vector w inds and specific hum idity,of thatgrid and that year are extracted.The above wet-season data processing is also applied to the dry season,which is based on the m inimum values of seasonal precipitation.The area-weighted averages are calculated for the global regions.Resultant globally averaged wet(dry)season precipitation means the globalprobable maximum(m inimum)seasonalprecipitation amount.The resultant wet(dry)season evaporation is the evaporation amount when precipitation reaches its seasonal maximum(minimum).As the wetand dry season varies from grid to grid and year to year,the resultantglobally averaged convergence ofmoisture flux cannotbe zero.Thus,the global mean wet(dry)season precipitation cannot be balanced by the globalmean wet(dry)season evaporation.Here,the climatology is calculated for the period 1979–2005.
In order to understand the mechanisms responsible for precipitation changes in the wet and dry season and the AR, as in previous studies(Held and Soden,2006;Seager et al., 2010;Chou and Lan,2012;Huang et al.,2013)we start from the vertically integrated moisture equation,which can be w ritten as
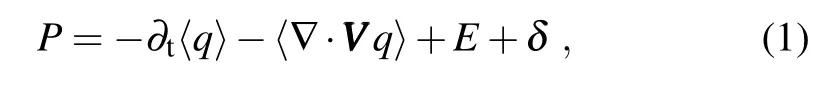
wherePis precipitation,Eis evaporation andVVVis vector w ind.The symbol〈〉means a mass integration through the entire troposphere.A ll values in Eq.(1)are seasonally averaged.∂t〈q〉is the time derivative of specific hum idityqand can generally be ignored as its seasonalmean value is much smaller than thatofother terms.-〈∇·VVV q〉is the convergence of moisture flux.δis a residual term,which includes transienteddies(water vapor transportat the sub-seasonal time scale)and contributions from surface processes due to topography(Seager et al.,2010).Based on the mass conservation equation,i.e.∇·VVV=0 and follow ing Chou et al.(2009, 2013)and Chou and Lan(2012),the convergence of moisture flux-〈∇·VVV q〉can be divided into two terms:vertical moisture advection-〈ω∂pq〉and horizontal moisture advection-〈VVVh·∇hq〉.∇his the horizontal differential operator. Equation(1)can then be approximately w ritten as

where the subscripts“p”and“h”denote pressure and horizontaldirection,respectively.ωis pressure velocity andVVVhis horizontalvectorw ind.Verticalmoisture advection-〈ω∂pq〉is the partof the convergence ofmoisture flux induced by verticalmotion.If the pressure velocityωis assumed to be zero at the surface and at the tropopause,we get〈∂pωq〉=0 and -〈ω∂pq〉=-〈q∇h·VVVh〉.So,the verticalmoisture advection is also referred to as the horizontal flow convergence of themoisture term(Seager et al.,2010).Note that the vertical moisture advection is associated w ith the low-level convergence;the low-level convergence can promote the upward transport of moisture and then can greatly speed up the rain formation.
According to Eq.(2),we can decompose the precipitation changes into

Here,primes indicate departures from the climatology.As any dependent variable can be divided into a constant basic state portion(denoted by an overbar)and a perturbation portion(denoted by a prime),so the pressure velocity ωand the specific hum idityqcan be described as follows:Changes of the vertical moisture advectioncan be furtherapproximated as
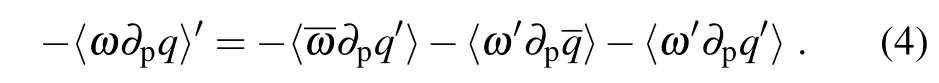
The atmospheric boundary layercontains the bulk of columnintegrated atmospheric water.Boundary layerspecific hum idity is constrained by the surface energy balance to increase w ith temperature approximately follow ing the Clausius–Clapeyron relation(Boer,1993;Held and Soden,2000).The fi rst term on the right of Eq.(4)only involves changes in specific hum idityqbut no changes in pressure velocityω; the second term only involves changes in pressure velocity ωbut no changes in specific hum idityq.In other words,is associated w ith changes in water vapor,which is mainly induced by temperature changes;〉is associated w ith changes in pressure velocity,which is mainly induced by atmospheric circulation changes.Follow ing previous studies(Chou and Lan,2012;Chou etal.,2013;Huang et al.,2013),〉is termed the thermodynamic component andis termed the dynam ic component ofThe last term on the rightof Eq.(4)is the nonlinear term that is the productof changes both in vertical pressure velocityωand water vaporq.As the contribution of horizontalmoisture advection to precipitation changes is relatively small,it is notdivided into the thermodynamic component and dynam ic component as is the case for vertical moisture advection.So,as in previous studies(Chou et al., 2009;Chou and Lan,2012;Chou et al.,2013;Huang et al., 2013),in this study the thermodynam ic and dynam ic component refers specifically torespectively.Unlike in Seager et al.(2010),thermodynam ic contributors refer to all changes in specific humidityqbut no changes in w indVVVon the rightside of Eq.(3),and dynam ic contributors refer to all changes inVVVbutno changes inq.
3.Results
In the follow ing analysis we fi rst examine the performance of the two versions of FGOALS in reproducing the spatialdistribution of the tim ing of the climatologicalwetand dry seasons.We also exam ine the climatology of the precipitation of the wet and dry seasons,and the AR,in models by comparing their results w ith observations.We then evaluate the precipitation change in the wet and dry seasons of the 20th century historical climate simulations.The changes in AR are also analyzed.Finally,the possible mechanisms responsible for the changes of seasonalprecipitation are discussed.
3.1.Climatologicalmean state
The climatological wet(dry)season is defined as three consecutive months during which precipitation reaches its maximum(minimum)based on the climatological12-month mean precipitation.The climatological spatial distributions of the tim ings of the wetand dry seasons,which are derived from observations and the simulations of FGOALS-g2 and FGOALS-s2,are shown in Fig.1.The observations are dominated by two features.First,generally,the wet season is mainly in the summer–autumn months,while the dry season is mainly in the w inter–spring months(Figs.1a and b). Second,substantial spatial features are evident in the occurrence of the climatological wet and dry seasons.In northwestern Europe,most of Asia,small areas of northwestern North America,the South China Sea,southern Africa,northern Australia,parts of the southern tropical Pacific,and Central America,the wet season mainly occurs in summer and the dry season mainly in w inter.Autumn is the tim ing of the wet season in most parts of the tropical Atlantic.The wet season occurs in July–August–September(JAS)(one month later than boreal summer)in the Arctic Ocean.The wetand dry seasons over the subtropical oceans tend to start from the w inter and summer months,respectively.Autumn corresponds to the wetseason in the Southern Ocean.
The timings of the climatologicalwetand dry seasons in the two models show spatialpatterns thatare similar to those in the observations(Figs.1c–f),but some biases are also evident.The largest deficiency is a delayed occurrence of the wet and dry seasons in most global regions in the two models(Fig.2).However,regional details are different.In FGOALS-g2,the startof the wetordry season is earlier than in the observation in most of the high latitudes,but later in most of the m iddle and low latitudes(Figs.2a and c).In FGOALS-s2,over the Arctic,northern Europe,extensions of the western boundary currents,the equatorial Pacific,and the Gulf of Mexico,both the wetand dry seasons start later than in the observations.In northern Asia,the wet season starts later but the dry season starts earlier than in observations(Figs.2b and d).
To quantitatively evaluate the models’performances in their simulations of the timing of the climatological wet and dry seasons,the weighted pattern correlation coefficient (PCC),root-mean-square difference(RMSD)and standard deviation ratio(SDR)of the occurrence time of the climatologicalwetand dry seasons between the models and observation are calculated.For the wet season,FGOALS-g2 and FGOALS-s2 both show a PCC of 0.65,which is statistically significant at the 1%level.The standard deviations of the simulations in both models are larger than that in the observation,and SDRs are also the same at 1.05.The RMSD is2.11 in FGOALS-g2 and 2.31 in FGOALS-s2.The abilities of FGOALS-g2 and FGOALS-s2 in reproducing the mean occurrence of the wet season are equivalent.For the dry season,compared to FGOALS-s2,FGOALS-g2 has a larger PCC and SDR:the PCC is 0.66 in FGOALS-g2 and 0.63 in FGOALS-s2,both ofwhich are statistically significantat the 1%level;the SDR(RMSD)is 1.12(2.24)in FGOALS-g2 and 1.03(2.38)in FGOALS-s2.Therefore,on the whole, both FGOALS-g2 and FGOALS-s2 can reasonably simulate the mean tim ings of the wetand dry seasons.

Fig.1.Tim ing of the(a,c,e)climatologicalwetseason and(b,d,f)dry season from(a,b)observations,(c,d) FGOALS-g2 and(e,f)FGOALS-s2.The numbers 1 to 12 in the color bar indicate the time that the wetand dry seasons occur,1:DJF(Dec–Feb);2:JFM(Jan–Mar);3:FMA(Feb–Apr);4:MAM(Mar–May);5:AMJ (Apr–Jun);6:MJJ(May–Jul);7:JJA(Jun–Aug);8:JAS(Jul–Sep);9:ASO(Aug–Oct);10:SON(Sep–Nov); 11:OND(Oct–Dec);12:NDJ(Nov–Jan).
Buthow well do the two versions of FGOALS simulate the climatology of seasonal precipitation?Figure 3 shows the spatialdistributions of climatological precipitation in the wet and dry seasons.For the wet season,observed values of precipitation vary spatially from less than 0.2 mm d-1or to a maximum of more than 14 mm d-1(Fig.3a).The distribution of precipitation is sim ilar to the annualmean precipitation(figure not shown).Precipitation is dom inated by atmospheric circulation,surface temperature and watervapor conditions.Therefore,the distribution of precipitation in the wetseason has features as follows.Deserts are evident in the subtropical regions.Dry regions are seen in continental areas and polar areas.The areas near the equator receive high amounts of precipitation.Precipitation has a secondary maximum over the North Pacific and Atlantic oceans.
The climatological wet season precipitation in the two models has a spatial pattern sim ilar to that of GPCP,w ith a PCC of 0.84(0.83),RMSD of 2.03(2.10),and SDR of 1.10 (1.11)for FGOALS-g2(FGOALS-s2).However,biases are still evident.In the tropical regions,stronger precipitation over the western Indian and centralPacific near the equator is evidentin the two modelversions(Figs.3c and e).There are clear double Intertropical Convergence Zone(ITCZ)structures about the simulated climatological wet season precipitation in the two versions of the FGOALS model.Precipitation overSouth America and northeastern Europe is underestimated in both models.
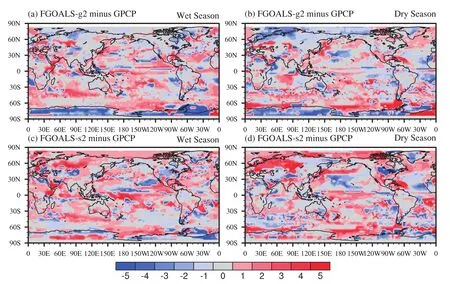
Fig.2.The difference in the tim ing of the climatologicalwetand dry seasons between the models and observations:(a,b)FGOALS-g2 m inus GPCP;(c,d)FGOALS-s2 m inus GPCP;(a,c)wetseason;(b,d)dry season. Units:months.

Fig.3.Climatological precipitation of the(a,c,e)wetseason and(b,d,f)dry season based on(a,b)observations,(c,d)FGOALS-g2 and(e,f)FGOALS-s2.Units:mm d-1.
In the dry season,except for specific regions such as the ITCZ,South Pacifi c Convergence Zone(SPCZ),equatorial Indian and Amazon,precipitation is weak over the entireglobe(Figs.3b,d and f).The PCC between the simulation and observation is 0.84(0.83)for FGOALS-g2(FGOALS-s2).The corresponding SDR is 0.96(1.08)and RMSD is 2.03 (2.11)for FGOALS-g2(FGOALS-s2).Both models overestimate the precipitation over the ITCZ and SPCZ w ith a double ITCZ structure,butunderestimate the precipitation over the midlatitude Atlantic and the northern Pacific.
The observed and simulated spatial distributions of the climatological AR of precipitation are shown in Fig.4.The maximum centers of AR are mainly located in or near the boundary between the sea and land.Over the equatorial Atlantic,Amazon and equatorial Africa,the maximums of AR are evident.The PCC,RMSD and SDR is 0.81,1.78 and 1.11(0.80,1.79 and 1.09)for FGOALS-g2(FGOALS-s2), respectively.A larger AR over the central equatorial Pacific and Indian oceans is simulated in the two models.
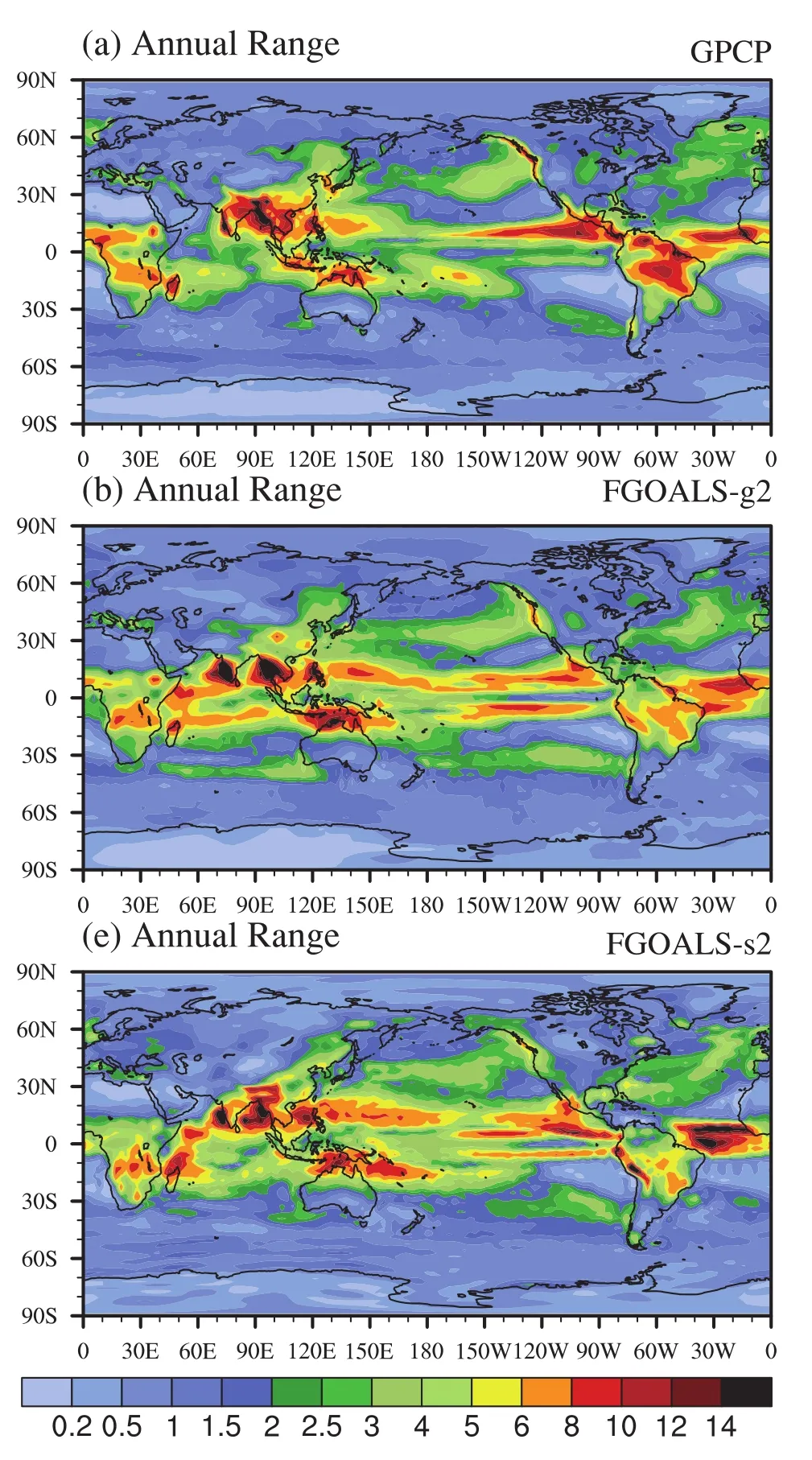
Fig.4.As in Fig.3 except for the annual range of precipitation.
There are clear double ITCZ structures in the two coupled versions of FGOALS.However,the contribution of the spurious ITCZ in the SH to globally averaged precipitation is limited.Previous studies have demonstrated that if coupled climate models demonstrate reasonable performance in reproducing the mean state of global precipitation,the double ITCZ problem cannot prevent us from exam ining global precipitation change and discussing related dynam icalcauses through using these models,and thus they have been w idely used in studies ofglobalprecipitation changes(Held and Soden,2006;Seager et al.,2010;Chou and Lan,2012;Huang et al.,2013).Chapter 9 of theIntergovernmental Panel on Climate Change Fifth Assessment Report(IPCC AR5)states that the mean state biases do not obviously affect the modeled response to greenhouse gas forcing(Flato etal.,2013). The above assessment indicates reasonable performance of the two versions of FGOALS in reproducing the tim ing of climatological wet and dry seasons and related precipitation amounts.This forms a solid base for our analysis in the follow ing two sections of the seasonal precipitation response to globalwarm ing in the 20th century assimulated by FGOALS.
3.2.Precipitation changes in the 20th century
To assess the impactofglobalwarming on the hydrologicalcycle,records longer than 100 years are required(Vecchi et al.,2006).For periods shorter than 100 years,it is very likely thatthe multi-decadalinternalvariability dom inates the long-term trend.However,observational data on global precipitation are only available from 1979(Adler etal.,2003), and the 20th century historical simulations of FGOALS-g2 and FGOALS-s2 only cover 1850–2005.Therefore,simulated temporalevolutions of globalmean precipitation in the wetand dry seasons,and the AR,during 1850–2005 are plotted against the observationsduring 1979–2012 in Fig.5.The observation and model results are both normalized by their climatologicalmean.In the observations,the mean value of globally averaged precipitation for the wet season is 4.5488 mm d-1.For the dry season the value is 1.2407 mm d-1, and the AR is 3.3080 mm d-1.In FGOALS-g2(FGOALS-s2),the mean value ofglobally averaged precipitation for the wetseason,dry season and AR is 4.9058,1.2840 and 3.6219 (4.8711,1.1203 and 3.7508)mm d-1,respectively.For the wet season,the globally averaged precipitation in both observation and model results show significant upward trends, w ith rates of 0.2576 mm d-1(34 yr)-1,0.0491 and 0.2051 mm d-1(156 yr)-1for GPCP,FGOALS-g2 and FGOALS-s2,respectively.All these trends exceed the 99%confidence levelof the Student’st-test.Note that PIcontrol simulations can be used as an indicator of natural variability w ithoutanthropogenic impacts.Based on the PI control simulations of both models,we estimate that the w idth of the 95%confidence interval of the 156-year trend is±0.0245(0.0351) mm d-1(156 yr)-1for FGOALS-g2(FGOALS-s2).Therefore,this upward trend of maximum precipitation is mainly the model response to external forcing rather than internal variability.

Fig.5.Time series of globally averaged precipitation during the 20th century, normalized to units by the mean over 1979–2005:(a)wetseason;(b)dry season;(c)annual range.Black lines correspond to the observational records of the GPCP over 1979–2012;red and blue lines correspond to the 20th century historicalsimulations for the period 1850–2005 of FGOALS-g2 and FGOALS-s2, respectively.
For the dry season,observations show a drying trend over the last three decades w ith a rate of-0.1699 mm d-1(34 yr)-1,which is statistically significantat the 1%level.Chou etal.(2013)found that the sign of precipitation tendency for the dry season is inconsistent among different observational data.Hence,caution should be applied to this observed drying trend.The trend of globally averaged precipitation in the dry season is positive in both models,w ith a rate of 0.0017 (0.0115)mm d-1(156 yr)-1for FGOALS-g2(FGOALS-s2), butboth are statistically insignificantat the 5%level.
It is evident that the magnitude of precipitation change in the wetseason is stronger than that in the dry season in both observations and the modelsimulations.As a result,the AR of precipitation increases significantly.Importantly,the observed wetterwetseason and drierdry season combine to enhance the AR.However,in both FGOALS-g2 and FGOALS-s2,the simulated moistening of the dry season offsets the contribution of the wetter wet season in terms of the simulated increase of the AR.The observed increasing trend of the AR over 1979–2012 is 0.4275 mm d-1(34 yr)-1.The simulated increasing trend of the AR over 1850–2005 is 0.0474 (0.1936)mm d-1(156 yr)-1for FGOALS-g2(FGOALS-s2). A llof these three trends are statistically significantat the 1% level.
The signs of the globally averaged precipitation trend for the wetseason and the AR are consistentbetween the observations and simulations.However,the trends derived from the observations are larger than those derived from the simulations.This phenomenon is also evident in other models (A llan et al.,2010;Chou et al.,2013;Polson et al.,2013). Nevertheless,the reasons responsible for the discrepancy remain unknown.One possible explanation is that the time span of three decades for the observational record is too short to distinguish the effectofGHG-forced globalwarm ing from natural variability.For detection periods shorter than 100 years,it is very likely that the decadal internal variability, such as mega ENSO,Pacific Decadal Oscillation(PDO)or Interdecadal Pacific Oscillation(IPO)events,dominates the long-term changes of the coupled climate system(Vecchiet al.,2006).In fact,recent studies have demonstrated that mega-ENSO(a leading mode of interannual-to-interdecadal variation of globalSST)and the Atlantic MultidecadalOscillation have intensified the globalmonsoon precipitation during the most recent three decades(Wang etal.,2012,2013). The changes of the East Asian summer monsoon(EASM) precipitation are largely dom inated by natural internal variability of the PDO,resulting in the EASM exhibiting no significant long-term trend during the 20th century(Zhou etal., 2009;Li et al.,2010;Zhou et al.,2013b;Qian and Zhou, 2014).As the phase of the multi-decadal mode in coupled models is not in sync w ith those in observations,and the natural decadal variability in the two versions of FGOALS during the 20th century may be weaker than thatin observations,the observed trend magnitude is larger than those simulated by FGOALS-g2 and FGOALS-s2.Another possible explanation is that there are errors in observational records,which may lead to a spuriously large observed trend(A llan et al., 2010).
Regardless of whether for the wet season,dry season, or AR,the linear trend of the globally averaged precipitation in FGOALS-g2 during 1850–2005 is smaller than that simulated by FGOALS-s2.This discrepancy may be related to the model’s sensitivity to the external radiative forcing.FGOALS-s2 has a larger climate sensitivity(4.5 K), defined as the equilibrium temperature change under double CO2forcing,than FGOALS-g2(3.7 K)(Chen et al., 2014).Zhou et al.(2013a)exam ined the historical evolution ofglobalsurface air temperature simulated by FGOALS-g2 and FGOALS-s2 during 1850–2005 and suggested that FGOALS-s2 has a stronger response to anthropogenic forcing,because the sea-ice albedo feedback and water vapor feedback in FGOALS-s2 is stronger than those in FGOALS-g2.

Fig.6.The observed(1979–2012)and simulated(1850–2005)changes in precipitation amount calculated from linear regression:(a,b)GPCP;(c,d)FGOALS-g2;(e,f)FGOALS-s2;(a,c,e)wet season;(b,d, f)dry season.The interval of each percentile bin is 5%.Red and blue bars indicate positive and negative trends,respectively.Stars denote that the trend is statistically significantat the 95%confidence level.The y-axis is the linear trend;the x-axis is the percentile rank(%).The values labeled vertically are the wet-and dry-season mean precipitation intensities(mm d-1)for the period 1979–2005 at the lower bounds of each 5%percentile bin.
We furtherexamine the spatialpattern of the precipitation trendsin the wetand dry seasonsin the 20th century historical simulations.To better capture the regional features of precipitation change,the climatologicalwet-and dry-season mean precipitation values are sorted by intensity among allgrids of the models and observations.We then divide the sorted precipitation into 20 percentile bins.The interval of each percentile bin is 5%.The value in each bin is the area-weighted average of those areas having the corresponding levelof precipitation intensity.For example,the fi rst and the last binsdenote the areas w ith the lowest and highest climatological wet-ordry-season mean precipitation amount,respectively.
Figure 6 shows the corresponding precipitation trend of each bin in the wet and dry seasons.In the wet season,in both the observations and models,most regions of the world getwetter,while some regions w ith low climatologicalwetseason rainfallgetdrier.In the dry season,observationsshow a mostly significantdrying trend,except for regions w ith low climatologicaldry-season precipitation,and the amplitude of the drying tendency is comparable to the change in the wet season.However,the simulated patterns of dry-season precipitation change are different from those observed.A drying of the dry season is seen in most regions of the world in the observations.Drier dry seasons in the two models only occur in those regions w ith the lowestorhighestclimatologicaldryseason mean precipitation amount,and the trends are smaller than those of the wet season.The change in the AR distribution is similar to the change in the precipitation of the wet season(figure notshown).
3.3.Moisture budget analysis and mechanisms
In this section,to understand which specific processesare responsible for the changes of precipitation in the wet and dry seasons and the AR,we exam ine the vertically integrated moisture budget equation shown in Eq.(3).According to Eq.(3),the rainfall changes are caused mainly by the sum of changes in vertical moisture advection,horizontal moisture advection and surface evaporation.
From the climate mean state,regardless of the season, globally averaged rainfall is balanced mainly by the evaporation and verticalmoisture advection,whereas the contributions of horizontal moisture advection and the residual are relatively small(Fig.7).The results of both models indicate that the contributions of evaporation and the convergence of moisture flux(including verticaland horizontalmoisture advection)are positive in the wet season and for the AR.For dry season,however,the convergence ofmoisture flux is unfavorable for precipitation.
The time series of the moisture budget associated w ith precipitation in the wet season is shown in Fig.8.In FGOALS-g2,evaporation increases at a rate of 0.0204 mm d-1(156 yr)-1,which is statistically significant at the 1%level;vertical moisture increases at a rate of 0.0249 mm d-1(156 yr)-1,which is only statistically significant at the 10%level(Figs.8a and b,Table 1).In FGOALS-s2,evaporation and verticalmoisture advection show increasing trends of 0.0550 and 0.1675 mm d-1(156 yr)-1,both ofwhich are statistically significantat the 1%level.The horizontalmois-ture advection and the residualshow no obvious trends(Figs. 8c and d).Among the different contributions to the wetter wet–season trend,more than half comes from the verticaladvection,while the remaining contribution mainly comes from evaporation(Fig.7b).In other words,vertical moisture advection is the most important process in forming the wetter wetseason.
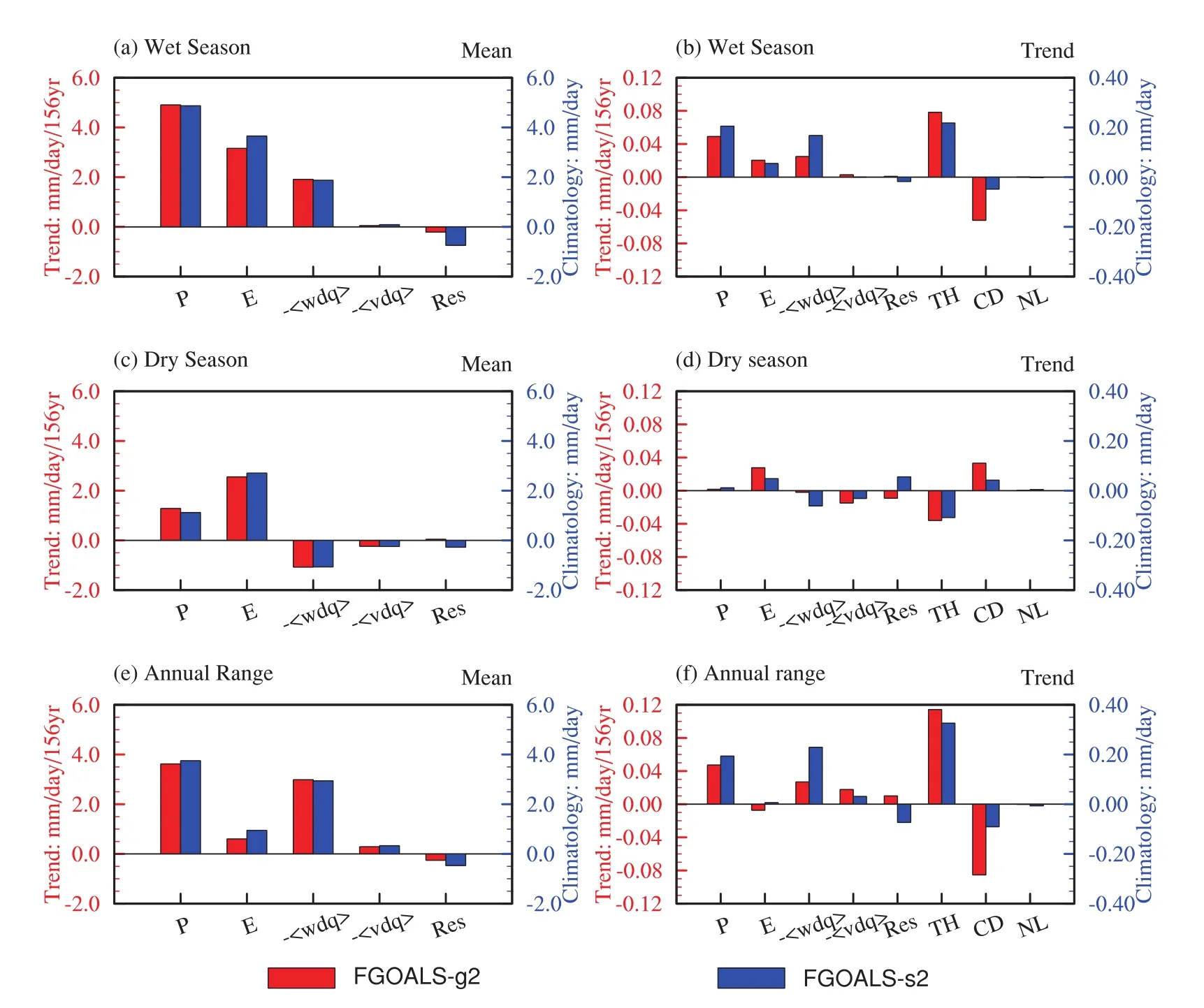
Fig.7.The(a,c,e)climatology(units:mm d-1)and(b,d,f)trends[units:mm d-1(156 yr)-1]ofglobally averaged precipitation and moisture budgetterms in the(a,b)wetseason,(c,d)dry season,and(e,f)annual range.Red(blue)coloring and the left(right)axis corresponds to FGOALS-g2(FGOALS-s2).
We further exam ine the changes in the thermodynam ic and dynam ic components,i.e.the fi rst and second terms on the right of Eq.(4).The thermodynam ic and dynam ic components are closely correlated to the precipitable water and vertical pressure velocity.The change in precipitable water vapor and vertical velocity at 500 hPa are also diagnosed.Both the watervaporand the verticalpressure velocity show significantly upward trends(Figs.8g and h),indicating that globally averaged water vapor increases and the circulation weakens as the global climate warms up.As a result, the thermodynamic componentshows a significantly positive trend at a rate of 0.0783 mm d-1(156 yr)-1in FGOALS-g2 and 0.2180 mm d-1(156 yr)-1in FGOALS-s2,while the dynam ic componentshows a significantly negative trend of-0.0521(-0.0483)mm d-1(156 yr)-1in FGOALS-g2 (FGOALS-s2)(Figs.8e and f,Table 1).In other words, increasing moisture(thermodynam ic mechanism)dom inates overweakening circulation(dynam ic mechanism)in changes of precipitation,which is consistent w ith results in previous studies(Chou and Lan,2012;Chou etal.,2013;Huang etal., 2013;Held and Soden,2006).

Fig.8.Time series(1850–2005)of the different terms in the vertically integrated moisture budgetequation for the wetseason:(a)evaporation;(b)verticalmoisture advection;(c)horizontalmoisture advection;(d) residual term;(e)thermodynam ic contributor;(f)dynam ic contributor;(g)precipitable water vapor;(h) pressure velocity at500 hPa.All time series are anomalies relative to the base period of 1850–2005.The units are mm d-1in(a–f),kg kg-1in(g),and 10-2Pa s-1in(h).The linear fi ts for allvariables are also included.The red(blue)lines represent the historical run by FGOALS-g2(FGOALS-s2).The left(right) axis correspond to the results of FGOALS-g2(FGOALS-s2).

Table 1.Trends of globally averaged precipitation and moisture budget terms.Trends thatare statistically significantat the 1%levelare marked in bold font and w ith an asterisk.Units are mm d-1(156 yr)-1.Climatological norms are given in parentheses and units are mm d-1.
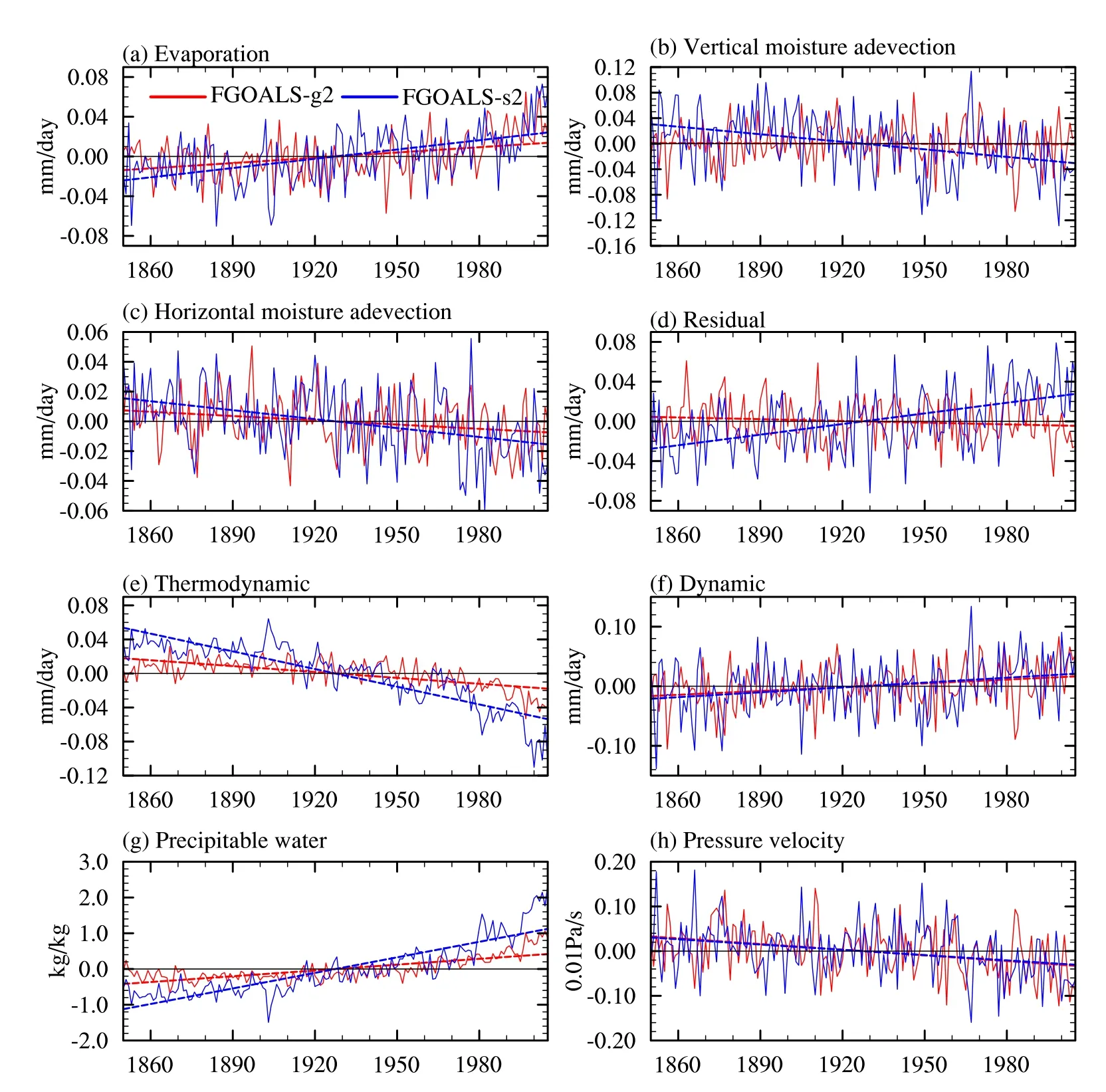
Fig.9.As in Fig.8 except for the dry season.
The contribution ofeach term to the watervaporbudgetis furtheraddressed in Fig.9.In the dry season,in both models, evaporation shows a significantly increasing trend,whereas the two moisture advection terms show a negative trend.The trend magnitude of horizontal moisture advection is comparable to that of the vertical moisture advection(Table 1).In the dry season,the vertical velocity is governed by descending motion.The verticalmoisture advection contributes negatively to precipitation changes.In the two models,water vapor shows a weaker upward trend than that in the wetseason,while the weakening trend ofdescending motion isequivalent to thatin the wetseason.Accordingly,the change tendency of the thermodynam ic(dynam ic)component is downward(upward).The opposite trends between the evaporation(positive)and the moisture advection(negative)lead to a weak and insignificantchange of precipitation in the dry season in the two models(Fig.7d).
The change of the AR is dom inated by the verticalmoisture advection(Fig.7e).A significantpositive trend is seen in the verticalmoisture advection term(Fig.10).The effects of the horizontalmoisture advection are stronger than those in the wetand dry seasons.In both models,the positive trends ofverticalmoisture advection and horizontalmoisture advection combine to enhance the AR.The evaporation trends in the wet and dry seasons are nearly identical,and thus the contribution of evaporation to the enhanced AR is negligible.Therefore,the AR change is dominated by the vertical moisture advection.The trends of the thermodynamic and dynam ic components in the wetseason are opposite to those in the dry season,and so the trend amplitudes ofboth the thermodynam ic and dynam ic components for the AR are larger than their corresponding trends in the wetand dry seasons.
The above analyses demonstrate that the seasonalprecipitation changes are dom inated by both the vertical moisture advection and evaporation terms.The contribution of the thermodynamic component is the most important term.

Fig.10.Time series(1850–2005)of the different terms in the vertically integrated moisture budgetequation for the annual range of precipitation:(a)evaporation;(b)vertical moisture advection;(c)horizontal moisture advection;(d)residual term;(e)thermodynamic contributor;(f)dynamic contributor.All time series are anomalies relative to the base period of 1850–2005.A llunits are mm d-1.The linear fi ts for all variables are also included.The red(blue)lines represent the historical run by FGOALS-g2(FGOALS-s2). The left(right)axis correspond to the results of FGOALS-g2(FGOALS-s2).
4.Summary and discussion
4.1.Summary
The change of precipitation under global warm ing has been a usefulmetric for gauging modelperformance.In this study,the performances of two versions of the LASG/IAP’s model FGOALS in reproducing the observed climatological mean state and changes of seasonal precipitation are evaluated.The mechanisms responsible for seasonal precipitation change are discussed.The analysis is carried out using the outputs of the 20th century(1850–2005)historical climate simulation experiments.The main conclusions are summarized below:
(1)Both versions of FGOALS reasonably reproduce the mean-state features of the tim ings of the wetand dry seasons, although a delayed occurrence of the wet and dry seasons is seen in the simulations in comparison to those of the observations.
(2)The climatology of precipitation in the wet and dry seasons and the AR are reproduced reasonably by bothFGOALS-g2 and FGOALS-s2.In the wet season,the PCC between the simulation and observation is 0.84(0.83),the corresponding SDR is 1.10(1.11)and the RMSD is 2.03 (2.11)for FGOALS-g2(FGOALS-s2).In the dry season, the PCC,SDR and RMSD is 0.84(0.78),1.00(1.16)and 0.86(1.11)for FGOALS-g2(FGOALS-s2),respectively.The PCC,SDR and RMSD values of the AR are 0.88,1.11 and 1.78(0.88,1.09 and 1.79)for FGOALS-g2(FGOALS-s2), respectively.
(3)The observed globally-averaged precipitation over 1979–2012 shows a significant increasing(decreasing)tendency at a rate of 0.2576(-0.1699)mm d-1(34 yr)-1in the wet(dry)season.The AR enhances at a rate of 0.4275 mm d-1(34 yr)-1.The models’responses are consistent w ith that in the observations,and both models reproduce a wetter wet season[0.0491(0.2051)mm d-1(156 yr)-1for FGOALS-g2(FGOALS-s2)]and enhanced AR[0.0474 (0.1936)mm d-1(156 yr)-1for FGOALS-g2(FGOALS-s2)] over 1850–2005.Meanwhile,wetter wetseasons and an enhanced AR are seen in most regions of the world.The weakness of the simulation is that both models show a tendency of the dry season getting wetter,which is contrary to that in the observations.However,the observational data still contain uncertainties.Whether or not the difference results from model lim itation or data quality deserves further study.
(4)Diagnoses on the outputs of the 20th century historical climate simulations of FGOALS-g2 and FGOALS-s2 show that the globally averaged seasonalprecipitation changes are dom inated by the changes of evaporation and verticalmoisture advection. In the wet and dry seasons,evaporation contributes positively to precipitation change.For the AR changes,the contribution of evaporation is negligible.The verticalmoisture advection term is the most important contribution to the changes of precipitation,wherein the thermodynam ic component is dom inant.The dynam ic component tends to compensate for the effectof the thermodynam ic component.
4.2.Discussion
Evaporation is an important process in the global water cycle(Held and Soden,2006).Solar radiation hits the surface of water or land and causes water to change state from a liquid to a gas,leading water vapor to enter the atmosphere. The moisture in the atmosphere is linked to cloud formation and rainfall(Trenberth et al.,2003).Evaporation is one of the main water vapor sources of precipitation.One consequence of increased heating from the human-induced greenhouse effect is the increased evaporation of surface moisture(Yu and Weller,2007).Thus,during 1850–2005,the response to global warm ing,regardless of whether for the wet season or dry season,the evaporation simulated by both versions of FGOALS exhibits a significantly increasing trend and then further facilitates the increase of precipitation.As the moisture supply for precipitation locally does not completely come directly from evaporation,some of it has to come from transport remotely and thus from convergence of low-levelmoisture elsewhere in the atmosphere(Trenberth et al.,2003).Meanwhile,the occurrence of the wet and dry seasons varies from grid to grid and year to year.So,as shown in our analysis,vertical moisture advection,which is closely connected w ith the low-level convergence of moisture,largely contributes to the change of global mean wetand dry-season precipitation.
In the wet season,evaporation and verticalmoisture advection combine to positively contribute to the formation of wetter wet seasons.In the dry season,the atmospheric circulation is dom inated by lower-level divergence and vertical descending motion.Although evaporation in the dry season in both models shows increasing trends equivalent to that in the wetseason,the cancellation effectof the verticalmoisture advection(negative trend)results in an unobvious change of dry-season precipitation.As the increasing trends of evaporation are roughly equivalent in the wetand dry seasons,the enhancementof the ARmainly comes from the positive trend of verticalmoisture advection.
The wet(dry)season is a period when floods(drought) occur frequently.The increased wet-season precipitation in the observations and simulations of the two versions of FGOALS may enhance the risk of floods,while the observed reduction of dry-season precipitation may enhance the risk of droughts.
Acknow ledgements.This work was jointly supported by the National Natural Science Foundation of China(Grant Nos. 41125017 and 41330423).We thank the two anonymous reviewers for theirvaluable comments on the manuscript.
REFERENCES
Adler,R.F.,and Coauthors,2003:The Version 2 GlobalPrecipitation Climatology Project(GPCP)monthly precipitation analysis(1979–present).Journal of Hydrometeorology,4,1147–1167.
Andrews,T.,P.M.Forster,O.Boucher,N.Bellouin,and A. Jones,2010:Precipitation,radiative forcing and global temperature change.Geophys.Res.Lett.,37,L14701,doi: 10.1029/2010GL043991.
Allan,R.P.,and B.J.Soden,2008:Atmospheric warming and the amplification of precipitation extremes.Science,321,1481–1484,doi:10.1126/science.1160787.
Allan,R.P.,B.J.Soden,V.O.John,W.Ingram,and P.Good, 2010:Currentchanges in tropicalprecipitation.Environmental Research Letters,5(2),025205,doi:10.1088/1748-9326/ 5/2/025205.
Bao,Q.,and Coauthors,2013:The Flexible Global Ocean-Atmosphere-Land System Model, Spectral Version 2: FGOALS-s2.Adv.Atmos.Sci.,30,561–576,doi: 10.1007/s00376-012-2133-9.
Boer,G.J.,1993:Climate change and the regulation of the surface moisture and energy budgets.Climate Dyn.,8,225–239.
Chadw ick,R.,I.Boutle,and G.Martin,2013:Spatial patterns of precipitation change in CM IP5:Why the rich don’tget richer in the tropics.J.Climate,26,3803–3822.
Chen,X.L.,T.J.Zhou,and Z.Guo,2014:Climate sensitivities of two versions of FGOALS model to idealized radiative forcing.Science China:Earth Sciences,57,1363–1373.
Chou,C.,and J.Neelin,2004:Mechanisms ofglobalwarming impacts on regional tropicalprecipitation.J.Climate,17,2688–2701.
Chou,C.,and C.Lan,2012:Changes in the annual range of precipitation under globalwarm ing.J.Climate,25,222–235.
Chou,C.,J.Neelin,C.Chen,and J.Tu,2009:Evaluating the“richget-richer”mechanism in tropicalprecipitation change under globalwarm ing.J.Climate,22,1982–2005.
Chou,C.,J.C.H.Chiang,C.W.Lan,C.H.Chung,Y.C.Liao, and C.J.Lee,2013:Increase in the range between wet and dry season precipitation.Nature Geoscience,6,263–267.
Flato,G.,and Coauthors,2013:Evaluation of climate models.Climate Change 2013:The PhysicalScience Basis.Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change,Cambridge University Press,Cambridge,United Kingdom and New York, NY,USA,741–866.
Held,I.M.,and B.Soden,2000:Water vapor feedback and global warming.Annual Review Energy and the Environment,25, 441–475.
Held,I.M.,and B.J.Soden,2006:Robust responses oh the hydrologicalcycle to globalwarming.J.Climate,19,5686–5699.
Huang,P.,S.P.Xie,K.Hu,G.Huang,and R.Huang,2013:Patterns of the seasonal response of tropical rainfall to global warming.Nature Geoscience,6,357–361.
Li,L.,and Coauthors,2013: The Flexible Global Ocean-Atmosphere-Land System Model,Grid-point Version 2: FGOALS-g2.Adv.Atmos.Sci.,30,543–560,doi:10.1007/ s00376-012-2140-6.
Li,H.,A.Dai,T.Zhou,and J.Lu,2010:Responses of East Asian summer monsoon to historical SST and atmospheric forcing during 1950–2000.Climate Dyn.,34,501–514.
Noake,K.,D.Polson,G.Hegerl,and X.Zhang,2012:Changes in seasonal land precipitation during the latter twentieth-century. Geophys.Res.Letts.,39,doi:10.1029/2011GL050405.
Pal,I.,B.T.Anderson,G.D.Salvucci,and D.J.Gianotti,2013: Shifting seasonality and increasing frequency of precipitation in wet and dry seasons across the U.S.Geophys.Res.Letts., 40,4030–4035,doi:10.1002/grl.50760.
Polson,D.,G.C.Hegerl,X.B.Zhang,and T.J.Osborn,2013: Causes of robustseasonal land precipitation changes.J.Climate,26,6679–6697,doi:10.1175/JCLI-D-12-00474.1.
Pryor,S.C.,and J.T.Schoof,2008:Changes in the seasonality of precipitation over the contiguous USA.J.Geophys.Res.,113, D21108,doi:10.1029/2008JD010251.
Qian,C.,and T.Zhou,2014:Multidecadal variability of North China aridity and its relationship to PDO during 1900–2010. J.Climate,27(3),1210–1222.
Scheff,J.,and D.Frierson,2012:Twenty-fi rst-century multimodel subtropical precipitation declines are mostly m idlatitude shifts.J.Climate,25,4330–4347.
Seager,R.,N.Naik,and G.Vecchi,2010:Thermodynam ic and dynam ic mechanisms for large-scale changes in the hydrological cycle in response to global warming.J.Climate,23, 4651–4668.
Taylor,K.E.,R.J.Stouffer,and G.A.Meehl,2012:An overview ofCM IP5 and the experimentdesign.Bull.Amer.Meteor.Soc, 93,485–498.
Trenberth,K.E.,A.Dai,R.M.Rasmussen,and D.B.Parsons, 2003:The changing character of precipitation.Bull.Amer. Meteor.Soc.,84,1205–1217.
Trenberth,K.E.,2011:Changes in precipitation w ith climate change.Climate Research,47,123–138.
Vecchi,G.A.,and B.J.Soden,2007:Global warm ing and the weakening of the tropical circulation.J.Climate,20,4316–4340.
Vecchi,G.A.,B.J.Soden,A.T.Wittenberg,I.M.Held,A.Leetmaa,and M.J.Harrison,2006:Weakening of tropical Pacific atmospheric circulation due to anthropogenic forcing.Nature, 441,73–76.
Wang,B.,and Q.H.Ding,2006:Changes in global monsoon precipitation over the past56 years.Geophys.Res.Lett.,33, L06711,doi:10/1029/2005GL025347.
Wang,B,J.Liu,H.J.Kim,P.J.Webster,and S.Y.Yim,2012: Recent change of the global monsoon precipitation(1979–2008).Climate Dyn.,39(5),1123–1135.
Wang,B.,J.Liu,H.J.Kim,P.J.Webster,S.Y.Yim,and B.Xiang, 2013:Northern Hemisphere summer monsoon intensified by mega-El Ni˜no/southern oscillation and Atlantic multidecadal oscillation.Proceedings of the National Academy of Sciences of the United States of America,110(14),5347–5352.
Wentz,F.J.,L.Ricciardulli,K.Hilburn,and C.Mears,2007:How much more rain w ill global warm ing bring?Science,317, 233–235.
William,K.L.,H.T.Wu,and K.M.Kim,2013:A canonical response of precipitation characteristics to global warm ing from CM IP5 models.Geophys.Res.Letts.,40,3163–3169, doi:10.1002/grl.50420.
Wu,B.,and T.J.Zhou,2013:Relationships between the East Asian-western North Pacific monsoon and ENSO simulated by FGOALS-s2.Adv.Atmos.Sci.,30(3),713–725,doi: 10.1007/s00376-013-2103-6.
Xie,S.P.,C.Deser,G.A.Vecchi,J.Ma,H.Teng,and A.T.Wittenberg,2010:Global warm ing pattern formation:Sea surface temperature and rainfall.J.Climate,23,966–986.
Yu,L.S.,and R.A.Weller,2007:Objectively analyzed air–sea heat fluxes for the global ice-free oceans(1981–2005).Bull. Amer.Meteor.Soc.,88,527–539.
Zhang,X.,F.W.Zw ier,G.C.Hegerl,F.H.Lambert,N.P.Gillett, S.Solomon,P.A.Stott,and T.Nozawa,2007:Detection ofhuman influence on twentieth-century precipitation trends. Nature,448,461–465.
Zhang,L.X.,and T.J.Zhou,2014:An assessment of improvements in global monsoon precipitation simulation in FGOALS-s2.Adv.Atmos.Sci.,31(1),165–178,doi:10.1007/ s00376-013-2164-6.
Zhou,T.J.,and R.C.Yu,2006:Twentieth century surface air temperature over China and the globe simulated by coupled climate models.J.Climate,19(22),5843–5858.
Zhou,T.J.,Y.Q.Yu,H.L.Liu,W.Li,X.B.You,and G.Q.Zhou, 2007:Progress in the development and application of climate ocean models and Ocean-atmosphere coupled models in China.Adv.Atmos.Sci.,24(6),1109–1120,10.1007/s00376-007-1109-3.
Zhou,T.J.,L.X.Zhang,and H.M.Li,2008:Changes in global land monsoon area and total rainfallaccumulation over the last half century.Geophys.Res.Lett.,33,doi:10.1029/ 2008GL034881.
Zhou,T.J.,D.Y.Gong,J.Li,and B.Li,2009:Detecting and understanding the multi-decadalvariability of the East Asian Summer Monsoon-Recentprogress and state ofaffairs.Meteorologische Zeitschrift,18,455–467.
Zhou,T.J.,F.F.Song,and X.L.Chen,2013a:Historical evolution of global and regional surface air temperature simu-lated by FGOALS-s2 and FGOALS-g2:How reliable are the model results?Adv.Atmos.Sci.,30(3),638–657,doi: 10.1007/s00376-013-2205-1.
Zhou,T.,F.Song,R.Lin,X.Chen,and X.Chen,2013b:The 2012 North China floods:Explaining an extreme rainfall event in the context of a long-term drying tendency[in“Explaining Extreme Events of 2012 from a Climate Perspective”].Bull. Amer.Meteor.Soc.,94(9),S49–S51.
Zhou,T.,Y.Yu,Y.Liu,and B.Wang,2014:Flexible Global Ocean–Atmosphere–Land System Model:A Modeling Tool for the Climate Change Research Community.Springer,Heidelberg,483 pp.
Zhou,Y.P.,K.M.Xu,Y.C.Sud,and A.K.Betts,2011:Recent trends of the tropical hydrological cycle inferred from Global Precipitation Climatology Project and International Satellite Cloud Climatology Project data.J.Geophys.Res., 116,D09101,doi:10.1029/2010JD015197.
:Ma,S.M.,and T.J.Zhou,2015:Precipitation changes in wetand dry seasons over the 20th century simulated by two versions of the FGOALS model.Adv.Atmos.Sci.,32(6),839–854,
10.1007/s00376-014-4136-x.
(Received 24 June 2014;revised 10 October 2014;accepted 29 October2014)
∗Corresponding author:ZHOU Tianjun
Email:zhoutj@lasg.iap.ac.cn
©Institute of Atm ospheric Physics/Chinese Academ y of Sciences,and Science Press and Springer-Verlag Berlin Heidelberg 2015
 Advances in Atmospheric Sciences2015年6期
Advances in Atmospheric Sciences2015年6期
- Advances in Atmospheric Sciences的其它文章
- Characterization of Organic Aerosols in Beijing Using an Aerodyne High-Resolution Aerosol M ass Spectrometer
- Dryland Expansion in Northern China from 1948 to 2008
- Numerical Simulations of Heavy Rainfallover Central Korea on 21 Sep tember 2010 Using the WRF M odel
- Projections of the Advance in the Startof the Grow ing Season during the 21st Century Based on CM IP5 Simulations
- Deep Convective Clouds over the Northern Pacific and Their Relationship w ith Oceanic Cyclones
- A Diagnostic Analysis on the Effectof the Residual Layer in Convective Boundary Layer Development near M ongolia Using 20th Century Reanalysis Data
