典型桥梁断面的二维抖振响应分析*

潘 韬 张 敏 葛耀君 赵 林

(中铁大桥勘测设计院集团有限公司1) 武汉 430056) (同济大学土木工程防灾国家重点实验室2) 上海 200092)

典型桥梁断面的二维抖振响应分析*

潘 韬1,2)张 敏1)葛耀君2)赵 林2)

(中铁大桥勘测设计院集团有限公司1)武汉 430056) (同济大学土木工程防灾国家重点实验室2)上海 200092)

通过刚体节段模型高频天平测力法，在优化谱估计参数的基础上，采用互功率谱方法对桥梁闭口箱梁断面的全部6个气动导纳函数进行识别，分析了导纳函数的变化特点；利用识别的气动力参数对闭口箱梁断面进行二维桥梁抖振分析，发现闭口箱梁取实测导纳的响应计算结果远小于导纳函数取1.0的计算值，且导纳取Sears函数的计算结果偏于保守，桥梁断面运动过程中系统阻尼的增加抑制了竖向及扭转抖振响应，在一般风洞试验中使用模拟二维二自由度的节段模型试验，其风洞试验结果应该是偏于安全的.

闭口箱梁断面；互功率谱；气动导纳；抖振响应

0 引 言

风荷载是桥梁风工程研究的先决条件，也是桥梁抗风分析精细化的关键所在.对于桥梁断面的气动力研究，经历了定常→准定常→修正准定常→非定常模型这样一个发展过程.静风荷载计算模型是一个线性定常模型[1]，抖振力作为一个线性准定常模型，气动导纳的引入将非定常模型准定常化[2]，而自激力模型是一个非定常模型[3].相对于桥梁跨度向超大规模方向发展而言，气动力的研究相对滞后.为此，桥梁断面气动力模型中各种参数的风洞试验识别理论和技术方法的研究，已成为大跨度桥梁抗风性能研究的关键技术，目前静风力系数和气动导数的研究在国内外已取得一定的研究进展，而与结构抖振力作用时频转换和空间相关性密切相关的气动导纳研究工作尚未突破流线型断面的理论框架，目前工程应用中所假定的气动导纳要么取为1.0，即不考虑流动的非定常特性和截面方向的不完全相关性，要么近似使用基于势流理论的平板气动导纳Sear函数及其Lipmann表达式[4]或Davenport经验公式[5]，而基于这2种取值的计算结果可导致一倍左右甚至更大的计算误差，从而降低大跨桥梁抗风设计风振响应的预测精度.

选取了典型桥梁闭口箱梁断面形式，通过在HD-2风洞中对刚体节段模型进行高频天平测力，采用互功率谱法识别方法分离了不同脉动分量对应的6个气动导纳，并利用实测导纳函数进行二维抖阵响应分析，得到一些有益的结论.

1 二维宽带湍流气动导纳识别

1.1 识别方法

在同时考虑2个方向脉动分量(u和w)的二维宽带湍流条件下的气动力往往是采用以Scanlan抖振力模型为基础，并利用气动导纳函数进行修正的表达方式，即

(1)

(2)

(3)

实际考虑多种因素的共同作用，通过节段模型高频天平测力试验，并采取互谱导纳识别方法[6]，利用脉动风速2个分量和3个抖振力方程之间的相关函数建立了6组方程，通过一次试验识别出全部6个气动导纳分量.

为了方便与Sears函数的气动导纳理论解进行相应的比较，根据导纳函数与抖振力谱的换算关系将识别的6个导纳函数等效地换算为3个等效气动导纳函数的表达形式(以升力为例).

(4)

1.2 识别方法验证

1.2.1 数值检验

由于二维节段模型没有空间相关性的问题，所以来流只是模拟一维随机过程.来流可看作为零均值的平稳高斯过程，对于随机过程的模拟方法一般称为Monte Carlo法[7]，即人工产生随机数的方法.

针对零均值高斯平稳各态历经一维随机过程{U(t),t∈T}的随机样本{u(t),t∈T},可采用三角级数模拟如下.

(5)

(6)

式中：φl为均匀分布于区间[0,2π]的随机相位；N为一充分大的正整数；Suu(ω)为功率谱密度函数；ωu和ωd分别为随机过程的频率上限和频率下限，即在此范围之外的Suu(ω)之值可忽略不计.

采用上述模拟方法，以《公路桥梁抗风设计规范》规定的水平及竖向风谱为模拟目标，分别生成时间步长0.2 s，时长600 s的模拟结果，根据如图2所示的模拟风谱与目标谱的比较可知两者较为吻合，表明本文脉动风模拟结果的正确性.

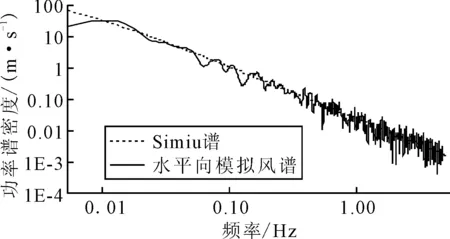
图1 模拟脉动风谱与目标函数比较

1.2.2 参数优化

根据互功率谱方法的描述，气动导纳的识别是把来流脉动风和抖振力的时域信号转化到频域内进行计算的.在此过程中，谱估计参数的优化以及谱平滑化中窗函数的选择对气动导纳识别结果有一定的影响[8]，因此需要对谱估计参数进行相应的优化和标定.

表1 虚拟节段模型参数

具体过程是先将气动导纳目标取为Sears函数，以|φsears|2Su(ω)和|φsears|2Sw(ω)为目标谱根据等效风谱法[9]生成经过导纳函数修正的脉动风时程两向分量χFuu(t)和χFww(t)时域信号，根据式(1)和表1参数生成气动力时程，通过选择多种谱估计参数，采用互谱方法来识别导纳函数分量，直到识别的导纳函数与Sears函数最为接近，即可认为该谱估计参数是最优的.

根据试验设备特点(160 Hz采样频率)和采样时间要求(60 s)，针对闭口箱梁断面模型比较了在不同来流风速(5～10 m/s)、湍流强度15%、不同风谱以及谱密度估计重叠点数512～1 536(FFT的变换总点数取4 096)等不同参数取值时的系统识别结果.气动导纳函数离散频率点数值识别结果F(ω)采用双对数坐标下的3次多项式拟合：

(7)

式中：ai为拟合参数；B为模型断面宽度；U为来流平均风速.

对于脉动风速和抖振力时程分别进行了10次随机过程模拟和导纳函数识别.限于文章篇幅，仅以5 m/s来流风速和15%湍流强度为例，用优化的谱估计参数识别出的气动导纳与Sears函数的比较见图2.

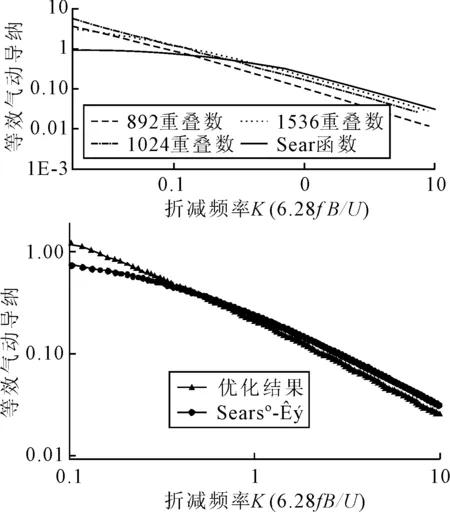
图2 5 m/s来流风速和15%湍流强度互功率谱法优化识别结果(160 Hz,60 s)

比较结果可知：气动导纳函数在双对数坐标下多项式拟合结果在低频段区间(6.28fB/U<0.1)离散性较明显，在较高频段离散性相对较小，所以气动导纳识别结果有效折减频率区域取为ωB/U≥0.1；随着谱估计重叠点数的增加，识别的导纳函数亦呈递增趋势，导纳函数的识别结果与谱估计参数取值密切相关.

通过参数优化后的识别结果(重叠点数1 536)基本与Sears函数重合，因此本文的气动导纳识别采用表2的谱估计参数，以减小气动导纳识别结果的误差.

表2 基于160Hz60s采样参数导纳函数互谱方法识别优化方案

2 模型试验

2.1 流场布置

湖南大学风工程试验研究中心的HD-2风洞为低速、单回流、并列双试验段的边界层风洞，其第一试验段长17 m，模型试验区横截面宽3 m、高2.5 m，试验段风速0～60 m/s连续可调.湍流发生装置采用宽7.5 cm、厚2.5 cm的木条编织而成，网格均为正方形，边长为22.5 cm，其在风洞中的安装见图3.

图3 风洞中的格栅及流场测点布置

通过对模型位置处的湍流风场的湍流特性测量表明各测点的湍流强度相差不大，湍流场的空间均匀性较好，可以进行试验，其平均湍流度可认为分别是Iu=0.15，Iw=0.09.

2.2 模型设计

本文设计典型的桥梁闭口箱梁断面模型，见图4，采用刚体节段模型高频天平测力法，全部模型采用轻质薄壁木质材料加工，具有足够的刚度，在试验风速作用下不会出现明显变形和振动.试验段长度为140 cm，通过设置模型端板来减小端部的边界效应影响.系统固有频率约30～35 Hz，远大于测量关心频段，满足高频测力试验要求，见图4.

图4 闭口箱梁断面

2.3 识别结果

在HD-2风洞中分别测试了4～7 m/s不同风速下模型的气动导纳.图5为模型在0°风攻角下15%湍流场中气动导纳函数随风速的变化情况.由图5可见，模型在不同风速下的气动导纳有所差别，但在不同风速下的气动导纳随折减频率的变化趋势是基本一致的.不同风速引起模型气动导纳的不同可能是受到涡脱频率的影响，随着来流风速的增加，模型的涡脱频率会逐渐增大，气动力中的涡脱力成分向高频段转移，导致所识别的气动导纳函数有一定的差别，但气动导纳随风速没有明显的趋势性变化.

图5 模型在不同风速条件下等效导纳函数结果比较(0°攻角、15%湍流强度)

表3列举了闭口箱梁模型在不同折减频率的气动导纳函数取值情况.表中折减频率的计算式中，模型自振竖弯圆频率ωh=14.04 rad/s，自振扭转圆频率ωα=28.06 rad/s，B=0.476 m，U为来流风速.由表3可见，根据闭口箱梁模型自振频率计算的折减频率区段内，实测等效导纳函数升力分量和升力矩分量的取值均小于Sears函数值.

表3 闭口箱梁模型在不同折减频率的导纳函数取值

3 二维桥梁抖振分析

3.1 抖振频域分析流程

根据抖阵频域分析方法编制了相应的分析程序，程序的步骤框图见图6.

图6 抖振频域分析程序编制框图

3.2 抖振响应分析

3.2.1 抖振结果

根据表3识别的气动导纳结果进行闭口箱梁断面的二维风振响应计算，从图7的抖振响应结果可以看出，采用实测导纳函数的抖振响小于导纳采用Sears函数的计算值，且远小于导纳函数取1.0的计算值，表明闭口箱梁导纳函数取Sears函数的计算结果是偏于保守的.

图7 闭口箱梁模型在不同风速下的抖阵响应

3.2.2 自激力的影响

以闭口箱梁节段模型为例，考虑在0°攻角下自激力对抖振响应的影响，考虑自激力的抖振计算用到的气动导数时使用了在湖南大学使用三自由度强迫振动装置识别的导数结果[10-14].

1) 首先在抖振计算中不考虑自激力的作用，仅考虑抖振力作用时的响应，然后对同时考虑抖振力和计入18个气动导数的自激力共同作用时的响应进行了计算，可以发现随着风速的逐渐增加，气动自激力的参与减小了桥梁断面的抖振位移响应，见图8.而且自激力对抖振响应的抑制作用主要是来自于气动阻尼的贡献，即桥梁断面运动过程中系统阻尼的增加抑制了抖振响应.

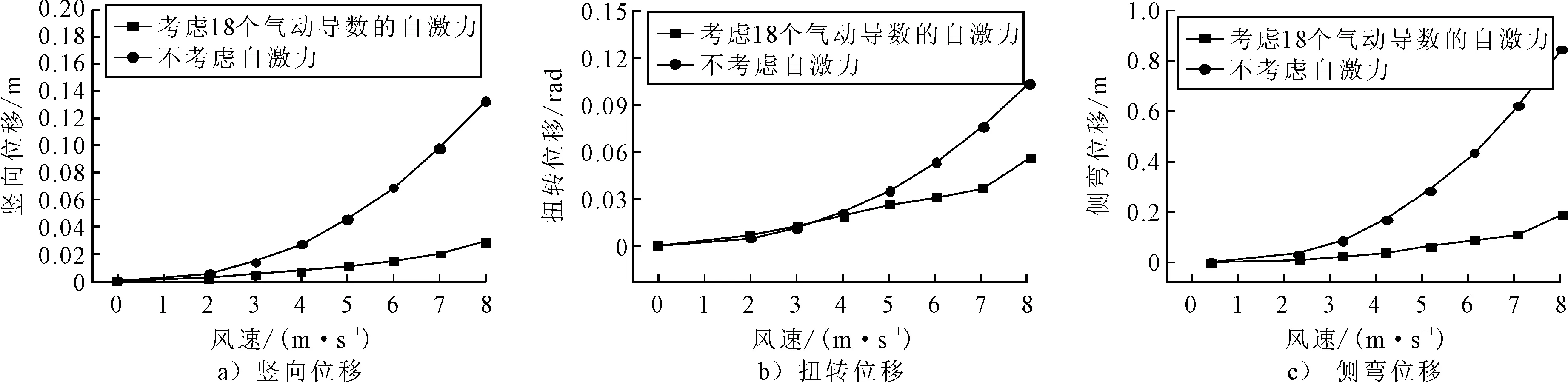
图8 考虑和忽略自激力时抖振响应的均方根值

2) 进行了二维三自由度和二维二自由的抖振响应计算，其对应的竖弯及扭转位移的抖振响应均方根值见图9.

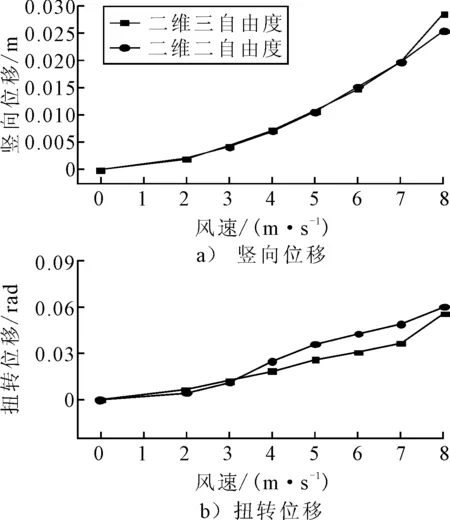
图9 二维三自由度和二自由度抖振响应的均方根值

由图9可见，考虑二维三自由度和二自由度的抖振响应，竖弯方向响应的差别很小，而对于扭转方向而言二自由度的抖振响应大于三自由度结果，很明显三自由度加入的侧向气动力对扭转有约束作用，一般风洞试验中仅使用模拟二维二自由度的节段模型试验，放弃了侧弯的模拟，其风洞试验结果应该是偏于安全的.

4 结 论

1) 互功率谱识别方法能有效识别6个导纳分量，但结果受到采样频率和谱估计参数等因素的影响，有必要采取数值验证方法对参数进行预先的优化处理.

2) 闭口箱梁模型的等效导纳升力分量和升力矩分量具有相似的形状和特征，而且它们的数值很接近，总体上呈现随折减频率递增而衰减的趋势；等效导纳阻力分量随折减频率的变化趋势都不明显，虽然总体上看是下降趋势，但变化较缓慢.

3) 闭口箱梁模型断面采用实测气动导纳的抖振响应小于导纳采用Sears函数的计算值；由于桥梁断面运动过程中系统阻尼的增加抑制了抖振响应，因此气动自激力起到减小抖振位移响应的作用；一般风洞试验中仅使用模拟二维二自由度的节段模型试验，放弃了侧弯的模拟，其风洞试验结果应该是偏于安全的.

[1]中华人民共和国交通部.JTG/T D60-01-2004公路桥梁抗风设计规范[S].北京：人民交通出版社，2004.

[2]SARKAR P P. New identification methods applied to the response of flexible bridges to wind [D]. Baltimore: Johns Hopkins University, 1992.

[3]SCANLAN R H，TOMKO J J.Airfoil and bridges deck futter derivatives[J].Journal of Engineering Mechanics，ASCE，1971,97(6):1717-1737.

[4]LIEPMANN H W.On the application of statistical concepts to the buffeting problem[J].Journal of Aeronautical Science，1952,19(12):793-800.

[5]DAVENPORT A G.The application of statistical concepts to the wind loading of structures[J]. Proceeding of the Institution of Civil Engineers，1961,19(8):449-472.

[6]靳欣华.桥梁断面气动导纳识别理论及试验研究[D].上海:同济大学,2003.

[7]李桂青,曹 宏,李秋胜，等.结构动力可靠性理论及其应用[M].北京:地震出版社,1993.

[8]薛年喜.MATLAB在数字处理信号中的应用[M].北京:清华大学出版社,2010.

[9]丁泉顺.大跨度桥梁耦合颤抖振响应的精细化分析[D].上海:同济大学,2001.

[10]潘 韬.桥梁非定常气动力模型及其风振响应分析[D].上海:同济大学,2013.

[11]张冠华，赵 林，葛耀君，等.流线型闭口箱梁断面风荷载空间相关性试验研究[J].振动与冲击，2012，31(2)：76-80，114.

[12]刘志文，胡建华，陈政清，等.闭口箱开主梁断面三分力系数二维大涡模拟[J].公路交通科技，2011，28(11)：61-66.

[13]曹丰产，项海帆，陈艾荣，等.桥梁断面的气动导数和颤振临界风速的数值计算[J].空气动力学学报，2000，18(1)：26-33.

[14]郭增伟，赵 林，葛耀君，等.基于桥梁断央压力分布统计特性的抑流板抑制涡振机理研究[J].振动与冲击，2012，31(7)：89-94，117.

Two-dimensional Buffeting Response Analysis of Typical Bridge Section

PAN Tao1,2)ZHANG Min1)GE Yaojun2)ZHAO Lin2)

(ChinaRailwayMajorBridgeReconnaissance&DesignGroupCo.，Ltd.，Wuhan430056，China)1)(StateKeyLaboratoryforDisasterReductioninCivilEngineeringofTongjiUniversity，Shanghai200092，China)2)

By using the high frequency force balance and correlation spectrum method, all the six aerodynamic admittances of box girder model were identified on the basis of the optimization of the parameters of spectral estimation. The characteristics of admittance function were analyzed. Two dimensional buffeting response of bridge box girder section were calculated by use of the identified aerodynamic parameters. It shows that the calculation results with actual admittance are far less than the value when the aerodynamic admittance replaced by one. The wind-induced responses for the big box beam model obtained conservative results when the admittance replaced by the Sears function. The system damping during the bridge section’s exercise can inhibit the vertical and torsion wind-induced response. The test results in the two degree and two-dimensional section model tests in wind tunnel should be on the safe side.

box girder model; correlation spectrum; aerodynamic admittances; buffeting response

2015-04-22

*科技部国家重点基础研究计划(973计划)项目(批准号：2013CB036300)、国家自然科学基金委重大研究计划项目(批准号：91215302)资助

U448.27

10.3963/j.issn.2095-3844.2015.03.019

潘 韬(1981- )：男，博士，工程师，主要研究领域为桥梁结构设计