基于场景概率潮流的电力系统无功优化研究

熊 强，郑永康

(1.西南交通大学电气工程学院，四川 成都 610031；2.国网四川省电力公司电力科学研究院，四川 成都 610072)

基于场景概率潮流的电力系统无功优化研究

熊 强1，郑永康2

(1.西南交通大学电气工程学院，四川 成都 610031；2.国网四川省电力公司电力科学研究院，四川 成都 610072)

多风电场出力的随机性和互相关性特点对电力系统无功优化调度有着不可忽视的影响。针对这一问题，提出一种基于场景概率潮流的电力系统无功优化方法。该方法将风电出力场景化，结合概率潮流计算，以系统有功网损、发电机无功偏差和节点电压偏差期望加权值最小作为无功优化目标函数，利用粒子群算法求得各风电出力场景下的最优无功控制策略。在含多风电场的IEEE 30节点系统中对所提方法进行测试，并与确定性的场景无功优化方法相对比，验证了所提方法的有效性。

概率潮流；场景；相关性；无功优化

0 引 言

传统的无功优化研究大多是基于确定的系统模型，假定系统中的支路参数、负荷需求、发电机出力等保持不变。但在含多风电场的电力系统中风电出力的随机性和相关性会对电力系统运行状态会产生很大的影响[1]。如若不考虑这些影响，仍采用确定性的模型对系统进行无功优化，所得到的控制策略往往不是最优的，甚至可能起到恶化的效果。鉴于此，文献[2]基于概率潮流计算方法，以网损期望值最小、电压越限概率最小和负荷裕度最大为多目标，采用粒子群算法进行了无功优化研究，但没有考虑风电场之间的相关性对无功优化的影响。文献[3]考虑了随机变量相关性，通过概率潮流计算方法对电力系统的电压稳定和无功优化问题进行了研究，但由于文献假设风速服从威布尔分布，故所得概率分析结果仅适用于系统长期或中长期评估[4]，实际参考价值有限。

针对这些问题，提出一种基于场景概率潮流的无功优化方法，建立了多风电场出力的场景概率模型，结合蒙特卡洛模拟概率潮流计算方法[5]，利用改进的粒子群算法求得各场景下的最优无功控制策略，为电力系统运行与规划人员提供丰富的决策信息。

1 场景概率潮流计算

为了考虑多风电场出力的随机性和相关性，将场景概率潮流计算引入到电力系统无功优化问题中。首先，利用K均值聚类和Copula函数[6-7]建立了多风电场出力的场景概率模型，再结合蒙特卡洛模拟法在各场景中实现了概率潮流计算。具体实现过程如下。

1)风电出力场景化。利用K均值聚类在识别数据内在结构上的优点，将原始多风电场出力数据划分为S类，并记录每一类发生概率；

2)求取风电出力边缘分布函数。采用非参数核密度估计[8]求得各场景中风电出力的边缘分布函数；

3)构建多风电场出力场景概率模型。利用Copula理论建立各场景下风电出力的联合概率分布函数；

4)场景概率潮流计算。对各场景下概率分布函数进行采样，利用蒙特卡洛模拟实现概率潮流计算；

5)系统概率评估。对概率潮流计算结果进行统计分析，得到各状态变量的统计特性及分布信息。

2 基于场景概率潮流的电力系统无功优化

以场景概率潮流计算代替传统无功优化中的确定性潮流计算，以系统有功网损、发电机无功偏差和节点电压偏差期望加权值最小作为无功优化目标函数，利用改进粒子群算法求得各风电出力场景下的最优无功控制策略。

2.1 无功优化数学模型

1) 目标函数

(1)

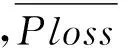
2) 等式约束条件

(2)

式(2)为系统潮流方程。

3) 不等式约束条件

(3)

式中，VGmin和VGmax分别为发电机端电压上限值和下限值；KTmin和KTmax分别为可调变压器分接头的上限值和下限值；QCmin和QCmax分别为补偿电容器投切组数的上下限值。

2.2 改进粒子群算法

(4)

Xgb(t+1)=arg{minF(Xipb(t+1))}

(5)

粒子位置向量和速度向量每一维按式(6)、式(7)更新：

(6)

(7)式中，w(t)为惯性权重；c1和c2为权系数；r1(t)和r2(t)为0到1之间的随机数；vmax为粒子最大速度；η为约束因子。

从式(6)可以看出w(t)能够平衡PSO算法的全局搜索能力和局部寻优能力，其值越大全局搜索能力较强；反之，局部搜索能力较强。在迭代初期，希望各粒子能够具有较强全局探索能力；迭代后期，则希望粒子拥有良好的局部搜索能力。为此，采用线性递减权重原则来动态调整惯性权重值[11]，见式(8)：

(8)

式中，wmax、wmin分别w最大值和最小值；Tmax为最大迭代次数。

2.3 算法流程

结合场景概率潮流和粒子群算法实现了考虑多风电场相关性的无功优化研究，具体算法流程如下。

1) 输入系统网络参数，各风电场实测出力数据；

2) 利用K均值聚类将风电场出力数据划分为L类；

3) 利用Copula函数建立各类中风电出力的联合概率模型；

4) 对各场景概率模型进行采样，得到各场景下的模拟风电出力数据，令T=1；

5) 选择场景T样本数据进行无功优化；

6) 初始化种群，设置相关参数；

7) 利用概率潮流计算得到场景T中目标函数值；

8) 根据式(4)和式(5)更新粒子的最优位置；

9) 判断是否达到最大迭代次数：是，则进行下一步；否，则按式(6)和式(7)更新粒子的速度和位置；

10) 得到场景T的最优无功控制策略，判断T=L是否成立：是，则算法结束；否则令T=T+1，转入步骤5)循环迭代。

3 算例分析

在含多风电场的IEEE30节点系统中对所提方法进行仿真测试，系统结构如图(1)所示。算例将负荷节点分为两个区域：1-15和16-30，区域内相关系数为0.9，区域间相关系数为0.5，并假设负荷随机变量服从正态分布。在节点6和9接入两个风电场，其出力数据取自两个相邻风电场的实测出力值。该系统中控制变量如表1所示。

算例中PSO算法的参数设置如下：学习因子取经典值c1=c2=2；惯性权重w(t)最大最小值分别取为0.95和0.4；约束因子η=0.729；种群数取为30，最大迭代次数为100，粒子维数为13；目标函数中惩罚因子λQ=1，λV=100。在概率潮流计算中采样规模取为500。

表2为基于场景概率潮流的电力系统无功最优控制策略，图2为各场景无功优化过程中PS0算法收敛曲线。

决策人员可根据表2根据风电出力所处的场景进行相应的调度控制。此外，从加权目标函数值可以看出，随着风电出力的增加，优化后的系统运行状态更优。图2可以看出，各场景无功优化在70代左右收敛到最优值。

表1 IEEE 30节点系统控制变量信息表

表2 场景概率模型最优无功控制策略

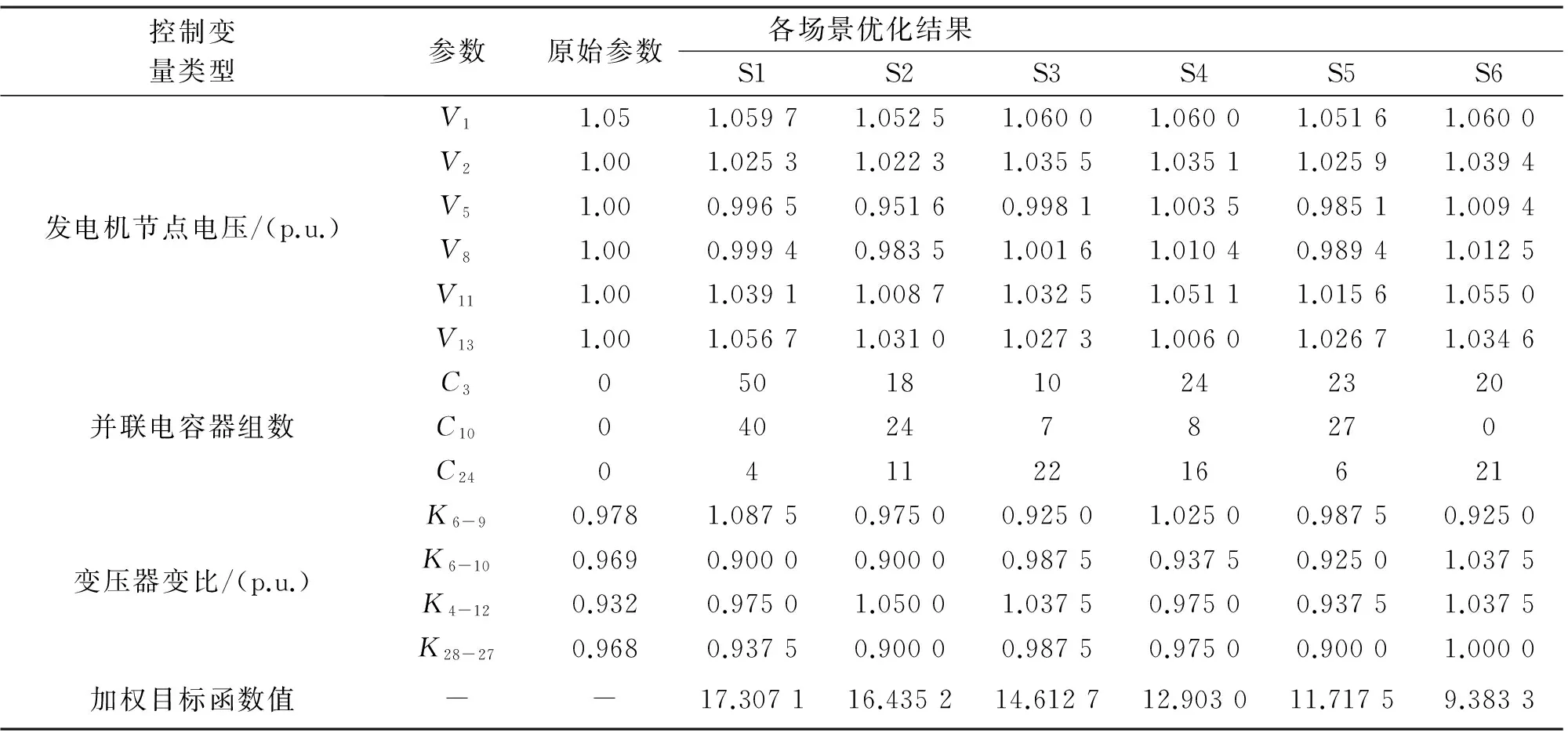
表3 确定模型最优无功控制策略

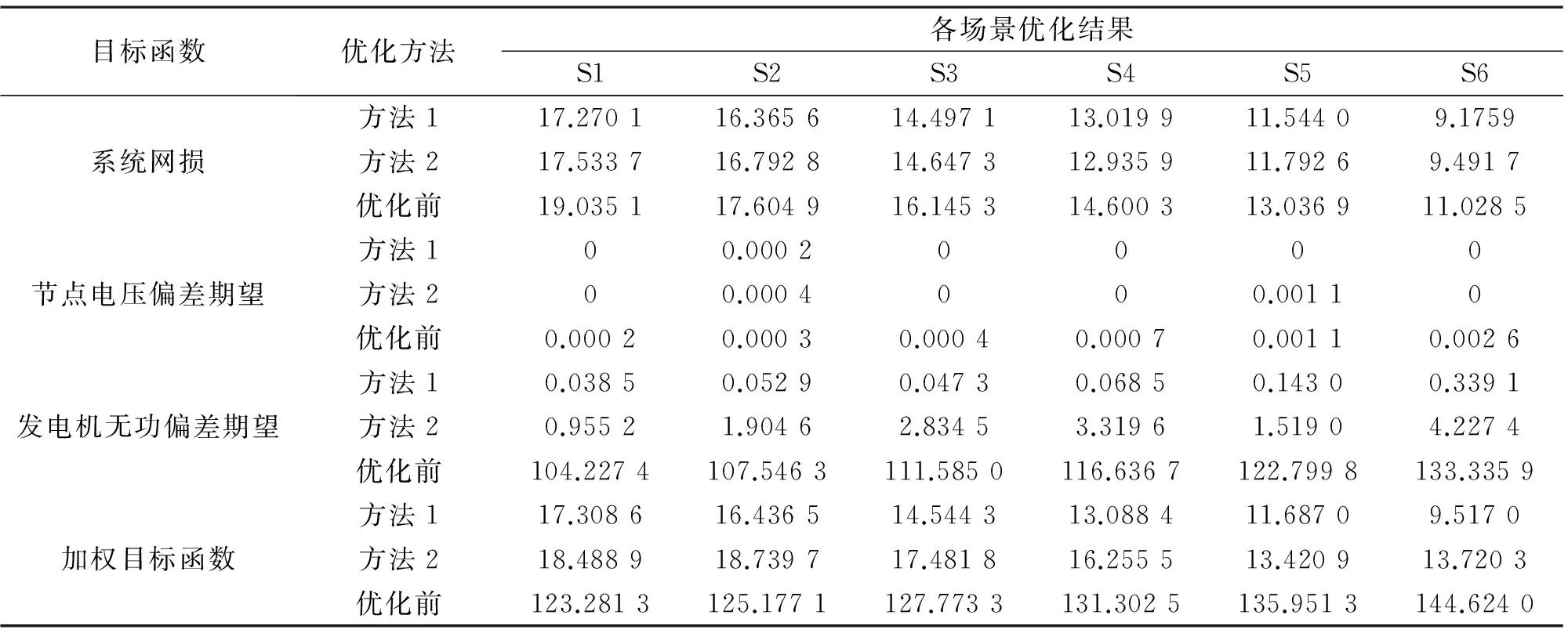
表4 不同优化方法各场景结果比较

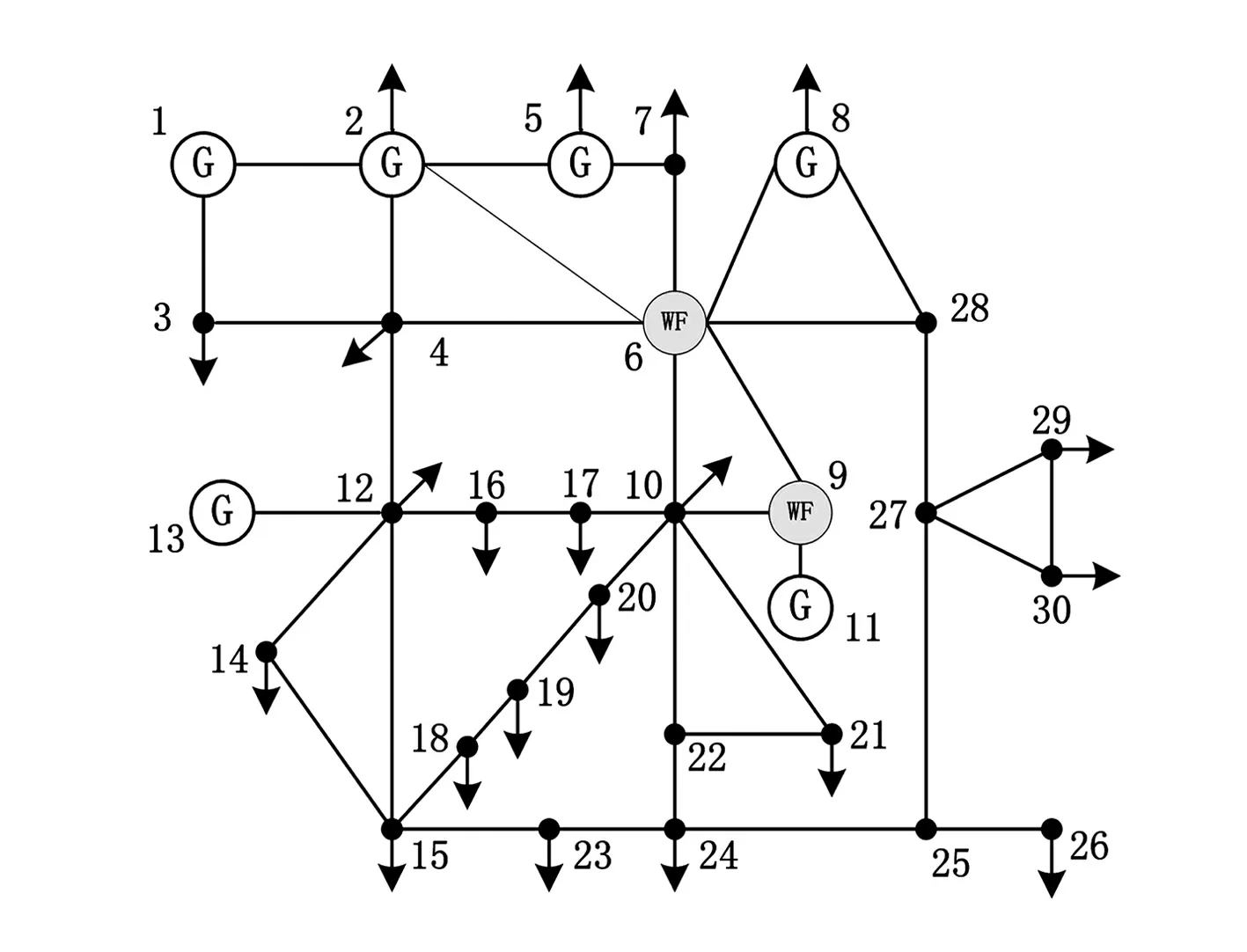
图1 含两个风电场的IEEE 30节点系统

为了验证所提方法优于传统确定性无功优化方法，将两种方法进行了对比分析：其中方法1为所提方法；方法2为传统的确定性场景无功优化方法，即不考虑系统中存在的不确定因素，将各场景中风电出力的平均值作为实际出力，代入无功优化模型，以确定性潮流计算所得适应值作为目标函数，得到各场景下的最优无功控制策略。

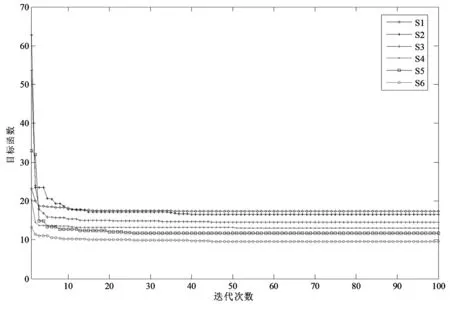
图2 各场景PSO收敛曲线

由于在实际电网运行过程中，风电出力和负荷不可能固定不变，故将方法2所得到的最优控制策略代入方法1考虑随机因素的目标函数中，将所得各场景下的适应值与方法1的结果相对比。

表3为方法2各场景最优无功控制策略；表4为两种方法对比结果。

对比表3和表4可以看出：在最优控制策略下方法1和方法2在各场景中的加权目标函数值相差都很小，个别场景方法2甚至优于方法1。从表4可以看出，在考虑风电出力随机变化时，虽然两种方法都能较大程度上实现对系统的优化，但在方法1的最优控制策略下，系统的各项指标明显优于方法2，说明方法1能够考虑系统中存在的随机变量，得到更可靠的无功优化策略。

4 总 结

将场景概率潮流计算方法应用到电力系统无功优化研究中。充分考虑了系统中负荷、风电出力的随机性和相关性，从概率的角度得到了各场景下的最优无功控制策略。与传统的确定性无功优化方法相比，所提方法在含不确定性因素的系统中表现更优，所得到的无功配置方案能够适应随机因素的变化，为运行与规划人员提供更可靠、更全面、更经济的控制策略。

[1] 潘雄, 周明, 孔晓民, 等. 风速相关性对最优潮流的影响[J]. 电力系统自动化, 2013(6):37-41.

[2] 柳杰, 刘志刚, 孙婉璐, 等. 含风电场电力系统电压稳定性概率评估及其在无功优化中的应用[J]. 电网技术, 2012(11):134-139.

[3] 李鸿鑫. 考虑不确定性因素的电力系统电压稳定与无功优化问题研究[D].武汉： 华中科技大学, 2013.

[4] 朱星阳, 刘文霞, 张建华, 等. 电力系统随机潮流及其安全评估应用研究综述[J]. 电工技术学报, 2013(10):257-270.

[5] 陈雁, 文劲宇, 程时杰. 考虑输入变量相关性的概率潮流计算方法[J]. 中国电机工程学报, 2011(22):80-87.

[6]NelsenRB.AnIntroductiontoCopulas[M].SpringerScience&BusinessMedia, 2007.

[7] 黎静华, 韦化. 基于内点法的机组组合模型[J]. 电网技术, 2007(24):28-34.

[8] 秦志龙. 计及相关性的含风电场和光伏电站电力系统可靠性评估[D]. 重庆：重庆大学, 2013.

[9] 梁艳春. 群智能优化算法理论与应用[M].北京：科学出版社, 2009.

[10] 陈前宇, 陈维荣, 戴朝华, 等. 基于改进PSO算法的电力系统无功优化[J]. 电力系统及其自动化学报, 2014,26(2):8-13.

[11]ShiY,EberhartR.AModifiedParticleSwarmOptimizer[C].IEEE,WorldCongressonComputationalIntelligence，1998.

The randomness and cross-correlation of wind farms output have a negligible impact on reactive power optimization scheduling of power system．Aiming at this problem, a reactive power optimization method based on scenario probabilistic load flow is proposed. The wind farm output is scenarized in this method. Combining with the probabilistic load flow, it takes the minimum weighted value of system network loss expectation, generator reactive power and node voltage deviation expectation as the target function and uses the particle swarm optimization to get the optimal reactive power control strategy in each scene. The proposed method is tested in IEEE 30 node system including wind farms and compared with the deterministic scenarios optimization method. The simulation results demonstrate the effectiveness of the proposed method.

probabilistic load flow; scenario; correlation; reactive power optimization

TM74

A

1003-6954(2015)03-0068-05

2015-04-07)

熊 强(1989)，硕士研究生，研究方向为电力系统及其自动化；

郑永康(1977)，博士，高级工程师，主要研究方向为继电保护。