美国南加州地区1981—2011年MW≥6.0地震前发震应力场与构造应力场趋于一致现象研究*

韩晓明 荣代潞

1) 中国呼和浩特010010内蒙古自治区地震局 2) 中国兰州730000中国地震局兰州地震研究所



美国南加州地区1981—2011年MW≥6.0地震前发震应力场与构造应力场趋于一致现象研究*

1) 中国呼和浩特010010内蒙古自治区地震局 2) 中国兰州730000中国地震局兰州地震研究所

定义了“P轴分布集中度”， 用以研究中强地震前中小地震震源机制变化． 利用美国南加州地区1981—2011年地震的震源机制解资料, 分析了该地区8次MW≥6.0地震前由小震震源机制求得的发震应力场P轴的集中情况． 结果表明， 其中7次地震前均观察到了“P轴分布集中度”值具有极小值， 即小震发震应力场P轴向区域构造应力场主压应力的集中现象， 为中强震预测提供了一种方法．

P轴分布集中度 震源机制解 美国南加州地区 发震应力场

引言

大震前震源区一定范围的小震震源机制趋于一致作为一种前兆现象得到了广泛关注(陈颙， 1978； 刁桂苓， 于新昌， 1980， 1982； 刁桂苓等， 1994)． 万永革(2008)以及Wan和Sheng(2009)利用美国南加州地区的震源机制资料， 采用Kagan(2007)提出的四元素法中计算两个地震位错模型之间差别的三维空间旋转角的方法， 分别研究了以1992年LandersMW7.3和1999年Hector MineMW7.1地震矩心为圆心的圆形区域内的地震震源机制相对于主震震源机制平均空间旋转角的变化．

地震震源机制是指震源区在地震发生时的力学过程． 由震源机制解可以得到发震应力场(即P轴、T轴和B轴)， 其受区域构造应力场的控制． 虽然地震震源机制解得到的发震应力场的主压应力P轴统计平均与构造应力方向并不完全一致(Yamakawa， 1971)， 但一定区域范围内大震(特别是M≥7.0大震)的发震应力场主压应力(P轴)的优势方向则可认为与该地区的构造应力场主压应力方向大体一致． 大震前震源区小震震源机制趋于一致实质上是在区域构造应力场的作用下， 震源区一定范围的应力集中过程． 由于震源区断层构造的复杂性， 使发生的中小地震的震源机制解也呈现复杂性， 不同小震的震源机制解(断层面走向、 倾角和滑动角)可以有相同的发震应力场主压应力主轴． 因此， 研究由震源机制解得到的小震发震应力场主压应力主轴的集中过程可以更直接地体现主震发生前震源区的应力集中过程． 王俊国和刁桂苓(2005)构造震源机制一致性参数， 研究了千岛岛弧大震前哈佛大学矩心矩张量解的一致性， 提出用震源机制与构造应力场的一致性进行地震预测的思路． 虽然该文只利用了该地区MW≥5.2的地震资料， 也没有研究每次MW≥7.5地震前震源机制一致性参数变化的时间进程． 但是从该文中也可以看出， 千岛岛弧地区MW≥5.2地震的发震应力场中，T轴比较分散， 但其所对应的P轴却相对集中(见该文中图4)． 这使我们有理由尝试仅用P轴分布的一致性来研究大震前震源机制的集中现象． 荣代潞(2014)曾利用祁连山中东段地区布设的数字地震台网获得的多年小震震源机制解资料， 研究了该地区两次中强地震前小震发震应力场主压应力P轴的集中情况．

本文将利用Yang等(2012)给出的1981—2011年美国南加州地区的地震震源机制解资料， 研究在该区域发生的MW≥6.0地震前震源区一定范围内小震发震应力场主压应力主轴的集中情况, 试图发现中强地震前小震震源机制解所表现出的前兆现象， 为中强震预测提供一种可能的方法.

1 资料和参数选择

从Yang等(2012)的地震目录中挑选出MW≥6.0地震8次． 对于这8次地震的参数， 不同数据来源不尽相同(Freedetal， 2007； Global CMT， 2012; Yangetal， 2012)， 我们选用哥伦比亚大学全球矩心矩张量解目录(Global CMT， 2012)给出的地震参数， 如表1所示， 其震中分布见图1．

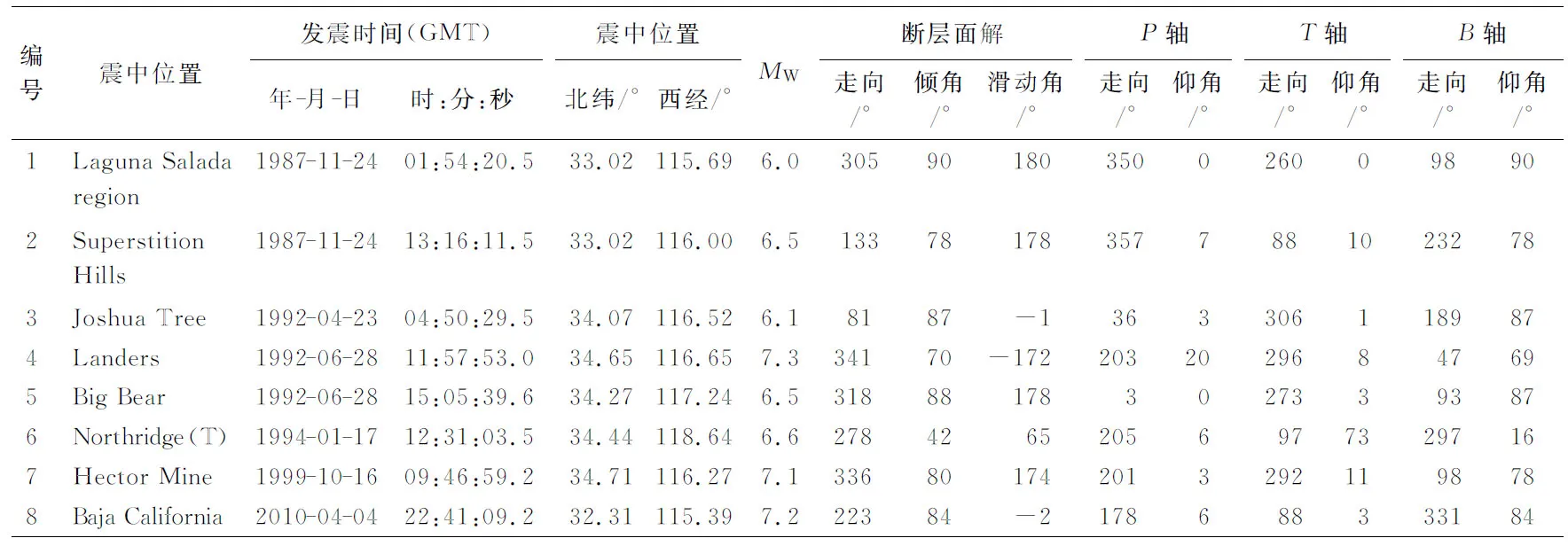
表1 本文所选取的8次MW≥6.0地震参数(引自Global CMT， 2012)

注： 震中位置参考了Freed 等(2007)结果, 发震应力场数据根据断层面解计算得出．

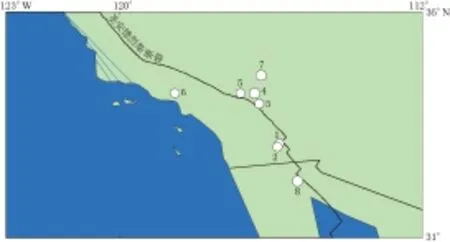
图1 本文所选取的1981—2011年美国南加州地区MW≥6.0地震分布 (据Global CMT， 2012). 图中地震编号与表1中编号相对应

选择主震发生前5年为起始时间， 以主震震中为圆心, 分别以250， 200， 150， 100 和50 km为半径选取Yang等(2012)一文中的小震震源机制解资料．

Yang等(2012)的地震目录中的震源机制解是利用台站记录的初动符号与振幅比(S/P)得出的， 因此， 小地震震源机制解的可靠性相对较低. 另外， 由于所利用的地震记录的完备性也会影响统计的精确度， 所以我们对每一次主震均利用古登堡公式检查该地震目录的完备性． 结果表明： 表1中1—7号地震记录的完备性较好， 最小震级取为M1.5； 8号地震的最小震级取为M2.0．

2 分析方法

本文采用由地震震源机制解计算得出的发震应力场的P轴方位角作为分析的目标参数， 分析中未考虑P轴的仰角. 对于仰角不为零的P轴， 可以理解为P轴在水平面的投影． 由于P轴可向两个方向延伸， 因此可将位于相差180°方向的P轴视为同一方向． 具体处理时， 若某一地震P轴方位角φ1=30°， 另一地震P轴方位角φ2=215°， 在考虑向NE向主压应力方向φ0=5°集中时，φ1与φ0的夹角取α1=25°，φ2与φ0的夹角取α2=30°， 如图2所示．

图2 计算“P轴分布集中度”的示意图Fig.2 The schematic diagram for calculating the concentration ratio of P axis distribution

在前人研究的基础上， 本文定义了一种新的参数“P轴分布集中度”， 用以研究主震前小震发震应力场的动态变化， 旨在探索一种较为简单直观的震前小震发震应力场变化的分析方法．

由一次地震的震源机制解得到的应力场(P轴，T轴等)为该地震的发震应力场， 其与构造应力方向并不完全一致， 通常受构造应力场和区域构造控制． 由于应力场大小的绝对值测定比较困难， 因此目前研究大多集中在应力场方向的变化上， 认为大震前小震震源机制趋近主震震源机制的现象， 在一定程度上代表了应力方向集中于产生主震破裂的应力方向上． 以往通常使用的P轴分布玫瑰图只能表示P轴方位的空间分布， 并不能显示P轴的动态变化， 即在孕震过程中P轴方位随时间的变化． 本文所定义的新参数“P轴分布集中度”， 则可用以研究主震前小震发震应力场的动态变化．

众所周知， 在数学中一组数据(数据集)的标准差能反映该数据集的离散程度． 借用这一概念， 对于选定的第i个地震序列和一个应力场方向(可以是主震发震应力场的主压应力场， 或是构造应力场)， 计算该地震序列中每次地震P轴方位角与给定应力场方向之差(图2)， 从而构成一个数据集． 该数据集的标准差即反映其离散程度, 具体计算公式为

(1)

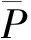
对于不同的地震序列， 其所构成的数据集的平均值是不同的． 为消除不同平均值的影响， 使用标准差与平均值的比值， 即所谓的“相对标准差”定义本文的“P轴分布集中度”：“P轴分布集中度”c值越小， 表示小震震源机制发震应力场P轴向给定的应力场方向集中的程度越高．

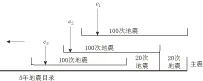
图3 “P轴分布集中度”ci的时间演化分析示意图Fig.3 The schematic diagram for temporal evolution of “concentration ratio of P axis distribution” ci

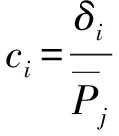
(2)

计算“P轴分布集中度”的空间窗为主震震中周围一定半径的圆形区域， 时间演化用下面的方法计算(图3)． 选取地震序列的时间间隔始于主震发震时刻， 向前止于某一时刻； 然后使用一个按一定步长移动的滑动时间窗． 我们参照Zöller等(2001)选取滑动时间窗的方法， 没有固定时间窗的长度， 而是使用包含相同数量地震的时间窗． 本文中每一个时间窗包含100次地震， 按20次地震的步长滑动． 对于某些主震由于在空间窗内半径较小(50km)， 所包含的地震较少， 则选取时间窗包含60次地震， 滑动步长为10次地震． 计算结果表明， 即使时间窗和滑动时间窗所包含的地震数目发生变化， 其结果也是相对稳定的．

由此形成一个主震前小震震源机制“P轴分布集中度”ci随时间变化的序列． 这里顺便指出， 由于用地震次数来定义时间窗， 因而在时间轴上ci的分布是不均匀的．

在以往关于大震前地震震源机制集中的讨论中， 一些观点认为震源机制集中于主震震源机制， 另一些观点则认为震源机制集中于区域构造应力场． 在一些情况下这二者是一致的， 但也存在主震震源机制得到的发震应力场与区域构造应力场相差较大的情况． 本文中除了分析震源机制集中于主震的发震应力场外， 同时也分析震源机制集中于构造应力场的情况， 以期得到较为明确的结论．

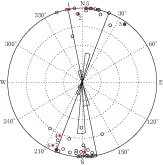
图4 美国南加州地区MW≥6.0地震的P轴分布空心圆代表地震P轴， 星形代表表1中所列的地震， 数字代表地震编号Fig.4 P axis distribution of the earthquakes with MW≥6.0 in southern California Open circles represent P axis of the earthquakes, solid circles represent the earthquakes in Table 1, and the figures show the serial number of earthquakes

3 美国南加州地区构造应力场

一些研究利用发生的大地震研究了美国南加州地区的构造应力场(Hardebeck， Hauksson, 2001; Freedetal, 2007)． 虽然单次大震的发震应力场与区域应力场并不完全一致， 但是在某一区域发生的多次大地震的发震应力场优势方向与区域构造应力场基本是一致的． 本文收集了研究区域MW≥6.0地震的震源机制解资料(Hardebeck， Hauksson, 2001; Freedetal, 2007; Globle CMT， 2012)， 得到其P轴分布， 如图4所示．

图4中玫瑰图表示P轴的空间分布， 大致在350°—20°之间(图中两条直线所夹的区域)， 接近水平方向； 优势方向大致在355°—10°之间， 也就是说， 研究区的构造应力场方向接近N--S方向的水平主压应力方向．

4 计算结果

对于表1中所列的8次主震， 我们分别计算了以震中为圆心， 半径为250， 200， 150， 100和50 km范围内， 从主震开始向前5年内所发生的地震发震应力场的“P轴分布集中度”， 所给定的应力集中在主震发震应力场方向和7个区域应力场方向(350°, 355°, 0°, 5°, 10°, 15°， 20°), 结果如图5—8所示． 表2列出了c值减小的时间段以及c值最小值距主震发生的时间.

从图7可以看出， 6号地震主震前“P轴分布集中度”没有出现明显的极小值． 究其原因， 该地震发生在海边， 而Yang等(2012)地震目录中的震源机制解是利用台站记录的初动符号与振幅比(S/P)得出的， 因此我们可以推测， 该地震震源区及附近发生的小震由于记录台站分布的限制， 其震源机制解的可靠性可能受到质疑． 当空间范围扩大至250 km时， 包含了1992年发生的3次地震(3, 4和5号地震)， 因此“P轴分布集中度”出现了极小值， 如图7中6号地震中黑色曲线和黑色箭头所示．

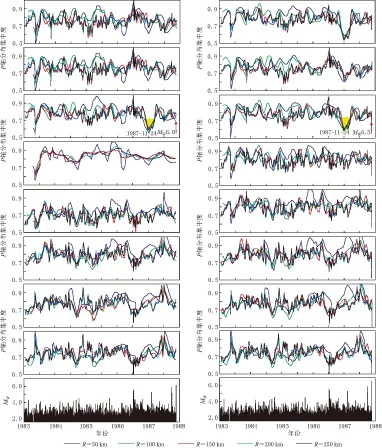
图5 美国南加州地区1号(左)和2号(右)地震“P轴分布集中度”计算结果

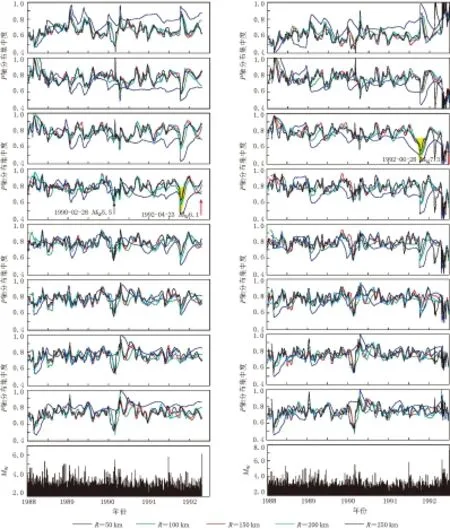
图6 美国南加州地区3号(左)和4号(右)地震“P轴分布集中度”计算结果. 图中说明同图5

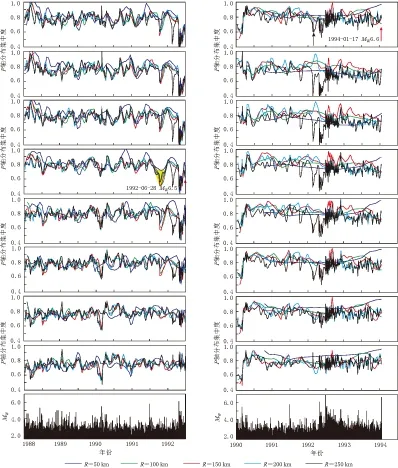
图7 美国南加州地区5号(左)和6号(右)地震“P轴分布集中度”计算结果. 图中说明同图5

从给定的不同应力场P轴(主震的发震应力场P轴和NNE10°—20°)的计算结果可知， 7次地震对区域应力场P轴的优势方向均表现出明显的集中， 其中3， 4和7号地震对主震发震应力场没有明显的集中现象， 究其原因可能是由于这3次地震的发震应力场P轴与区域应力场相差较大(分别为36°， 203°和201°)所致． 1号和2号地震发生在同一天且震中距相差很小， 其P轴走向相差不大(360°和357°)且与区域应力场优势方向基本一致， 故与主震应力场集中情况吻合较好． 而4号和5号地震虽也发生在同一天， 震中距约为35 km， 但其发震应力场相差较大(分别为203°和3°)， 所以与主震应力场的集中情况有较大差别． 5号地震的P轴与区域应力场基本一致， 故震前小震P轴对主震应力场集中的“P轴分布集中度”具有极小值． 由此我们可以得出结论， 主震前小震P轴集中实质上是震源区的应力场在构造应力场的作用下向区域构造应力场集中．

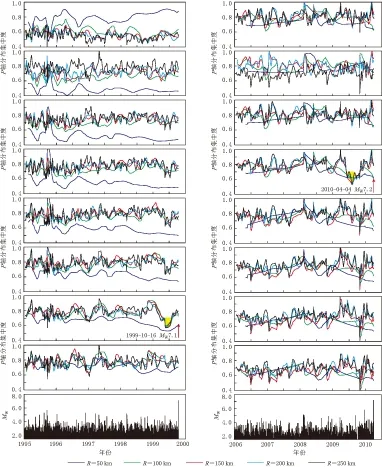
图8 美国南加州地区7号(左)和8号(右)地震“P轴分布集中度”计算结果. 图中说明同图5

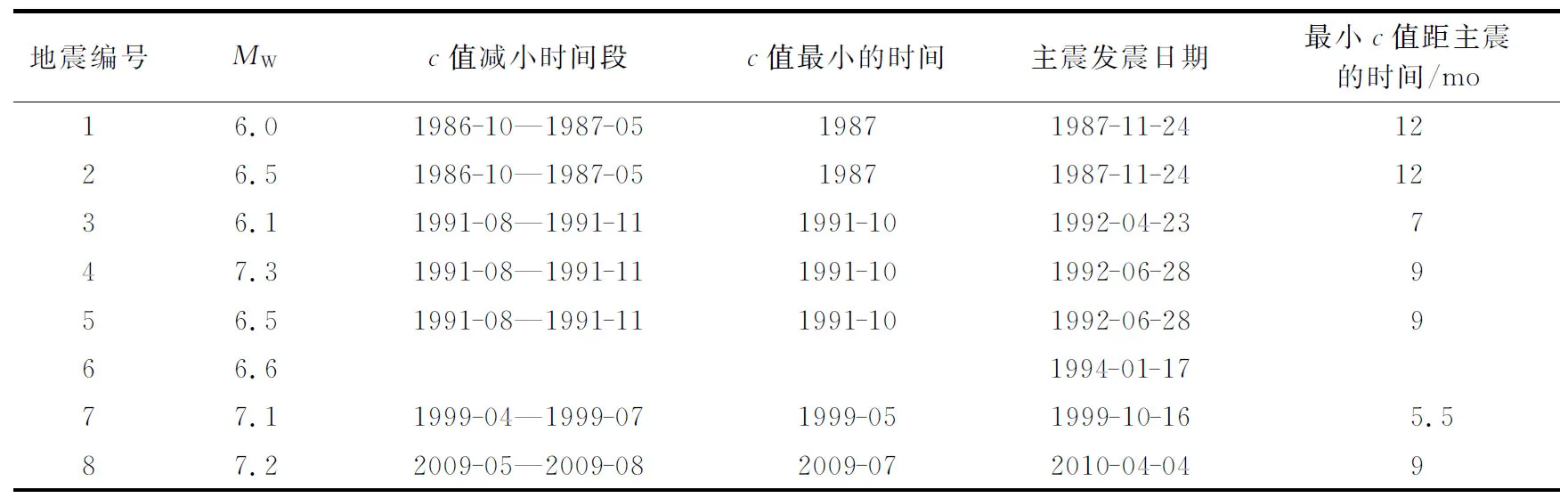
表2 “P轴分布集中度”c值减小的时间段以及c值最小值距主震发生的时间

从图5—8可以看到， 对于不同的空间半径， 大多数情况下在c值出现极小值的时段， 不同空间半径均同时出现极小值， 只是各极小值的大小有差别． 对于半径为50 km的范围， 可能由于有的主震地震数量较少， 其c值变化出现“异常”， 即其可靠性较低． 不过从各个曲线的总体变化趋势来看： 对于MW=6.0—6.5地震， 其“P轴分布集中度”c值减小最为明显的区域范围为100—150 km； 对于MW≥7.0地震， “P轴分布集中度”c值减小最为明显的区域范围为150—250 km. 这与地震越大, 可能的前兆范围越大的认识是一致的.

本文研究的是MW≥6.0地震， 在图5—8中对照“P轴分布集中度”与主震周围地震的M-t图可以发现, 在一些MW5.0左右的地震前也有类似的“P轴分布集中度”出现极小值的情况， 例如1990年2月28日MW5.5地震， 如图6中3号地震中黑色箭头所示．

5 讨论与结论

本文中所研究的美国南加州地区所发生的8次MW≥6.0地震中， 除6号地震外， 其余7次地震在主震前某段时间均出现了“P轴分布集中度”c值减小的现象，c值极小值出现在主震前半年至一年内． 在c值极小值出现后， “P轴分布集中度”又逐渐增加， 直至主震发生． 这可能是由于c值极小值出现后研究区域发生的一些小震释放了部分应力， 使应力集中程度有所降低的缘故．

综上所述， 本文得出的初步结论如下：

1) 本文定义的“P轴分布集中度”能较好地反映主震前小震发震应力场P轴的集中情况， 且物理意义明确， 计算简便；

2) 在美国南加州地区发生的几次MW≥6.0地震前， 均观察到“P轴分布集中度”具有极小值的现象， 这说明它可能是中强地震前所表现出的一种前兆现象；

3) 主震前小震发震应力场P轴的集中是集中到震源区的区域构造应力场主压应力场方向， 这给中强地震的预测提供了一种可能的方法． 以往的研究主要致力于震源机制集中到主震震源机制上， 而主震发生前主震的震源机制是未知的． 一个地区的区域构造应力场可以用很多方法估算得到， 因此可以根据一个地区地震活动的资料计算其震源机制的发震应力场对区域构造应力场的集中情况， 以此来追踪该地区大震发生的危险性．

本文中由震源机制断层面解计算发震应力场的过程中使用了许力生研究员编制的MATLAB程序， 谨表谢意．

陈颙. 1978. 用震源机制一致性作为描述地震活动性的新参数[J]. 地球物理学报, 21(2): 142--159.

Chen Y. 1978. Consistency of focal mechanism as a new parameter in describing seismic activity[J].ActaGeophysicaSinica, 21(2): 142--159 (in Chinese).

刁桂苓, 于新昌. 1980. 唐山地震前后京、 津、 唐、 张地区的综合断层面解[J]. 西北地震学报, 2(3): 39-47.

Diao G L, Yu X C. 1980. The composite fault-plane solutions in Beijing-Tianjin-Tangshan area before and after Tang-shan earthquake[J].NorthwestSeismologicalJournal, 2(3): 39--47 (in Chinese).

刁桂苓, 于新昌. 1982. 海坨山地震前综合断层面解矛盾比的变化[J]. 地震, (5): 16--17.

Diao G L, Yu X C. 1982. Change of the contradiction ratio of composite fault-plane solutions before Haituoshan earthquake[J].Earthquake, (5): 16--17 (in Chinese).

刁桂苓, 于利民, 李钦祖. 1994. 强震前后震源区应力场变化一例[J]. 地震学报, 16(1): 64--69.

Diao G L, Yu L M, Li Q Z. 1994. An example of stress field in source area before and after strong earthquake[J].ActaSeismologicaSinica, 16(1): 64--69 (in Chinese).

荣代潞. 2014. 研究中强地震前中小地震震源机制变化的一种方法[J]. 地震工程学报, 36(2): 286--291.

Rong D L. 2014. Analyzing changes of focal mechanism of small-moderate earthquakes before a moderate-strong earthquake[J].ChinaEarthquakeEngineeringJournal, 36(2): 286--291 (in Chinese).

万永革. 2008. 美国Landers地震和Hector Mine地震前震源机制与主震机制一致现象的研究[J]. 中国地震, 24(3): 216--225.

Wan Y G. 2008. Study on consistency of focal mechanism of mainshock and that of preshocks in Landers and Hector Mine earthquake in United States[J].EarthquakeResearchinChina, 24(3): 216--225 (in Chinese).

王俊国, 刁桂苓. 2005. 千岛岛弧大震前哈佛大学矩心矩张量(CMT)解一致性的预测意义[J]. 地震学报, 27(2): 178--183.

Wang J G, Diao G L. 2005. Consistent CMT solutions from Harvard University before the great earthquakes in Kurile Islands and its significance for earthquake prediction[J].ActaSeismologicaSinica, 27(2): 178--183 (in Chinese).

Freed A M, Ali S T, Bürgmann R. 2007. Evolution of stress in southern California for the past 200 years from coseismic, postseismic and interseismic stress changes[J].GeophysJInt, 169(3): 1164--1179.

Global CMT. 2012. Global CMT catalog search[EB/OL]. [2015-05-01]. http:∥www.globalcmt.org/CMTsearch.html.

Hardebeck J L, Hauksson E. 2001. Crustal stress field in southern California and its implications for fault mechanics[J].JGeophysRes, 106(B10): 21859--21882.

Kagan Y Y. 2007. Simplified algorithms for calculating double-couple rotation[J].GeophysJInt, 171(1): 411--418.

Wan Y G, Sheng S Z. 2009. Seismological evidence for the convergence of crustal stress orientation before large earthquakes[J].EarthquakeScience, 22(6): 623--629.

Yamakawa N. 1971. Stress field in focal regions[J].JPhysEarth, 19(4): 347--355.

Yang W Z, Hauksson E, Shearer P M. 2012. Computing a large refined catalog of focal mechanisms for southern California (1981—2010): Temporal stability of the style of faulting[J].BullSeismolSocAm, 102(3): 1179--1194.

Zöller G, Hainzl S, Kurths J. 2001. Observation of growing correlation length as an indicator for critical point behavior prior to large earthquakes[J].JGeophysRes, 106(B2): 2167--2175.

Consistency of seismogenic stress field of preshocks to the tectonic stress field before eight earthquakes (MW≥6.0) in southern California of United States from 1981 to 2011

1)EarthquakeAdministrationofInnerMongoliaAutonomousRegion,Hohhot010010,China2)LanzhouInstituteofSeismology,ChinaEarthquakeAdministration,Lanzhou730000，China

This paper defines an index called “concentration ratio ofPaxis distribution” used for analyzing the variation of focal mechanisms of small earthquakes before moderate-strong earthquakes. And then based on the focal mechanism solutions of earthquakes in southern California in the period of 1981—2011, this paper investigates the seismogenic stress field of small events concentrating on the local tectonic stress field before eight main shocks (MW≥6.0) in the southern California. The results show a phenomenon that the “concentration ratio ofPaxis distribution” has a minimum was observed before seven earthquakes, that is, the seismogenic stress field of small events concentrates on the local tectonic stress field. It provides a method for the risk prediction of moderate-strong earthquakes.

concentration ratio ofPaxis distribution; focal mechanism solution; southern California of United States; seismogenic stress field

10.11939/jass.2015.06.006.

中国地震局地震科技星火计划项目(XH15010Y)和中国地震局老专家科研基金(201329)联合资助.

2015-05-23收到初稿， 2015-07-13决定采用修改稿.

e-mail: rongdl@gssb.gov.cn

10.11939/jass.2015.06.006

P315.72+7

A

韩晓明, 荣代潞. 2015. 美国南加州地区1981—2011年MW≥6.0地震前发震应力场与构造应力场趋于一致现象研究. 地震学报, 37(6): 948--958.

Han X M， Rong D L. 2015. Consistency of seismogenic stress field of preshocks to the tectonic stress field before eight earthquakes (MW≥6.0) in southern California of United States from 1981 to 2011.ActaSeismologicaSinica, 37(6): 948--958. doi:10.11939/jass.2015.06.006.