煤矿突发事件应急能力评价指标赋权方法

苗成林，孙丽艳，冯俊文，马 蕾

MIAO Chenglin1,SUN Liyan1,FENG Junwen2,MA Lei3

1.安徽理工大学 经济与管理学院，安徽 淮南232001

2.南京理工大学 经济管理学院，南京210094

3.南京理工大学 人文与社会科学学院，南京210094

1.School of Economics and Management,Anhui University of Science and Technology,Huainan,Anhui 232001,China

2.School of Economics and Management,Nanjing University of Science and Technology,Nanjing 210094,China

3 School of Humanities and Social Sciences,Nanjing University of Science and Technology,Nanjing 210094,China

1 引言

相对其他企业而言，煤矿企业本身是一个容易发生突发事件的行业，突发事件的影响范围比较大、造成的损失较为严重[1]，而且煤矿企业有复杂的生产系统、多个生产环节、复杂多变的地质环境条件、恶劣的生产环境条件等特点[2]，这些迫切需要煤矿企业提升应对突发事件的应急能力水平，只有如此方可在面临突发事件时能够采取有效、及时的应对措施[3]。

煤矿企业应急系统的逐步完善，应急管理的迅速发展，煤矿企业应急能力也随之产生[4]。在应对突发事件时，煤矿企业尽可能降低突发事件造成的破坏程度和损失，并在事后能够及时恢复正常生产的能力，称为煤矿企业应急能力[5]。虽然煤矿企业突发事件爆发的特点是突发性、不确定性，但应急能力要贯穿于事前、事中、事后三个阶段的每一个环节。煤矿企业应急能力的目的就是预防、控制及消除突发事件，因此，应急能力的提高能够有效地降低突发事件造成的财产损失、人员伤害以及破坏环境的程度[6]。

国内外学者及相关企业管理者对企业突发事件的应急管理研究和应急能力评价等进行了相关研究。评价煤矿企业应急能力的状况及水平[7-8]，发现缺陷与不足，采取或制定应对措施，加强应急能力系统的建设和规划，提升企业应急能力的水平，从而实现在事前能够降低突发事件的发生率、在事中能够有效地控制事件影响的恶化、在事后尽可能降低损失和尽快恢复正常生产的目的[9]。

在煤矿企业应急能力评价过程中，评价指标之间的平衡状态对评价最终的结果有很大的影响作用[10]。它们的平衡状态是根据它们的相对重要程度计算出来的，并以“权重”的方式表现出来。从行为的角度来看，影响确定评价指标权重的因素包括：指标理想值和实际值之间的差异、指标之间的关联度、输入激活因素的频率、评价者的个性及社会经济属性、权重的内在价值、指标之间的相互作用等。传统的赋权方法，如AHP 法、特征向量法、最小二乘法、熵值法、效用函数法，只考虑与其他指标之间的相互作用而忽略其他的影响因素[11]。

一般情况下，最传统的赋权方法是静态分析，其结果仅仅反映了评价者当时的直觉或感觉[12-14]。事实上，指标权重在不同情况下是变化的，包括：输入信息、时间、学习过程和环境等。因此，确立评价指标的绝对权重是不容易的。另外，传统的赋权方法都有一个共同的假设，就是存在偏好结构，但问题是如何得到。因此，问题就产生了：如果决策者的偏好不稳定，那么赋权方法是有效的吗[15]?就如同食物对一个饥饿的人的重要性与对一个正常的人是一样的吗?答案肯定是不。从习惯领域的角度来看，权重来源于决策者的习惯领域。

本文综合考虑上述的影响因素，运用习惯领域理论[16-19]研究评价指标的赋权问题。为了清晰描述在评价过程中权重的变化，根据指标之间的关联度建立了模糊有向图。根据指标的连通网络结构图，采用习惯领域提出了新的指标赋权模型，将评价作为从理想状态到实际状态的动态调整过程，以便根据不同的情况实现权重的动态变化，改进了传统的加权方法。该模型在行为机制的基础上确立权重，克服了传统加权方法的许多缺点。

2 基于习惯领域的煤矿突发事件评价指标赋权模型

2.1 模型的构建

习惯领域（HD）的概念是由游伯龙教授于1980 年首次提出的，指出人们在决策过程中经过长时间的积累形成的思想、想法逐渐习惯性地稳定下来[19]。习惯领域的主要思想是：每个人大脑所编码、储存的知识、经验、思想、方法、技巧以及各种信息等等，经过相当的时间以后，如果没有重大事件的刺激，没有全部信息的进入，这个编码和储存的总体，将处于相对稳定的状态。思想或想法（指大脑编码、储存等）一经稳定，对人、对事、对问题、对信息的反应，包括认识、理解、判断、做法等，就具有一种习惯性，也就是说具有比较固定的套套和框框或称模式、定势或图式。

基于习惯领域的煤矿突发事件应急能力评价指标赋权网络结构见图1，在该网络结构图中所有元素是相互连通的。

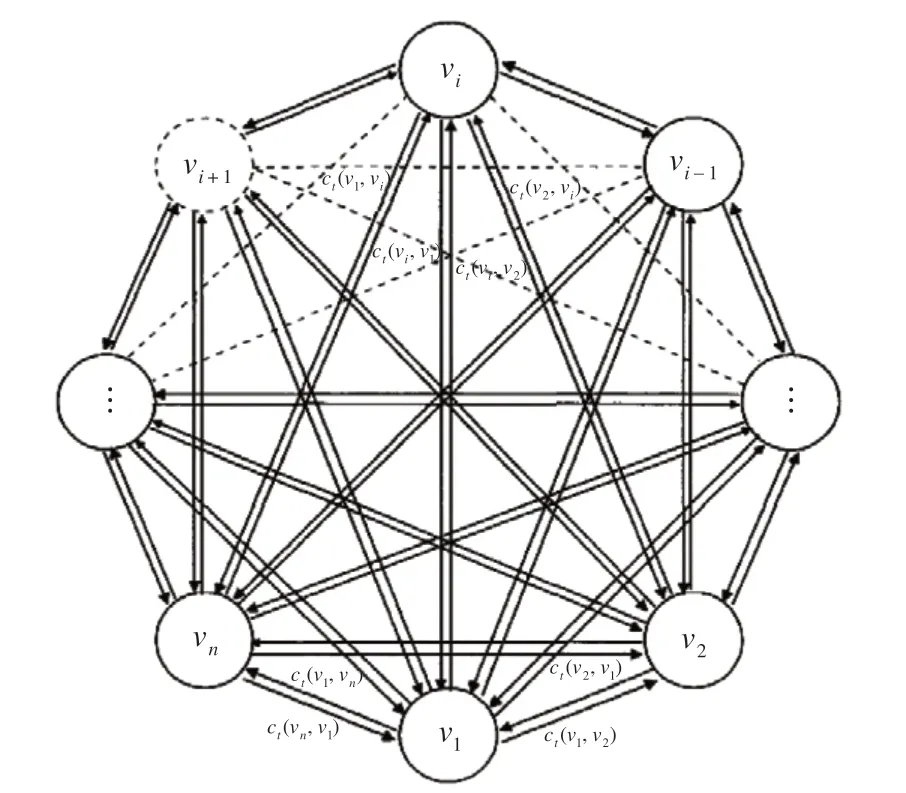
图1 基于习惯领域的评价指标赋权网络结构图

初始指标是最基本因素，且每一个指标都有与他相邻单元的路线。在外部因素的刺激下，一些指标在学习过程中被有序地激活，而其他的指标仍处于未激活状态。这些外部激活因素以路线结构图的形式被记录下来，即常表现为有向图等。这又可以反过来激活网络结构图中的其他单元，但有向图输出的信息中只有部分能够被激活。基于此，本文采用竞争学习的模式来构建煤矿突发事件应急能力评价指标赋权模型。

在竞争学习过程中，网络结构图的输出因素之间存在激烈的竞争。对每个评价指标随机赋予权重，之后给所有的输出因素一个竞争机会。这样限制了权重的大小。每个评价指标被随机赋予权重，且权重的取值在0与1 之间，即：

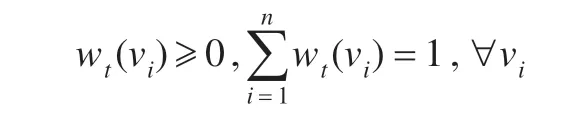
其中，wt(vi)表示输入激活信息St后指标vi（竞争层的）的权重。

内部机制在评价指标之间产生的竞争是为了准确地反映输入的激活信息，因此在某一时间内只有一个输出单元或每组只有一个单元被激活。在本文中，将在广义领域的评价指标作为竞争学习过程的胜利者。这不同于传统的“赢家通吃”观念，因为当竞争结束后，胜利者不一定只有一个。这种竞争形式被称为广义的“赢家通吃”，本文构建的赋权模型正是基于这种广义“赢家通吃”竞争学习。

令Stα表示所有“胜利”评价指标的实际域，它的ε-域为Nt(Stα，ε)。广义域的输出信号设置为1，在竞争中失败的评价指标的输出信号设置为0。输出信号也称为评价指标参数It。本文使用赢家集合及它们的邻域更新网络图的权重。然后，产生一个新的权重向量且是旧权重向量和当前输入向量的线性组合。通过网络的反复训练更新权重，权重的更新规则是：

通过控制系数和关联度函数定义每个指标vi的调整系数ηi。

对于每个vi∈Nt(Stα，ε)，vk表示vi的前一个指标，则

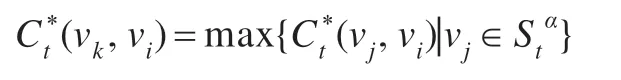
Qk表示vk的控制系数，调整系数ηi计算公式如下：

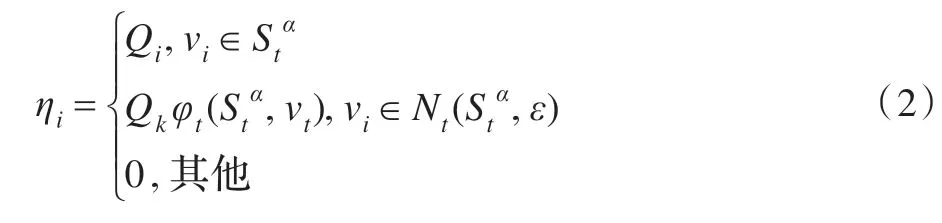
其中，映射φt:σ(HD)×HD→Ct称为习惯领域HD 子集指标的关联度函数。

假设输入激活因素有p个向量，表示所有调整系数ηi的平均值，则

调整系数的平均值，可以得到权重的变化量Δwt(vi)：

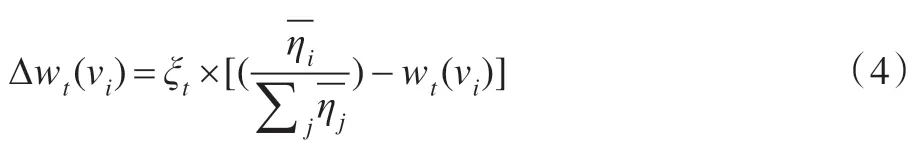
其中，ξt表示学习速率参数，它的值可自选，且ξt的值必须在0～1 之间。

引理1由式（1）～（4）所述的权重修正学习规则，在本文的研究领域中所有指标的权重之和始终等于1。

证明在时刻t，对研究的习惯领域HD 中所有指标而言，它们权重变化量之和等于0，即

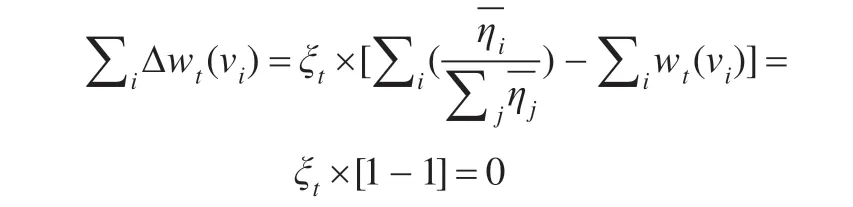
则在时刻t+1，HD 所有指标权重之和为：

∑iwt+1(vi)=∑iwt(vi)+∑iΔwt(vi)]=1+0=1

现在要讨论是平衡状态。根据引理1，在平衡状态中，评价指标的权重与控制系数和各评价指标与所在领域的关联度有关。

定理1在平衡状态中，评价指标vi的权重与控制系数和评价指标vi与其所在领域的关联度有关。而且在其他条件不变的情况下，评价指标vi的权重也是固定和稳定的。

证明设hk为激活因素Sk在网络训练出现的概率，gk(vi)表示当Sk出现时评价指标vi胜利即进入广义领域的概率。考虑以下情况：

∑kΔwt(vi)hk gk(vi)=0

也就是说，权重的平均变化值是0。将这种状态作为平衡状态。因此，根据学习规则和所有刺激因素的平均值，得到：

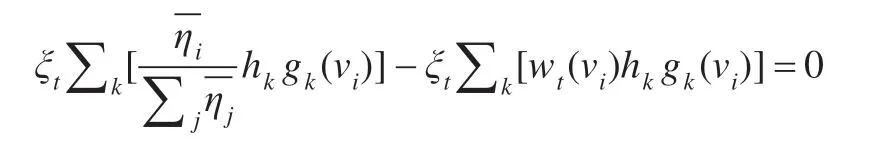
评价指标vi的平均调整系数通过控制系数和关联度函数计算得到，因此，在平衡状态中，评价指标vi的权重与控制系数和指标vi与其所在领域的关联度有关。在此情况下与控制系数与关联度对应的输入激活因素仍保持稳定状态，且平均调整系数没有发生显著的变化，评价指标权重是常数。当系统处于这种情况时，权重不会发生改变，该系统达到平衡状态。

2.2 算法

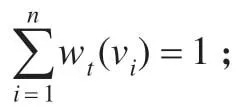
初始化连续随机变量U(0，1)，即均匀分布在区间[0，1]；

初始化ε-邻域Nt(Stα，ε)=ϕ，Stα∈2HD；

初始化ε-邻域Nt(Stα，ε)=ϕ，Stα∈2HD；

通过问卷调查得到评价指标的理想值q*、实际值q和有向图G每对(vi，vj)的初始矩阵

设置密度参数δ，0 ＜δ＜1、决策参数β，0 ≤β＜1、学习速率参数ξt和阀值参数α，0 ≤α≤1。

步骤1按下式计算有向图G的每对(vi，vj)的初始关联度：

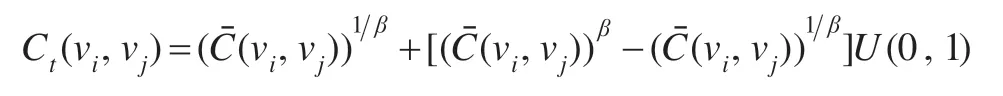
步骤2当不满足停止条件时，运行步骤3～13。

步骤3对每一个激活向量St，执行步骤4～9。

步骤4确立狭义的实际域Stα：

Stα={vi∈St∩HD|Qi≥α}，其 中

步骤5计算每一个评价指标vj∈HDStα与Stα的关联度：

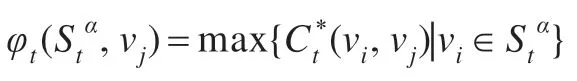
步骤6查找Stα的ε-邻域：

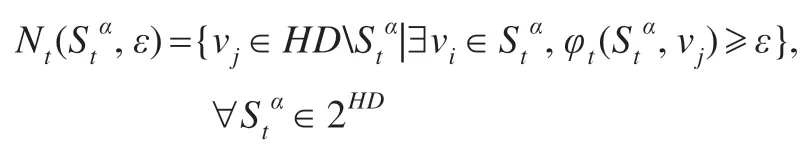
步骤7对任一vi∈Stα和vj∈Nt(Stα，ε)，Path*(vi，vj)是vi到vj的最优路径，因此φt(Stα，vj)是最大值，更新路径Path*(vi，vj)所有指标x，y 的指标参数：

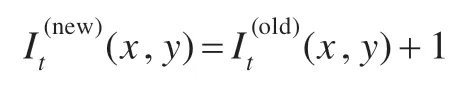
步骤8计算每个vi的调整系数ηi：

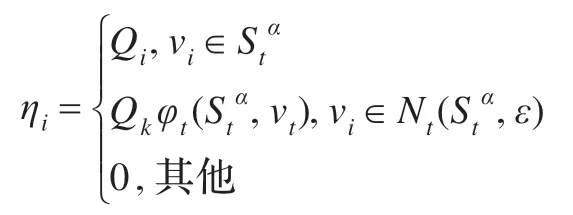
步骤9对所有vi，vj∈Stα∪Nt(Stα，ε)，更新vi到vj的关联度：

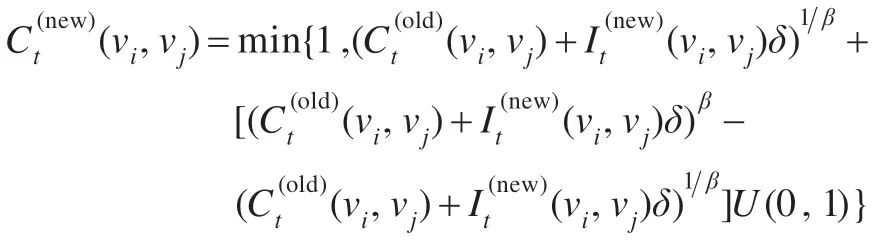
步骤10令表示所有调整系数ηi的平均值，即

步骤11计算在t+1 阶段每个评价指标vi的权重wt+1(vi)：

wt+1(vi)=wt(vi)+Δwt(vi)

步骤12更新学习速率ξt+1=0.5ξt(ξ0=0.6)。

步骤13检验停止条件：

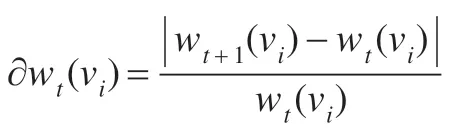
对∀i ∈[1，n]，如果maxi∂wt(vi)小于指定的公差，则停止；否则，继续。

3 仿真研究

本文对淮南市某煤矿企业进行问卷调查，以检验本文构建的评价指标赋权方法的适用性。调查该煤矿企业在煤矿突发事件前、中、后时选择方式时的决策属性以及重要等级。针对该煤矿企业的应用研究，将有助于建立更加有效的煤矿事故应对策略和处理政策。

3.1 评价指标体系的构建

煤矿突发事件应急能力是一个动态的不断变化的过程，包括事前、事中和事后三个环节的预防、监测、控制和恢复等能力。分析淮南市某煤矿企业的每个环节中应急能力的主要影响因素，根据国家煤矿安全监察局的文件并参考相关的研究成果，构建该煤矿突发事件应急能力的评价指标体系（见表1）。

表1 评价指标体系

3.2 煤矿突发事件应急能力评价指标赋权

进行问卷调查，发放160 份问卷，回收155 份有效问卷。

采用表1 的9 个评价指标和6 个激活因素进行如下实例。输入数据包括所有评价指标的关联度矩阵()、指标的公差值q*、实际值q。假设学习速率为ξ0=0.6，ξt+1=0.5ξt。

步骤0通过问卷调查得到q*和q的值。

表2 评价指标的公差值q*

表3 给出了每个评价指标的实际值。

从表4 可以看出，评价指标v3到v7的关联度最高为0.818，次之的是v3到v9的关联度为0.805，v7到v9的为0.789，v2到v7的为0.788。另外，关联度较低的是v1到v6的0.209 和v8到v4的0.225。

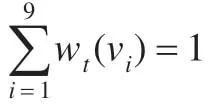
设置密度参数δ=0.000 1；设置决定参数β=0.5；设置阀值参数α=0.5。

初始化学习速率参数ξ0=0.6。假设Stα的ε-邻域的阀值为ε=0.7。

步骤1计算每对评价指标(vi，vj)的初始关联度

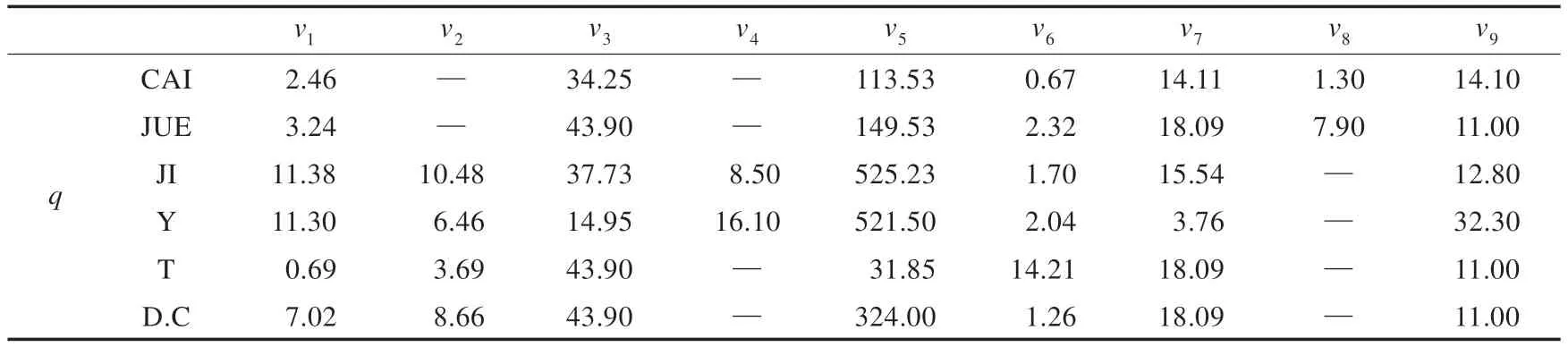
表3 评价指标的实际值q1）

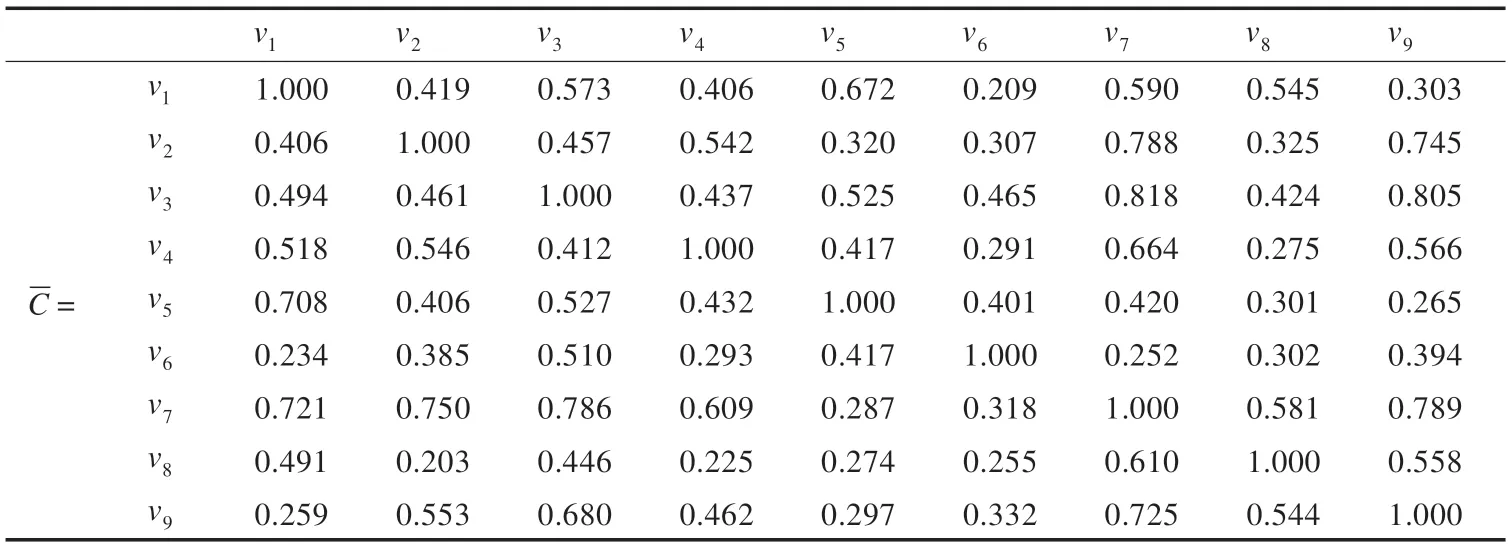
表4 总样本指标之间的关联度

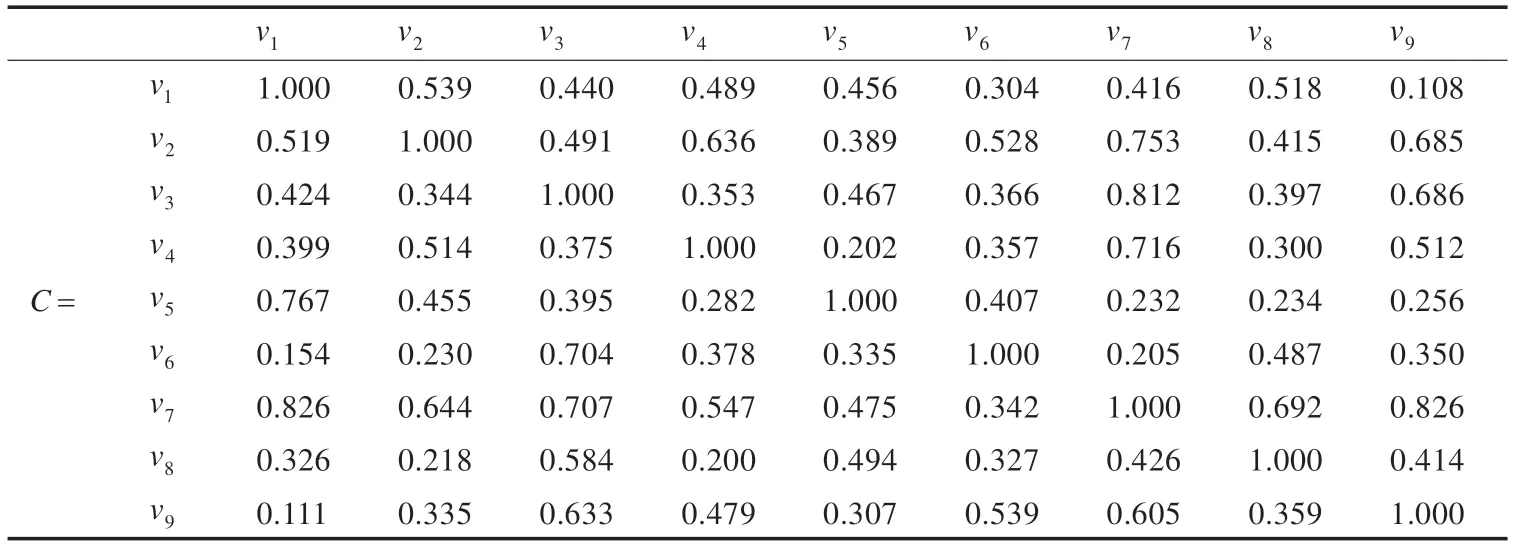
表5 每对评价指标(vi，vj)的初始关联度

步骤2由于停止条件不满足，运行步骤3～13。令t=1，进行第一次迭代。

步骤3对每一个激活向量St，执行步骤4～9。

表6 激活向量

步骤4计算每个指标vi的控制系数Qi

表7 每个指标的控制系数

确定狭义的实际域Stα：Stα={1，5，6，8}。

步骤5对每一个评价指标vj∈HDStα，计算vj与Stα的关联度。

步骤6查找Stα的ε-邻域：

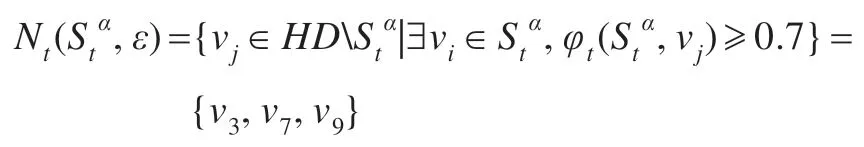
步骤7更新路径Path*(vi，vj)所有评价指标x，y的指标参数。

步骤8计算每个vi的调整系数ηi。

步骤9对vi，vj∈Stα∪Nt(Stα，ε)，更新vi到vj的关联度（直到完成一个训练过程）。

步骤10计算所有调整系数ηi的平均值。

步骤11计算在t+1 阶段每个评价指标vi的权重wt+1(vi)。

步骤12更新学习速率ξt+1=0.5ξt(ξ0=0.6)。

步骤13检验停止条件

如果maxi∂wt(vi)=0.600 4 ＞0.01，则继续。

修改学习速率的调整程序，经过7 次迭代，得到如下结果。

如果maxi∂wt(vi)=0.004 4 ＜0.01，则停止。

给出权重向量如表17。

在该煤矿突发事件应急能力的9 个评价指标中权重最高的是实际救援v6且为0.170 7；而权重最低的是应急反应v4且权重为0.075 0，这与该煤矿企业的实际情况较符合。

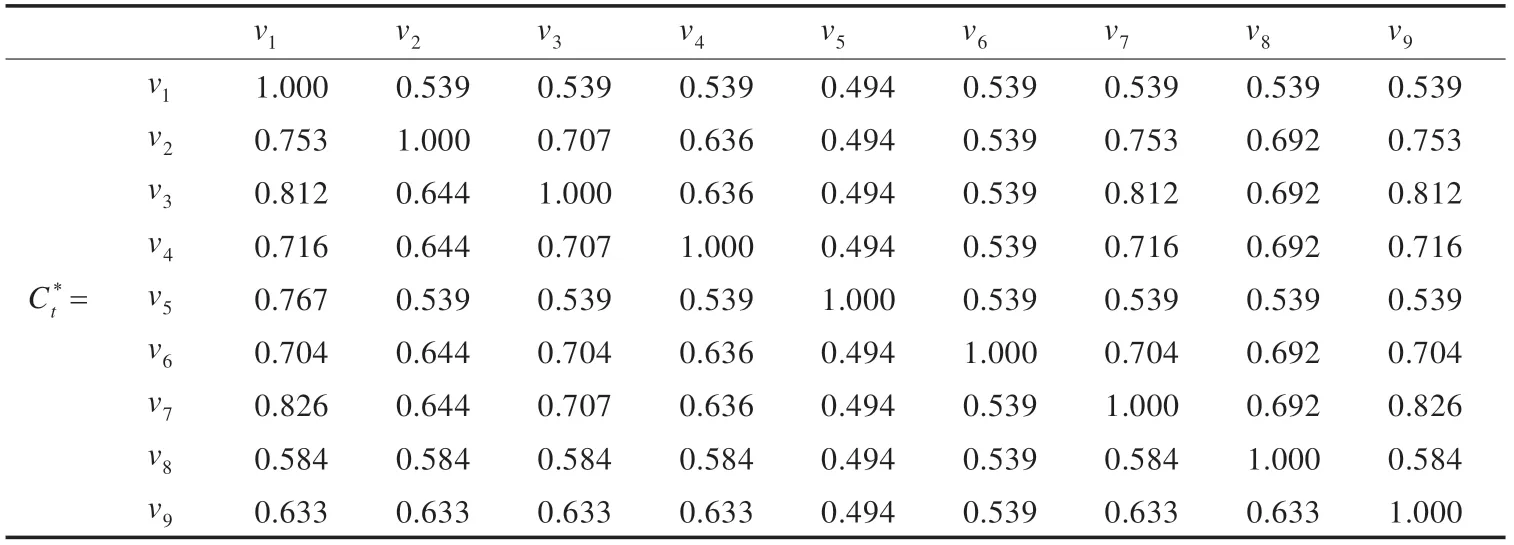
表8 vj 与Stα的关联度

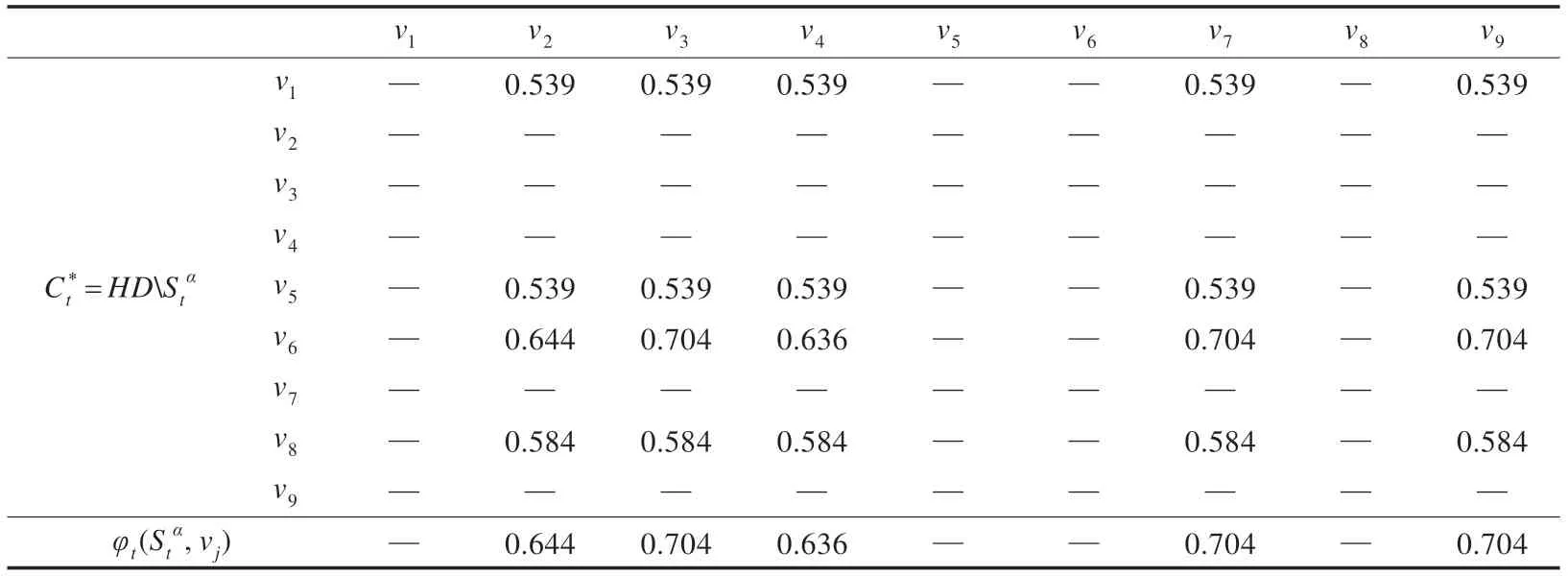
表9 vj（vj ∈HDStα）与Stα的关联度

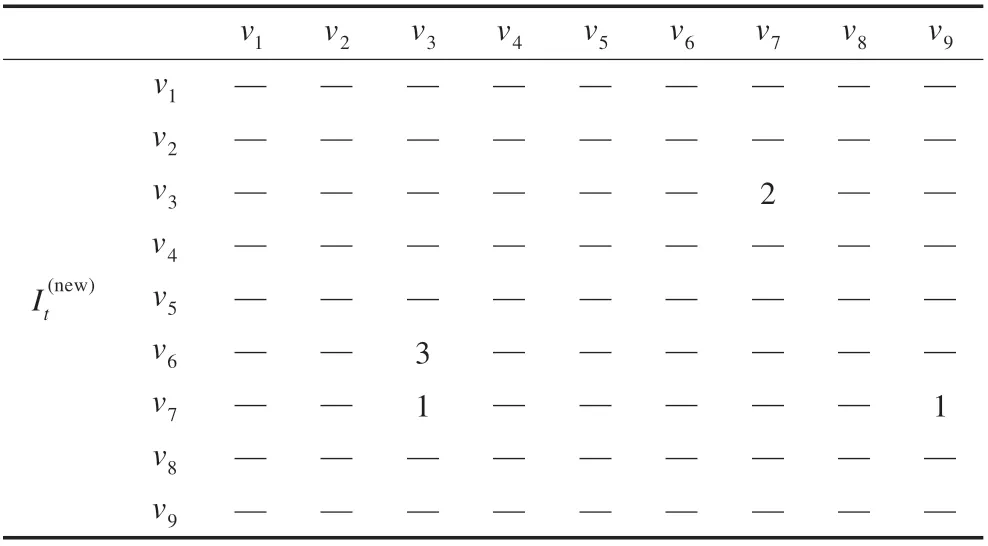
表10 Path*(vi，vj)所有评价指标x，y 的指标参数

表11 每个指标的调整系数

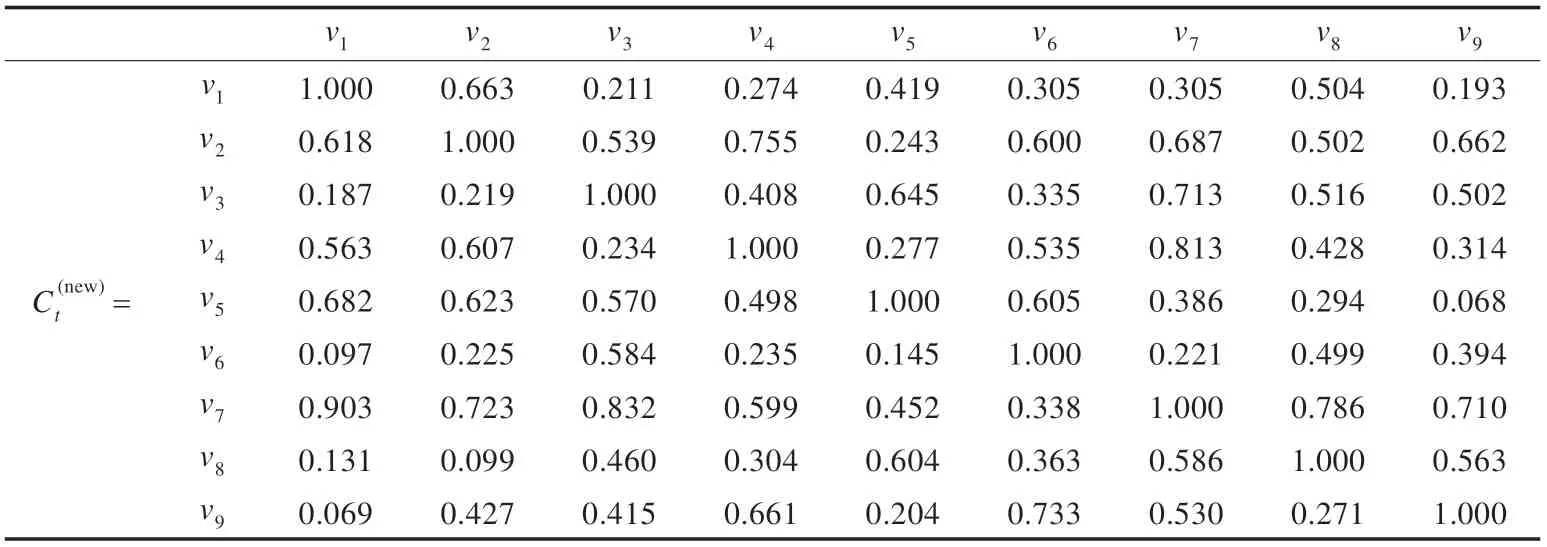
表12 更新vi 到vj 的关联度

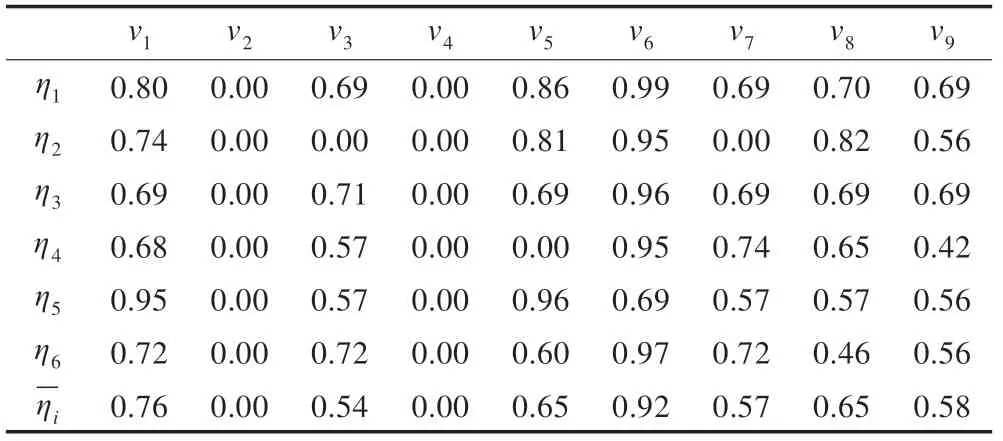
表13 调整系数ηi 的平均值

参数α，β，δ，ξ，ε的值是评价人员根据自身习惯领域的主观判断以及根据当局的需要得到的。设定参数值的规范化原则，并根据网络收敛效果测量设置的参数。在设置参数时要避免权重值发散，从而避免在网络训练过程中过度地修订参数。

3.3 与传统赋权法的比较与分析

（1）主观赋权法——AHP

表14 t+1 阶段每个指标的权重

表15 检验条件

表16 最终结果

表17 各个评价指标的权重

采用传统的主观赋权法AHP 对案例的指标体系赋予权重，得到结果如表18 所示（具体计算过程略）。

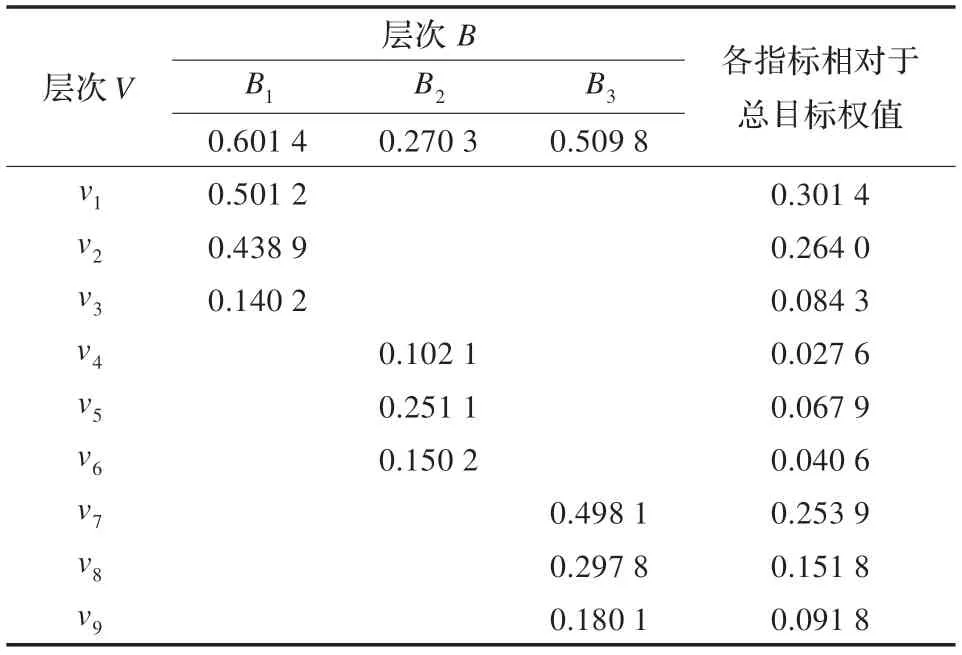
表18 AHP 赋权结果

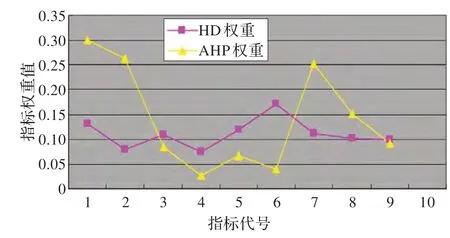
图2 HD 权重与AHP 权重的比较

图2 是本赋权方法对本文构建的评价指标体系赋予权重与运用AHP 法赋予权重之间的比较图，由图2 可以比较分析出AHP 权重的波动性比较大，而习惯领域（HD）权重则出现比较高的稳定性和比较大的同一性，说明HD 权重比传统的主观赋权法——AHP 更加准确和可靠。

（2）客观赋权法——熵值赋权法

对案例得到的指标数据标准化处理，采用下式进行归一化处理：

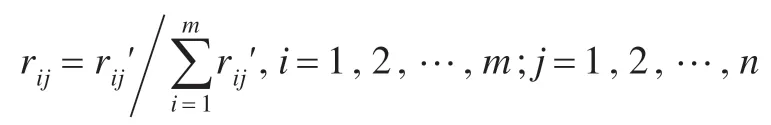
设第j个指标的熵值用ej来表示，则有

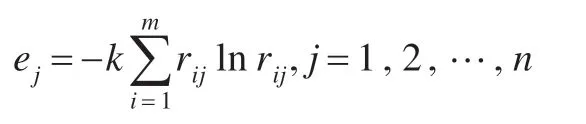
第j个指标的评价值数据的分散度dj可表示为：dj=1-ej，j=1，2，…，n。

因此，当对第j个指标没有主观偏好时，它的权重因子为：

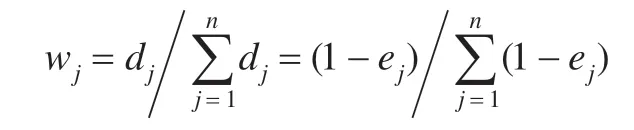
当对第j个指标有主观偏好且权重系数为λj时，它的权重因子按下式修正。

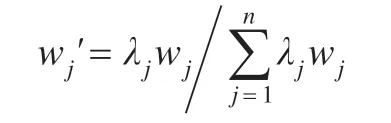
采用上述运算过程得到本案例评价指标体系的权重为：

w=(0.133 3，0.112 9，0.133 3，0.111 2，0.122 5，0.159 4，0.124 9，0.111 3，0.106 8)

图3 是本赋权方法对评价指标体系赋予的权重与熵值法赋予的权重之间的比较图，由图3 可以分析出本赋权方法得到的权重值与客观赋权法——熵值法得到的权重值几乎一致，从而说明了本赋权方法评价结果的正确性和可靠性。

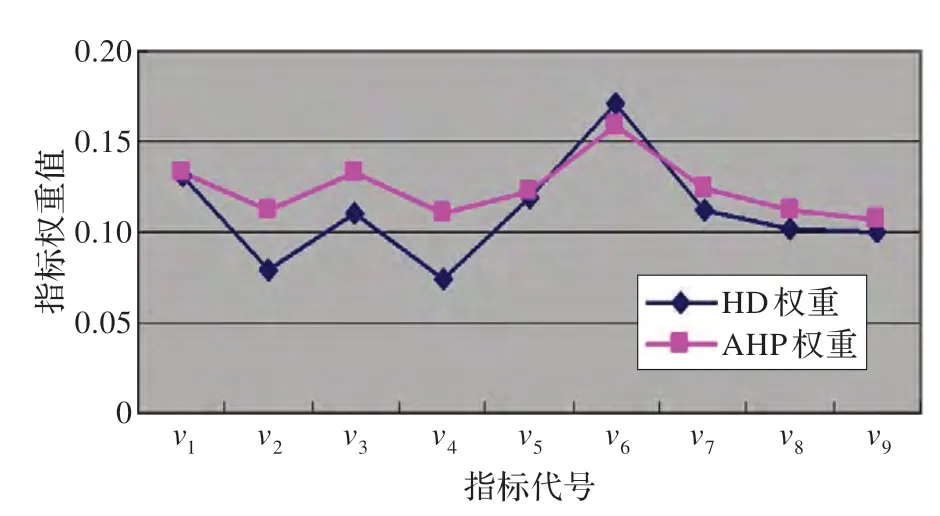
图3 HD 权重与熵值权重的比较

4 结束语

评价指标的权重是煤矿企业应急管理决策的决定性因素，本文基于行为机制模型和习惯领域理论，采用指标之间的关联度建立了煤矿突发事件应急能力评价指标赋权的网络结构图。采用关联度的思想界定了模糊有向图，并称之为关联网络图。然后，在激活反应过程中界定被激活指标的邻域，并将广泛意义上的实际领域作为广义邻域。构建的模型认为决策是从理想状态到实际状态的动态调整过程。采用习惯领域构建的煤矿突发事件应急能力评价指标赋权方法主要是从竞争学习的角度展开研究的。证明了处于平衡状态的领域的指标权重与控制系数及各指标的关联度有关。

最后，通过问卷调查法研究了淮南市某煤矿突发事件的应急能力。仿真研究的结果表明对该煤矿企业而言最重要的指标是实际救援和监测预报，而不足的是应急反应和应急物资保障。总之，与其他的传统赋权方法（AHP 法和熵值法）相比，结果表明该方法的评价结果准确和可靠。本文基于习惯领域理论建立的煤矿突发事件应急能力评价指标赋权方法将有助于煤矿企业应急管理者更准确地接近人们的思维过程，而且它的执行程序在实践中是可行的。

[1] Qi Lixia，Yang Xue.Differentiate and simulation of accident-causing mechanism in mining production[J].Safety in Coal Mines，2012（3）：116-119.

[2] 鲜林.现阶段小煤矿事故多发的原因分析及对策[J].煤矿安全，2008，39（3）：106-108.

[3] Pan Qidong.Designing research of coal mine emergency management information system based on data integration[J].Journal of Henan Polytechnic University：Natural Science，2011（5）：125-132.

[4] 祁迪.煤炭企业应急管理研究[J].山西财经大学学报：高等教育版，2009，12（4）：91-93.

[5] Gu Weili，Li Xinchun.Study on emergency capacity evaluation of coal mine enterprise[J].Coal Engineering，2011（9）：83-91.

[6] 朱桂明.石化企业应急救援能力评估研究[J].中国安全生产科学技术，2010（9）：82-87.

[7] 张江石.矿工应急处理能力评估方法研究[J].煤炭学报，2012，37（2）：290-294.

[8] 冯珍，郝晶星.煤矿企业应急救援能力评估[J].电子科技大学学报：社会科学版，2010，12（3）：53-56.

[9] 谷威丽，李新春.煤矿企业应急能力评价研究[J].煤炭工程，2011（9）：106-108.

[10] 刘业政，徐德鹏，姜元春.多属性群决策中权重自适应调整的方法[J].系统工程与电子技术，2007，29（1）：45-48.

[11] 黄德春，陆艳.创新型企业评价体系指标的测度及赋权方法[J].统计与决策，2007，22：173-175.

[12] 程平，刘伟.多属性群决策中一种基于主观偏好确定属性权重的方法[J].控制与决策，2010，25（11）：1645-1650.

[13] 宋兴光，杨德礼.基于决策者偏好及赋权法一致性的组合赋权法[J].系统工程与电子技术，2004，36（9）：1226-1290.

[14] 吕俊杰，王元卓.信息安全风险模糊群决策评估方法[J].计算机工程与应用，2010，46（12）：17-20.

[15] 刘伟，周育人.一种改进惯性权重的PSO 算法[J].计算机工程与应用，2009，45（7）：46-48.

[16] 冯俊文.组织习惯域理论[J].系统工程与电子技术，2001，6（23）：40-43.

[17] 冯俊文，王华亭，宁方伟，等.习惯领域与能力管理[M].北京：经济管理出版社，2010.

[18] 马蕾.企业组织惯域理论研究与应用[D].南京：南京理工大学，2003.

[19] Yu P L.Habitual domains[J].Operations Research，1991，39（6）：869-876.