欧拉算子系统柔性变结构控制器设计
刘云龙, 马云峰, 徐国盛,2, 王文成
(1. 潍坊学院 信息与控制工程学院, 山东 潍坊 261061; 2. 北京交通大学 电子信息工程学院, 北京 100044)
欧拉算子系统柔性变结构控制器设计
刘云龙1, 马云峰1, 徐国盛1,2, 王文成1
(1. 潍坊学院 信息与控制工程学院, 山东 潍坊 261061; 2. 北京交通大学 电子信息工程学院, 北京 100044)
针对带有不确定参数的模拟信号系统,提出了一种基于Sigmoid函数的饱和变速趋近律方法,设计了欧拉算子柔性变结构控制器。基于欧拉算子采样原理,将模拟信号系统和采样信号系统的变结构控制器设计统一到欧拉算子系统。该柔性变结构控制器在采样频率很高时,其稳定性仍与相应的模拟信号系统保持一致。给出了一个有源电力滤波器仿真实例,比较基于指数趋近律方法设计的变结构控制器,该柔性变结构控制器的抖振幅度较小,基波电流有良好的跟踪补偿。
欧拉算子; 移位算子; 变结构; 饱和变速趋近律; 柔性
0 引 言
随着现代工业自动化的发展,电子通信,化工流程等实际领域的检测与控制精度越来越高,以采样技术为核心的计算机控制(Computer Control, CC)迅速成为控制科学领域的研究热点。采样控制是按照一定的间隔时序对模拟信号进行样本采集,将其转换为相应的脉冲序列,是计算机控制实现的重要转换途径。对于模拟信号系统,利用移位算子采样时,如果频率过高,系统状态轨线将趋近于稳定圆域的边界,使得采样系统并不趋近于原来的模拟信号系统,可能引起环形振荡,甚至造成系统失稳,降低控制器使用寿命[1]。欧拉算子是一种增量差分算子,又称为Delta算子,能够统一描述模拟信号系统和采样信号系统[2]。利用欧拉算子采样的控制系统能够较好处理数字信号,即使采样频率非常高,其稳定性仍与原来的模拟信号保持一致,在有源电力滤波器(active power filter, APF)[3]、热能快速转化器[4]等实际系统中具有广泛的应用。
对于不确定系统,研究系统可靠性诊断与控制策略优化非常重要,如最优控制[5]、模糊控制[6]。变结构控制也是一种有效的处理不确定系统的控制策略,在一定的匹配条件下,当系统状态轨线到达切换面后,总会处于滑动模态,具有很强的完全自适应性,又称滑模控制[7]。趋近律方法是变结构控制系统设计中采用主动设计思想的算法,实用可靠。针对采样控制系统,文献[8]提出了采用指数趋近律,所设计的变结构控制器调节时间短,响应速度快,但产生了抖振,影响了它的推广应用。文献[9]给出了能够趋近平衡状态的变速趋近律。人工神经网络技术中的sigmoid函数,是典型的具有光滑饱和性的柔性函数。文献[10]利用sigmoid函数改进了采样指数趋近律。文献[11]基于sigmoid函数设计了一种软变结构水下机器人。文献[12]基于S型函数构造了受限系统的软变结构控制器,较好地削弱了系统抖振。文献[13]给出了欧拉算子变结构控制系统实现稳定切换面的充分条件和控制器设计。文献[14]设计了基于指数趋近律方法的欧拉算子变结构控制系统。文献[15]基于欧拉算子构造了不确定鲁棒变结构控制器。对于欧拉算子系统,基于柔性变结构控制策略的研究成果很少。
针对带有不确定参数的模拟信号系统,基于移位算子采样的变结构控制系统容易出现抖振的问题,利用sigmoid函数,提出一种饱和变速趋近律,基于欧拉算子采样,设计欧拉算子柔性变结构控制器。该控制器既有效地削弱了系统抖振,又能在有限时间内趋近切换面,最终稳定于平衡状态,具有良好的动态性能。
1 系统描述
欧拉算子的数学表达式为
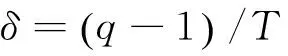
(1)
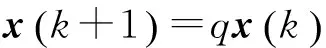
考虑如下模拟信号系统:

(2)

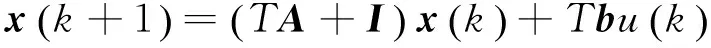
(3)
其中,I为单位矩阵。利用欧拉算子采样,得如下系统:
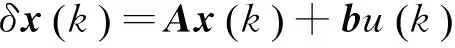
(4)
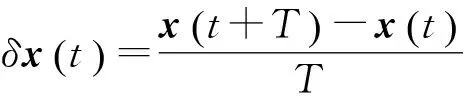
实际问题中,系统往往存在着未建模动力学等不确定因素,给出如下带有不确定参数的欧拉算子系统:
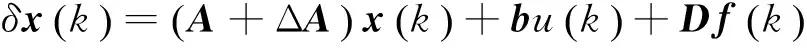
(5)

式(5)对应的标称系统为
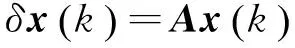
(6)
2 欧拉算子饱和变速趋近律
文献[8]给出基于移位算子采样指数趋近律:

(7)
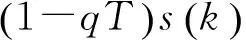
文献[9]给出了变速趋近律:
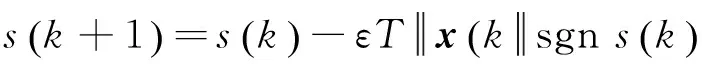
(8)



(9)
式(9)能够使得系统最终趋近于平衡状态,但该方法的缺点是需要已知精确的数学模型,不具有鲁棒性[16]。
人工神经网络技术中的sigmoid函数是一类连续、可导、饱和有界的激励函数,其数学表达式为
(10)

(11)
由于指数式(7)和变速式(8)都有难以克服的问题,同时,组合趋近律也不易准确实施切换,利用sigmoid函数,给出了一种欧拉算子饱和变速趋近律:

(12)
当系统在趋近过程阶段,此时离平衡状态较远,有
因此,饱和变速趋近律(12)可化简为

(13)
这表明在趋近过程阶段内,系统能够在有限时间内快速到达切换面。利用线性矩阵不等式技术,由引理1知,据文献[13],可以求取切换函数的系数矩阵。
当系统在滑动模态过程,此时一般离平衡状态较近,根据等价无穷小量理论,由L'Hospital法则,有:
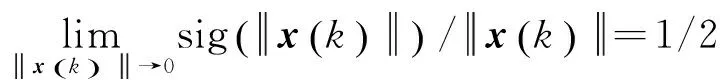


(14)
3 欧拉算子柔性变结构控制器设计
欧拉算子系统柔性变结构控制器设计分为两个过程:首先选取线性形式或积分型等非线性形式的切换函数,目的是保证系统状态轨线进入切换区域后,平稳趋近到滑动模态区域;其次,构造欧拉算子柔性变结构控制律,使得从任意初态出发的系统状态轨线快速到达切换面,并最终稳定于平衡状态或在平衡状态附近形成较小的抖振。
这里选取线性切换函数:
(15)
其中:c∈Rn满足Hurwitz条件。构造切换面为
(16)
构造切换带为
(17)
其中:2ω为切换带的带宽。
考虑不确定欧拉算子系统式(5),假定内部参数摄动和外在扰动满足如下匹配条件:
ΔA=baT,D=bdT
(18)
其中,a∈Rn,d∈Rl。
假定选取的向量c使得cTb≠0,采用饱和变速趋近律式(12),得欧拉算子柔性变结构控制律为
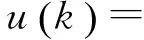
(19)
对于柔性变结构控制律式(19),其中含有不确定参数,无法直接物理实现,其完全自适应性并不能保证。要使柔性变结构控制律式(19)能够直接实施,需要限制系统不确定因素的变化范围在有界区域,将该控制律的不确定因素用其上、下确界代替。这样,该控制律就成为可直接实现的控制律。
考虑不确定参数是有界的,无妨假设
(20)
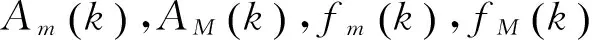
可得:
① 优化调节时间和响应速度的切换结构

② 削弱外在干扰因素影响的切换结构
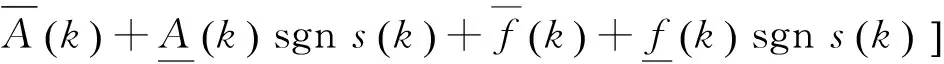
于是,得到可直接实现的欧拉算子柔性变结构控制律:

(21)
将不确定参数的匹配条件式(18)、有界条件式(20)和柔性变结构控制律式(21)代入不确定欧拉算子系统式(5)中,有:
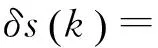
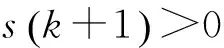
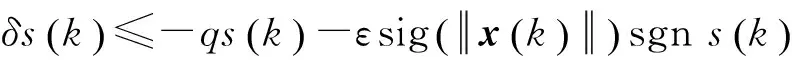
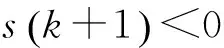
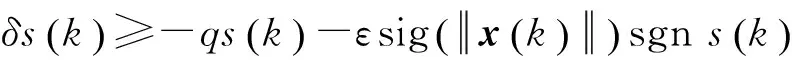
这表明不确定欧拉算子系统式(5),在不确定参数满足有界和匹配条件的前提下,存在着柔性变结构控制律式(21),使得系统在滑动模态阶段具有完全自适应性。

4 实例仿真
本节给出一个实例说明柔性变结构控制器设计的可行性。考虑某APF控制器,相关参数如下:电源电压为380 V,等效电源电阻为0.1 Ω,等效电源电感为2 mH,连接电感为1.5 mH,高通滤波器电容为30 μF,滤波电阻为1 Ω,非线性负载为不可控阻感负载整流器,给出的欧拉算子系统为
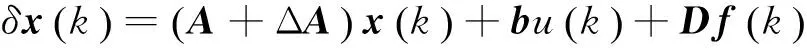
相关参数如下:
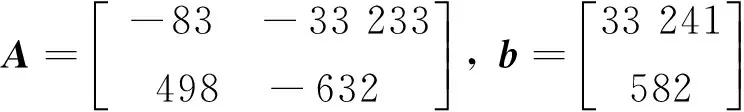
为进行仿真分析,负载整流器参数为
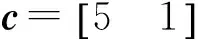
利用移位算子采样,给出采样信号系统为

相关参数如下:

基于指数趋近律(7)设计的APF变结构控制器的基波电流波形如图2所示。

图1 基于趋近律(12)设计的APF基波电流波形
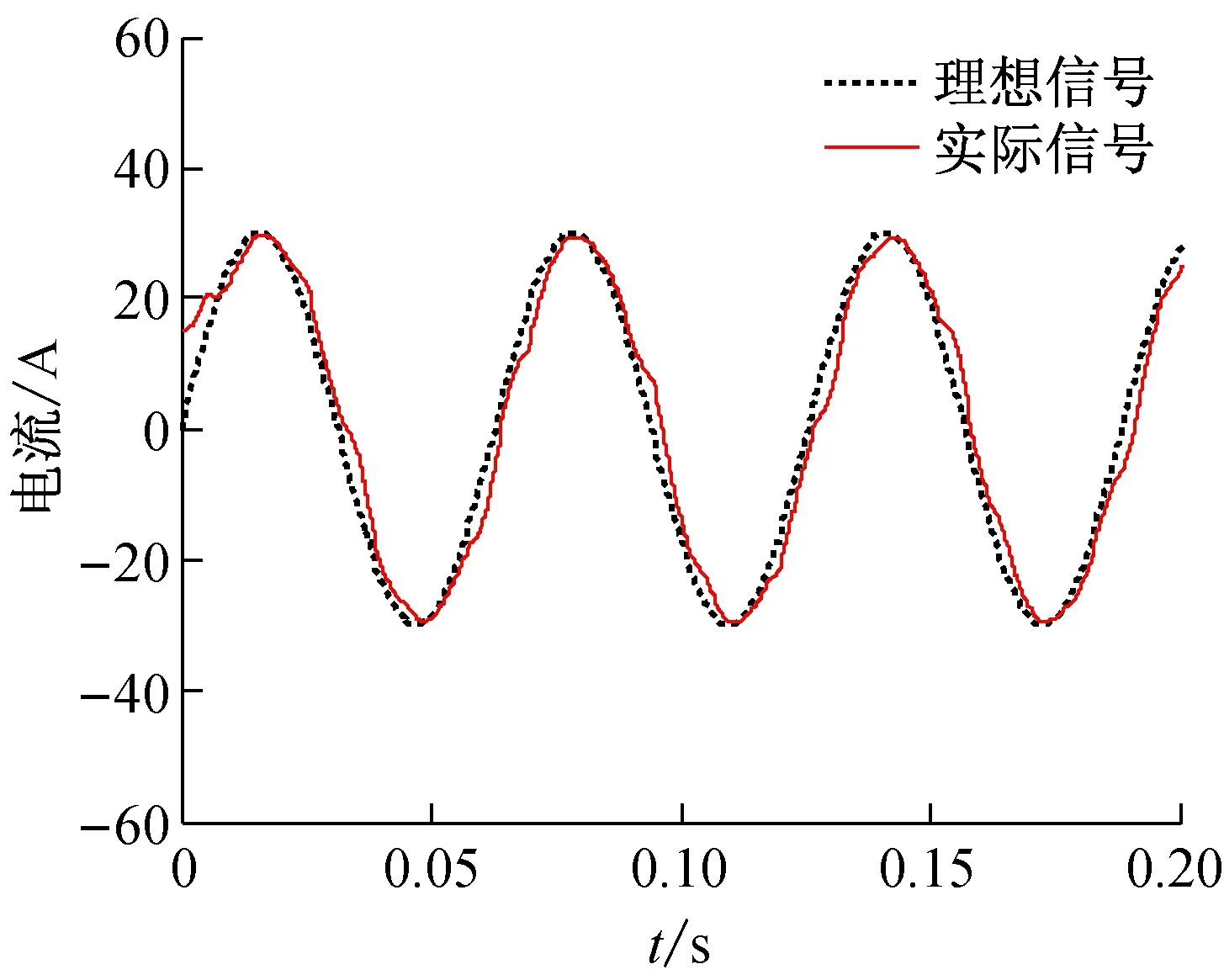
图2 基于趋近律(7)设计的APF基波电流波形
图3和图4分别为基于饱和变速趋近律式(12)设计的APF柔性变结构控制器和基于指数趋近律式(7)设计的APF变结构控制器的输入变化曲线。
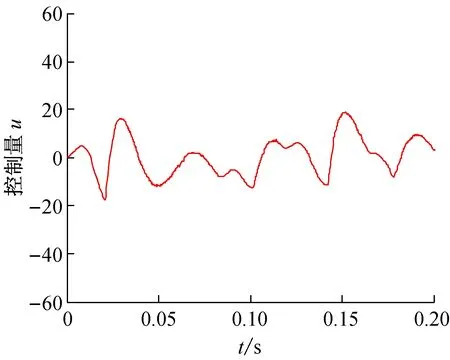
图3 基于趋近律(12)设计的APF柔性变结构 控制器的输入曲线
对比图1、图2的基波电流补偿效果,基于欧拉算子采样,利用饱和变速趋近律式(12)设计的APF柔性变结构控制器补偿效果优于利用传统移位算子采样设计的APF变结构控制器。若进一步增大采样频率,传统移位算子采样方法设计的变结构控制器抖振幅度增大,使得控制系统变得不稳定,而基于欧拉算子采样设计的柔性变结构控制器仍然具有良好的稳态性能。
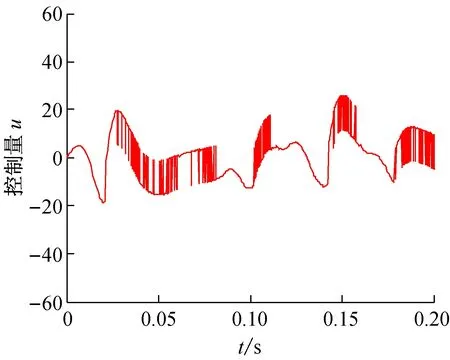
图4 基于趋近律(7)设计的APF变结构控制器的输入曲线
5 结 语
将模拟信号系统和采样信号系统的变结构控制器设计统一到欧拉算子系统,消除了移位算子采样过程易产生的病态问题。基于饱和变速趋近律方法,设计了不确定欧拉算子系统的柔性变结构控制器,具有良好的动态性能和稳态性能。另外,具有时间滞后的欧拉算子柔性变结构控制器设计有待于进一步研究。
[1] Goodwin G C, Middleton R H, Poor H V. High-speed digital signal processing and control [J]. Proceedings of the IEEE, 1992, 80(2): 240-259.
[2] 李惠光, 武 波, 李国友, 等. Delta算子控制及其鲁棒控制理论基础[M]. 北京: 国防工业出版社, 2005.
[3] 齐 虹, 林瑞全. 基于Delta算子的并联型有源电力滤波器H∞控制器设计 [J]. 电力自动化设备, 2011, 31(1): 37-40.
[4] Won W, Lee K S. Identification of a multivariable Delta operator stochastic state-space model with distributed time delays: application to a rapid thermal processor [J]. Computers & Chemical Engineering, 2012, 40(11): 223-230.
[5] 王 青, 张颖昕. 基于遗传算法的倒立摆实验系统最优控制器 [J]. 实验室研究与探索, 2010, 29(5): 22-25.
[6] 付敏玲, 胡天友, 杨 攀, 等. 基于模糊控制的光伏能量补偿研究与设计 [J]. 实验室研究与探索, 2013,32(12): 27-30.
[7] 刘云龙. 变结构控制策略及在广义系统和δ算子系统中设计研究 [D]. 青岛: 中国海洋大学, 2012.
[8] Gao W, Wang Y, Homaifa A. Discrete-time variable structure control systems [J]. IEEE Transactions on Industrial Electronics, 1995, 42(2): 117-122.
[9] 姚琼荟, 宋立忠, 温 洪. 离散变结构控制系统的比例-等速-变速控制 [J]. 控制与决策, 2000, 15(3): 329-332.
[10] 高存臣, 刘云龙, 李云艳. 不确定离散变结构控制系统的趋近律方法 [J]. 控制理论与应用, 2009, 26(7): 781-785.
[11] 刘云龙, 高存臣, 任启峰, 等. 水下机器人基于sigmoid函数的软变结构控制 [J]. 电机与控制学报, 2012, 16(2): 90-95.
[12] Liu Y, Gu S, Kao Y,etal. Soft variable structure controller design for constrained systems based on S-class functions [J]. Neural Computing and Applications, doi: 10.1007/s00521-014- 1748-0, 2014,
[13] 张彩虹, 刘云龙, 高存臣, 等. Delta算子不确定系统的滑模变结构控制 [J]. 控制与决策, 2012, 27(2): 237-242.
[14] 刘云龙, 韩星海, 唐述宏. 基于趋近律方法的 Delta 算子滑模变结构控制系统 [J]. 计算机应用, 2013, 33(8): 2397-2400.
[15] Xia Y, Fu M, Yang H,etal. Robustness sliding mode control for uncertain time-delay systems based on delta operator [J]. IEEE Transactions on Industrial Electronics, 2009, 56(9): 3646-3655.
[16] 刘金琨. 滑模变结构控制MATLAB仿真 [M].2版. 北京: 清华大学出版社, 2012.
加快解决经济社会发展对高质量多样化人才需要与教育培养能力不足的矛盾、人民群众期盼良好教育与资源相对短缺的矛盾、增强教育活力与体制机制约束的矛盾,为教育事业持续健康发展提供强大动力。
——摘自《国家中长期教育改革和发展规划纲要》
Design of Flexible Variable Structure Controller for Euler Operator System
LIUYun-long1,MAYun-feng1,XUGuo-sheng1,2,WANGWen-cheng1
(1. College of Information and Control Engineering, Weifang University, Weifang 261061, China;2. School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China)
Aiming at Euler operator system with uncertain parameters, a novel reaching law method, named saturated variable rate reaching law, is proposed based on the sigmoid function, and a flexible variable structure controller is designed based on saturated variable rate reaching law in this paper. By the designed variable structure controller, the analog signal system and sampling signal system can be unified into the Euler operator system based on the principle of Euler operator sampling. When sampling frequency is very high, the flexible variable structure controller can make the stability of the control system be closed to the original analog signal system. A simulation example of active power filter is given to demonstrate the application of the controller. Compared to variable structure controller based on exponential reaching law, the proposed flexible variable structure controller can reduce the chattering, and has a good compensation of fundamental current.
Euler operator; shift operator; variable structure; saturated variable rate reaching law; flexible
2014-10-31
国家自然科学基金资助项目(61403283);山东省高等学校科技计划项目(J13LN81);潍坊市科学技术发展计划项目(2014GX022);潍坊学院博士科研基金项目(2013BS10)
刘云龙(1982-),男,山东日照人,博士,讲师,主要研究方向为滑模控制,离散控制,电机控制。
Tel.: 13562650201; E-mail: fhylren@163.com
TP 273
A
1006-7167(2015)05-0093-04

