Measurement of associations between mobile calls and mobile-internet surfing①

Song Zhu (宋 竹)

(School of Computer Science & Engineering, University of Electronic Science and Technology of China, Chengdu 610054, P.R.China)



Measurement of associations between mobile calls and mobile-internet surfing①

Song Zhu (宋 竹)②

(School of Computer Science & Engineering, University of Electronic Science and Technology of China, Chengdu 610054, P.R.China)

Measuring mobile calls data is an increasingly import issue, which will benefit to the understanding of the behavior of mobile users and assist telecom operators to optimize their business strategies. The existing researches on cell phone data measurement only focus on mobile calls or on mobile-internet surfing and little researches focus on the interactions of behaviors between them. In this paper, some basic factors of the association between mobile calls and mobile-internet surfing are measured. Then first their distributions are compared and the preference of users is quantified. After that experiments on the curve fitting of both the whole and parts of these distributions are done. Through the comparison of the correlation coefficients and Fourier fitting parameters, different behaviors is found between workdays and weekends, as well as Saturdays and Sundays in mobile-call distributions. Besides, the results of our observation show that the mobile-internet traffic does not always monotone increase with the increase of online time, significant changes are observed after 8 hours of mobile-internet surfing.

measurement, distribution, mobile calls, mobile-internet surfing, fitting

0 Introduction

Now modern smart phones provide a variety of communication modes, such as short message service, multimedia message service, cell phone conversation, video chat, email and online instant messaging. Recently mobile-internet also becomes a hot research topic since it plays an increasingly important role in mobile services.

Existing studies focus on either mobile calls or mobile-internet surfing. Recent studies on mobile calls focus on the distribution of interval duration[1], time based patterns[2], temporal factors on mobility patterns[3]and the weighted undirected mobile network[4]. In particular, they measure three factors including out-degree, percentage of outgoing calls, and communication diversity to quantify individual users and classify user clusters[5].

Resent studies on mobile-internet surfing include qualitative studies on statistical analysis[6], mobile-internet behaviors[7-9], quantitative studies on user groups[10-12]， time based patterns[13-15]; difference between mobile-internet surfing and web surfing[16]， categories of visited pages[17-19], and the variation of visited pages over time[20].

As far as we know, few studies comparatively analyze the distribution of mobile calls and mobile-internet surfing. This paper focuses on the characteristics and differences of these distributions and makes further study according to the associated data of mobile calls and mobile-internet using Fourier function and Polynomial function. Instead of analyzing the interval duration, it tries to find characteristics and laws between user behaviors on mobile calls and mobile-internet surfing. Here behaviors of mobile users based on two four-day datasets are studied: mobile billing data and mobile-internet billing data.

Main observations and contributions in this paper are listed as follows:

1. Four indicators are used to quantify individual users including the amount of out-going calls, the sum duration of these calls, the sum online time of mobile-internet surfing and the use amount of mobile-internet traffic. All individual user behaviors have beeen normalized and over 86% of users is more prone to using either mobile call or mobile-internet surfing. Such observation is complied with the Pareto Law;

2. It is found that typical human circadian rhythm has a great impact on the distribution curves of mobile calls, and significant difference exists between workdays and weekends. Considering these distributions as signals, Fourier function, a widely used fitting method in signal processing, is adopted to fit these curves. In particular, 5-order Fourier function and Polynomial function are used to fit different parts of these curves. The fitting result gives the formal description of the difference.

3. The observation shows that the amount of mobile-internet traffic is not monotonically increasing with its online time. From a macro point of view, when the online time comes to about 2 hours per day, the use ratio of mobile-internet traffic approaches to its maximum value.

The rest of this paper is organized as follows: Section 1 presents the measurement of associated data. Section 2 introduces experiment result of our mobile call data. In Section 3 a similar method is used to measure the mobile-internet data and other relative experiments on it is done. Finally the paper is concluded with our contributions and outlines ideas we plan to explore in the future, which are both helpful for optimizing business strategies.

1 The measurement of associated data

There are two datasets analyzed in this paper. One is the mobile billing data and the other is the mobile-internet billing data. They are all the anonymous cell phone users’ real billing data provided by a wireless provider in a city of China. Such data cover 1012 base stations of the whole city, contain all of the calling records from December 1 to December 4, 2011.The user group of the operator in this city is above 1.5 million and the operator is not the only biggest one in this city.

For each entry of mobile billing record, we have the information of caller number, callee number, call

starting time, call length and base station ID. For each entry of mobile-internet billing record, we have the information of user number, online time, the time of access and disconnect, amount of traffic received and sent, base station ID. Note that we only take into account local calls without special numbers. The entries of records that are not completed, interrupted or contain non-local base station ID are discarded. Interrupted records indicate two calls share a same period for a given individual user.

1.1 Features of associated data

There are 1962989 records and 400684 individual users in our mobile billing data. While in mobile-internet billing data there are 3618970 records and 295091 individual users. There exist users either having no mobile call records or mobile-internet surfing records.

The user distribution with the frequency of calls is shown in Fig.1. The amount of the users is inversely proportional to the number of out calls.

(X-axis is the number of calls for an individual;

In the data, each call or internet access is saved in different entries. Some features of the mobile-internet data and mobile call data are listed. The features of them are shown respectively in Table 1 and Table 2:

Table 1 Features of mobile-call data

Table 2 Features of mobile-internet data

95% cumulative percentage of the online time distribution of mobile calls and mobile-internet surfing is counted respectively shown in Fig.2. It can be clearly found out that the frequency distributions of mobile calls and mobile-internet surfing are different in patterns. Fig.2(b) exhibits excellent Poisson behaviors with the mode of the online time appearing at 15s. On the other hand, the frequency distribution in Fig.2(a) is not regular. The mode appears at 46s is where the data start to record and there exist crests ranging from 650 to 700 seconds.

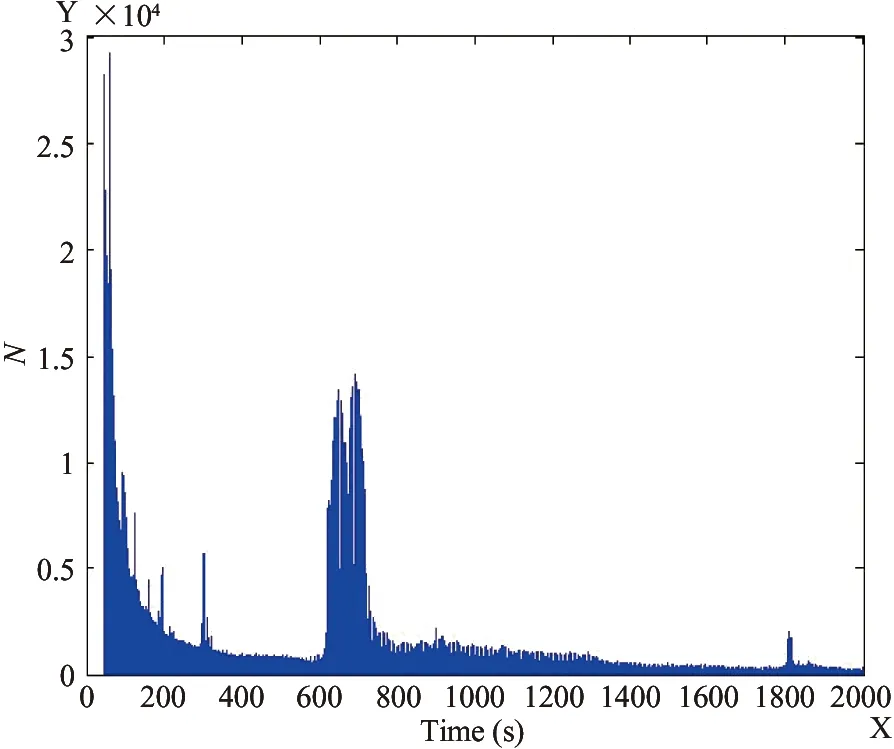
(a) mobile-internet surfing

(b) mobile calls

1.2 The preference of users

To discover the use model of both the mobile call and mobile-internet surfing, Piis defined as the proportion of the usage of mobile-internet surfing to normalize the preference of individual user. Let xiand yirespectively be the sum online time that user i spends on mobile calls and mobile-internet surfing. The formula is shown as

(1)

(X-axis is the proportion of the preference of using mobile-internet;Y-axis is the number of users)

The proportion distribution of the preference of using mobile-internet surfing is shown in Fig.3. Table 3 lists the details of the user amount.

Table 3 The distribution of user amount and proportion

It can be seen clearly that the distribution is concentrating at both ends, which shows an extreme state that the majority of users (over 86%) are more prone to using either mobile call or mobile-internet surfing. Besides, more users prefer to use mobile call than mobile-internet surfing. Such result is complied with the Pareto Law. The result has benefit in understanding the behavior of mobile users, and it is helpful for telecom operators to optimize their business strategies.

2 The measurement of mobile calls data

Being different from other coarse-grained analysis, the scales of x-axis in our figures are up-to second. It is helpful for us to discover detailed patterns and distinguish imperceptible changes (e.g., fluctuations in a short period of time).

By observation, we can easily distinguish a pattern from the mobile-call distributions. Such pattern is similar to a law in bimodal distribution called ‘the typical human circadian rhythm’. While from fine-grained distributions a few differences are found (e.g., mobile-call distributions are diminishing from time period 0:00 to 4:00 except that in Day 1, because it is the beginning of the data and the distribution is counted cumulatively). To avoid the impact of such error, the data in time period from 0:00 to 4:00, a common inactive period of physiology, are all dismissed in following sections.

It is found that all distributions are rapidly increasing from 4:00 to 11:00 until the first and highest crest appear (Day 1 appears at 10:28; Day 2 appears at 10:53; Day 3 appears at 11:00 and Day 4 appears at 11:06). After that the amount of active users is continually decreasing till about 14:00. During the period of 14:00 to about 16:00 there exists a difference between workdays (Day 1, Day 2) and weekends (Day 3, Day 4). It can been seen the mobile-call distributions in weekends are decreasing smoothly, while the distributions in workdays are still growing. The secondary crests observed in workdays appear at about 18:00 are not that obviously in weekends (Day1 appears at 17:36; Day2 appears at 17:28; Day3 appears at 17:12 and Day4 appears at 17:05). In the period between 18:00 to 20:30, distributions decrease and distributions of weekends decrease relatively gently. After that, they all decrease rapidly from 20:30 to 0:00 the next day.

2.1 Correlation analysis of mobile-call data

A conclusion is drawn that mobile-call distributions are different in workdays and weekends by observation. To verify the result, correlation coefficient is used to evaluate the similarity of the distributions of mobile calls. The correlation coefficient R, related to the covariance C shown in Eq.(2), is a parameter that can describe the similarity of two sets of samples. When R approaches to 1, it means two samples are more similar with each other. The relationship between R and C is shown in Eq.(3):

(2)

(3)

The correlation coefficients of the mobile-call distribution of each day are computed respectively shown in Table 4. The highest R among these 4 days are 0.9905 and 0.9899, respectively the correlation coefficients between Day 1 and Day 2, Day 3 and Day 4, which prove the visual result that the mobile-call distributions in weekends are different from them in workdays. These differences of mobile-call distributions between workdays and weekends indicate the macro differences of human behavior.

Table 4 The correlation coefficients of each day

2.2 The fitting of mobile-call data

After plotting the distributions of mobile call are plotted shown in Fig.4, all the statistical points distribute on one bimodal curve, which is called ‘the typical human circadian rhythm’.

In this paper, curves of the distribution of mobile calls are treated as signals. As we know, a signal can be decomposed into its component frequencies with Fourier function. While at the macro level, the distribution curve is formed up by different patterns of usage models, which is similar to signals. By using Fourier function, the macroscopic phenomena can be described, the collection of all individual behaviors can be described. It is also helpful that we may find the major patterns of usage models in future work.

The bimodal curve can be well fitted by a 5-order Fourier function,

(4)

where a0, a1, b1, a2, b2, a3, b3, a4, b4, a5, b5and w are the free parameters listed in Table 5. In Fourier function parameters a1, b1, a2, b2, a3, b3, a4, b4, a5and b5indicate amplitudes, w indicates the frequency and a0indicates the displacement. There are seven similar parameters (a0, a1, b1, a3, b3, a4and a5) between Day 1 and Day 2, five similar parameters (a0, a3, b3, b4and a5) between Day 3 and Day4. Besides, there are three individual similar parameters (b2, b5and w) between Day 2 and Day 3, one individual similar parameter (b2) between Day 1 and Day 4. Meanwhile, parameters without marking indicate the most prominent features of the distribution that is different from other ones (e.g.,a0, a2, b5and w are the prominent features of Day 1).

The Fourier function is the study of the way that general functions may be represented or approximated by sums of simpler trigonometric functions often used in signal processing. Although the fitting parameters of the Fourier function are able to describe this signal (distribution), it is difficult to relate these parameters with certain factors. That is, these parameters are only used as indexes of measurement while the physical meanings of them are not studied and explained in our work.

(X-axis is real time; Y-axis is the proportion of calls)

ParaDay1Day2Day3Day4a01.151e-051.158e-051.157e-051.154e-05a1-7.112e-06-7.279e-06-6.834e-06-5.945e-06b1-8.491e-06-8.584e-06-8.514e-06-8.807e-06a21.371e-061.841e-062.779e-062.446e-06b2-2.609e-06-2.222e-06-2.2e-06-2.767e-06a3-1.741e-06-1.644e-06-2.392e-06-2.53e-06b31.841e-061.975e-061.039e-069.686e-07a4-7.688e-07-7.426e-082.539e-07-2.125e-07b4-1.77e-06-2.037e-06-1.535e-06-1.629e-06a51.931e-081.291e-08-1.493e-07-2.493e-07b57.999e-076.585e-076.277e-071.021e-06w7.118e-057.278e-057.27e-057.235e-05SSE4.432e-083.521e-084.581e-084.912e-08R-Square0.99290.99450.99260.9918RMSE7.163e-076.384e-077.282e-077.54e-07

In order to obtain more accurate distributions, two significant periods are chosen to study. One is the rising period of distribution from 8:00 to 10:00; the other is the declining period of distribution from 22:00 to 24:00.

The reason why we chose these periods are: 1) distribution curves in these periods are similar to each other; 2) they are linearly rising and declining periods by observation. These distributions are well fitted by a Polynomial function,

P=Kx+a

(5)

Parameter K is the slope of the fitting curve and a indicates the displacement which is not important in this case. The fitting curves and their indicators of the rising and declining periods are shown in Fig.5, Table 6 and Fig.6, Table 7 respectively.

(X-axis is real time; Y-axis is the proportion of calls)

ParaDay1Day2Day3Day4K8.797e-068.956e-067.977e-068.24e-06SSE2.534e-091.655e-092.874e-092.442e-09R-Square0.98630.99150.98150.9852RMSE5.933e-074.795e-076.318e-075.824e-07

(X-axis is real time; Y-axis is the proportion of calls)

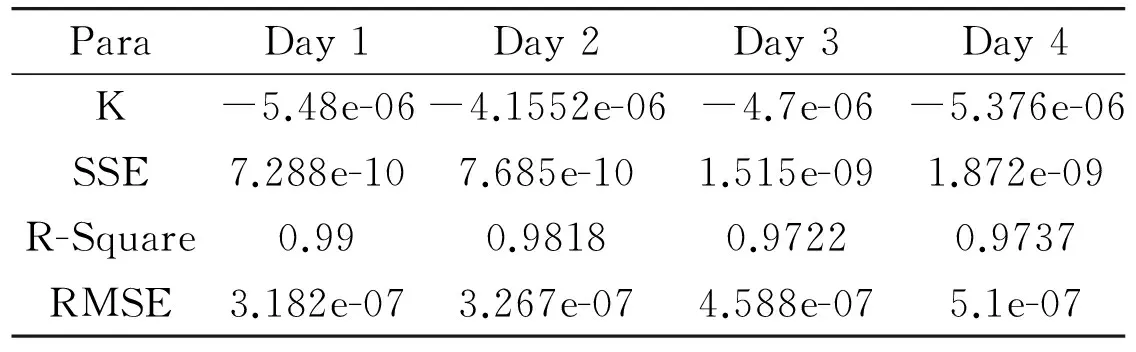
ParaDay1Day2Day3Day4K-5.48e-06-4.1552e-06-4.7e-06-5.376e-06SSE7.288e-107.685e-101.515e-091.872e-09R-Square0.990.98180.97220.9737RMSE3.182e-073.267e-074.588e-075.1e-07

It is noticed that there is a significant difference of K between Day 1, Day 2 and Day 3, Day 4 in the rising period. K of Day 3 and Day 4 is much lower than that of Day 1 and Day 2, that is, the activity levels of users in workdays increase more rapidly than that in weekends. At the same time, K of Day 1 and Day 4 is much lower than that of Day 2 and Day 3 in the declining periods, the result indicates that the activity levels of users depend on whether the next day is weekend.

Besides, K of Day 3 is lower than that of Day 4 in the rising period while K of Day 3 is higher than that of Day 4 in the declining period. That is, the increasing of activity level in Day 3 is slower than that in Day 4. Meanwhile, the decreasing of activity level in Day 4 is quicker than that in Day 3. The result indicates that users are more ‘relaxed’ in Day 3 (Saturday) than that in Day 4 (Sunday).

3 The measurement of mobile-internet data

In the measurement of mobile-internet data, the correlation analysis and fitting are experimented. Besides, the traffic with the online time is measured where an interesting observation shows that the mobile-internet traffic does not monotonically increase over the online time. The measurement shows that the mean traffic of mobile-internet surfing increases with the online time ranging from one hour to eight hours. When the online time reaches to 8 hours, the mean traffic of mobile-internet surfing approaches to its maximum value about 57.4MB. After that, it is a general downward trend of the traffic against online time (in our research, the longest mobile-internet online time for an individual in our data is about 54,000s). The 95% confidence interval graph for traffic-time distribution is shown in Fig.7.

(X-axis is the service time; Y-axis is the mean traffic)

The result indicates that when the online time of an individual comes to about 2 hours per day, the mean internet-mobile traffic reaches the maximum. This result may helpful for studying the use model of mobile-internet, and it is valuable for operators to design their mobile-internet services.

3.1 Correlation analysis of mobile-internet data

Eqs(2,3) are used to compute the correlation coefficients of the mobile-internet distribution of each day shown in Table 8. The correlation coefficients of those distributions are much lower than those of mobile calls. The highest R, between Day 1 and Day 3, is 0.8592. The rule that there are differences of mobile-call distributions between workdays and weekends is not observed in correlation coefficients of mobile-internet distributions.

Table 8 The correlation coefficients of each day

3.2 The fitting of mobile-internet data

Here the same 5-order Fourier function is used to fit the distribution of mobile-internet surfing shown in Fig.8 and Table 9, the formula and parameters of which are the same as that we used in the fitting of mobile-call distributions.

Relatively similar parameters are also marked in each row in bold and underlines. There are two similar parameters (b1, b4) between Day 1 and Day 2; two similar parameters (a0, b4) between Day 3 and Day 4; one similar parameter (b2) between Day 2 andDay 3; four similar parameters (b1, a3, a4, b5) between Day 1 and Day 4; three similar parameters (b1, a4, a5) between Day 2 and Day 4. Parameters without marking indicate the most prominent features of the distribution that is different from other ones. The use of Fourier function is still facing the problem of corresponding parameters to certain factors.

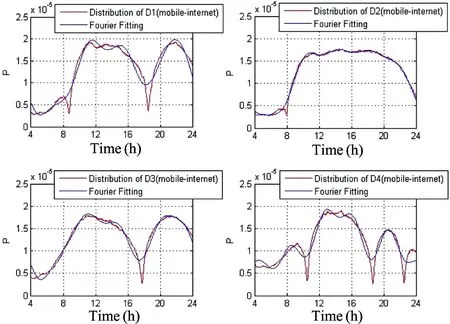
(X-axis is real time; Y-axis is the proportion of mobile-internet surfing)

ParaDay1Day2Day3Day4a01.253e-057.207e-061.237e-051.19e-05a1-1.438e-06-1.318e-05-1.504e-062.57e-07b1-5.318e-06-4.926e-06-3.383e-06-4.791e-06a25.214e-06-4.777e-064.442e-06-1.096e-06b2-4.89e-07-1.657e-06-2.485e-061.369e-06a33.05e-07-3.365e-06-2.296e-075.274e-07b3-1.103e-065.568e-07-7.197e-071.993e-06a4-3.658e-07-2.55e-06-9.659e-07-3.399e-07b4-9.872e-07-8.047e-072.364e-074.691e-07a5-1.018e-06-4.498e-073.119e-075.857e-07b51.115e-06-1.013e-069.674e-071.891e-06w7.37e-056.389e-057.313e-058.907e-05SSE9.733e-081.803e-085.319e-081.473e-07R-Square0.96010.99140.96560.8942RMSE1.163e-065.005e-078.596e-071.431e-06

3.3 Features of users at troughs

The distributions of the mobile-internet surfing are not completely unregular. The main difference between these distributions is that there exist strange troughs in Day 1, Day 3, and Day 4. This troughs, not obvious in coarse-scaled plots, haven’t been described in existing models. In consideration of the sample size, some features of active users at these troughs are just analyzed and listed in Table 10.

Active users from 8 obviously troughs are collected. It is found that these users spend much more time on mobile-internet surfing than others in average. The average sum online time of mobile-internet surfing for each user in these 4 days is 19340s, and the average sum traffic of mobile-internet using for each user is 37001kB, and the average sum online time of those users are much more than that of average users. But the average mobile-internet traffic they spend has no obvious difference with that of other users.

An interesting discover is that the average of those users are all above 90%, which means most of those users prefer to use mobile-internet much more than mobile calls.

Table 10 Features of troughs-users in the distribution of mobile-internet surfing

4 Conclusion

Mobile-internet now performs an important role in the use of mobile phones. Through the analysis of associated mobile data, the frequency of using mobile call and mobile-internet is firstly normalized. It is found that over 86% of users is prone to using either the mobile call or mobile-internet surfing, which is complied with the Pareto Law.

Then great difference is found between the patterns of workdays form and those of weekends by comparing their correlation coefficients and fitting parameters. The results show that the active level of users between workdays and weekends is different, even different between Saturday and Sunday.

By analyzing active users at troughs of the distribution of mobile-internet, it is found that most of users spend much more time on mobile-internet surfing and less time on mobile call. It is also found that the mobile-internet traffic does not monotonically increase over online time. When the online time of mobile-internet comes to about 2 hours per day, the mobile-internet traffic approaches to the maximum value.

All these results are helpful to related practitioners, especially service providers to design their strategies and push bundled services to different users at different time.

[ 1] Candia J, González M C, Wang P, et al. Uncovering individual and collective human dynamics from mobile phone records. Journal of Physics A: Mathematical and Theoretical, 2008, 41(22): 224015

[ 2] Jo H H, Karsai M, Kertész J, et al. Circadian pattern and burstiness in mobile phone communication. New Journal of Physics, 2012, 14(1): 013055

[ 3] Onnela J P, Saramäki J, Hyvönen J, et al. Analysis of a large-scale weighted network of one-to-one human communication. New Journal of Physics, 2007, 9(6): 179

[ 4] Motahari S, Zang H, Reuther P. The impact of temporal factors on mobility patterns. In: Proceedings of the 45th Hawaii International Conference on System Science. IEEE, Hawaii, USA, 2012. 5659-5668

[ 5] Olmedilla D, Frías-Martínez E, Lara R. Mobile web profiling: A study of off-portal surfing habits of mobile users. In: Proceedings of the User Modeling, Adaptation, and Personalization. Springer Berlin Heidelberg, 2010. 339-350

[ 6] Duggan M, Smith A. Cell internet use 2013. Washington, DC: Pew Research Centerl, 2013

[ 7] Taylor C A, Anicello O, Somohano S, et al. A framework for understanding mobile internet motivations and behaviors. In: CHI’08 Extended Abstracts on Human Factors in Computing Systems (CHI EA’08), New York, USA, 2008, 2679-2684

[ 8] Ghose A, Han S P. An empirical analysis of user content generation and usage behavior on the mobile Internet. Management Science, 2011, 57(9): 1671-1691

[ 9] Hsu S L, Doong H S, Wang H. Exploring diffusion patterns of 3G wireless Internet service adoption. In: Proceedings of the 2nd IEEE International Conference on Computer Engineering and Technology, Chengdu, China, 2010. 6: 142-144

[10] Wang C. Surfing mobile internet motivated by fashion attentiveness: An empirical study of mobile internet use in China. In: Proceedings of the 8th International Telecommunications Society (ITS) Asia-Pacific Regional Conference, Taipei, China, 2011

[11] Purcell K, Smith A, Zickuhr K. Social media & mobile internet use among teens and young adults. Millennials. Pew internet & American life project, 2010: 1-37

[12] Ishii K. Internet use via mobile phone in Japan. Telecommunications Policy, 2004, 28(1): 43-58

[13] Halvey M, Keane M T, Smyth B. Predicting navigation patterns on the mobile-internet using time of the week. In: Proceedings of the Special Interest Tracks and Posters of the 14th International Conference on World Wide Web, New York: ACM, 2005. 958-959

[14] Ramsay M, Nielsen J. WAP Usability, Déjà Vu: 1994 All Over Again. Nielsen Norman Group, 2000. 1-90

[15] De Jonge E, van Pelt M, Roos M. Time patterns, geospatial clustering and mobility statistics based on mobile phone network data. In: Proceedings of the Paper for the Federal Committee on Statistical Methodology Research Conference, Washington, USA, 2012

[16] Halvey M, Keane M T, Smyth B. Mobile web surfing is the same as web surfing. Communications of the ACM, 2006, 49(3): 76-81

[17] Jiang Z Q, Xie W J, Li M X, et al. Calling patterns in human communication dynamics. Proceedings of the National Academy of Sciences, 2013, 110(5): 1600-1605

[18] Chung J Y, Choi Y, Park B, et al. Measurement analysis of mobile traffic in enterprise networks. In: Proceedings of the IEEE 13th Asia-Pacific Network Operations and Management Symposium, Taipei, China, 2011. 1-4

[19] Verkasalo H. Contextual patterns in mobile service usage. Personal and Ubiquitous Computing, 2009, 13(5): 331-342

[20] Halvey M, Keane M T, Smyth B. Time based patterns in mobile-internet surfing. In: Proceedings of the SIGCHI Conference on Human Factors in Computing Systems. Montréal, Canada, 2006. 31-34

Song Zhu, born in 1983, He received his M.S. degree from University of Electronic Science and Technology of China in 2008. He is presently staying in University of Electronic Science and Technology of China to study data mining, modeling for his doctoral degree in information security. His main research interests include data mining/analyzing and traffic modeling/simulation.

10.3772/j.issn.1006-6748.2015.02.007

①Supported by the National High Technology Research and Development Programme of China (No. 2011AA010706) and the National Natural Science Foundation of China (No. 61170041).

②To whom correspondence should be addressed. E-mail: toni110@163.com Received on Dec. 23， 2013, Qin Zhiguang, Luo Jiaqing, Zhang Yuehan