气垫调压室临界稳定断面计算参数取值讨论

张 健，于德爽，安建峰

(河海大学水利水电学院，江苏南京 210098)

在含有调压室的引水发电系统中，调压室断面面积不仅需满足其波动稳定性要求，还需满足涌浪幅值控制要求［1］。但是，对气垫调压室而言，由于顶部高压气垫对水位波幅的抑制作用，其断面面积通常只取决于临界稳定断面［2-3］。若实际断面面积小于该临界值，则调压室水位发生微幅扰动后波动将无法衰减，从而导致水力共振和调压室失稳事故［1-2］。

气垫调压室水位发生波动时不同时刻室内气体的热力学状态可用理想气体状态方程描述，但是状态方程无法描述气体的热力学过程［4］，难以获得调压室的水位变化情况。为此，澳大利亚学者Graze［5］曾提出使用有理热传导方程描述气体的热力学过程，在不增加变量的情况下，根据气体和边壁之间的热传递函数得到气体体积和压力的关系。但是，该方法涉及因素较多，且热传递函数较难确定［2］。因此，通常情况下采用多方过程方程描述气体不同状态之间的热力学变化过程，并据此推求气垫调压室的临界稳定断面［6-7］。研究结果表明，多方指数为1.4和1.0分别表征气体绝热和等温变化，且多方指数取值越大则临界稳定断面面积越大，故工程上大多取多方指数为1.4确定气垫调压室的断面面积，以策安全［8-9］。

实际上，气垫调压室水位波动周期较长，在此过程中气体不可能完全绝热，其与环境之间不可避免地存在热交换，故多方指数的上述取值与实际不符，由此得到的气垫调压室断面尺寸偏于保守［3，10］。另外，由于气室常数项中隐含电站静水头和机组引用流量，故气垫调压室临界稳定断面中电站静水头取最小值、机组引用流量取最大值可能无法保证气垫调压室在电站所有可能运行条件下的波动稳定性［11-12］。

针对上述情况，本文通过分析气垫调压室水位小波动过程中的气体温度变化过程及其临界稳定断面公式，明确多方指数取值对波动稳定后气室最终温度的影响，确定电站静水头和机组引用流量取值对稳定断面面积的影响规律，并讨论上述参数的合理取值，为工程设计提供依据。

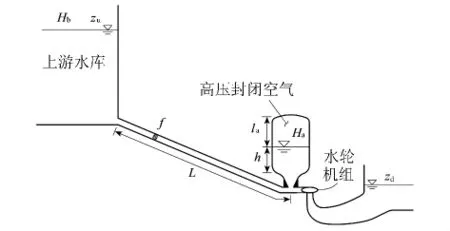
图1 含气垫调压室的引水发电系统示意图Fig.1 Sketch of hydropower system with an air-cushion surge chamber

1 气垫调压室临界稳定断面

图1为含气垫调压室的引水发电系统示意图，其中zu、zd分别表示上游库水位、下游尾水位，L和f分别表示引水道的长度及其断面面积，Hb表示当地大气压力水头，la、Ha、h分别表示气垫调压室气体高度、绝对压力水头、调压室水深。对图示系统作如下假设:(a)忽略调压室内水体惯性和调压室阻抗;(b)波动过程中水轮机效率保持为常数;(c)水电站单独运行，调速器绝对灵敏，使水轮机出力保持不变;(d)波动的幅度极小，可忽略所有高于二阶的微分量。

气垫调压室在运行过程中需满足如下基本方程:

动力方程

连续方程

气体多方过程方程

等出力方程

式中:zt——气垫调压室顶部当量高程，m;Qt、Q——机组引用流量、引水道流量，m3/s;v——引水道流速，m/s;α——引水道阻抗系数，s2/m5;As——调压室断面面积，m2;x——调压室水位微小变量，m;hwm——调压室水位波动时的压力管道水头损失值，m;ΔHa、q——调压室水位波动引起的气室绝对压力水头、机组引用流量微幅变化;Q0、hwm0——电站初始稳定运行时的流量及压力管道水头损失;m——理想气体多方指数;C——常数，对质量不变的气体，该值不变。

由方程(1)～(4)结合电站稳定运行时满足的条件，可得到气垫调压室临界稳定断面面积:

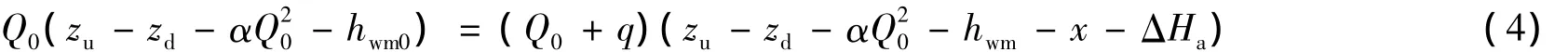
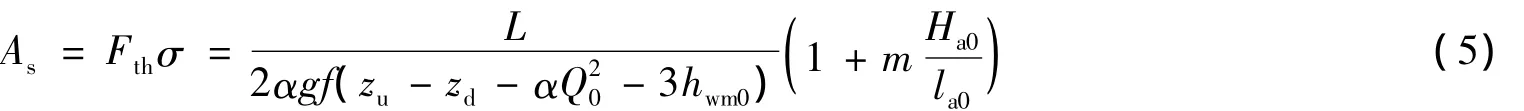
式中:Fth——相应于常规开敞式调压室的临界稳定断面(托马断面)［1］;σ——气室常数。

2 多方指数取值分析

以T0表示环境温度，Ta表示气垫调压室水位波动过程中气体温度。Ta、Ha、la中加入下标“0”表示电站初始稳定运行状态下的参数值，下标“s”表示采用多方指数方程描述气体热力学过程时气垫调压室水位波动趋于稳定后的参数值，下标“e”表示实际调压室波动稳定后的参数值。

电站初始稳定运行时Ta0=T0，Ha0、la0满足:

且有

任意状态下气室参数满足理想气体状态方程，故

式中［C*］为常数，主要反映气垫调压室内的气体质量大小。

视气体状态变化过程为无数多个稳定状态沿时间序列的叠加，则式(7)和式(8)在调压室水位波动初始状态和最终稳定状态之间同时满足，由此可得波动稳定时的气体温度:

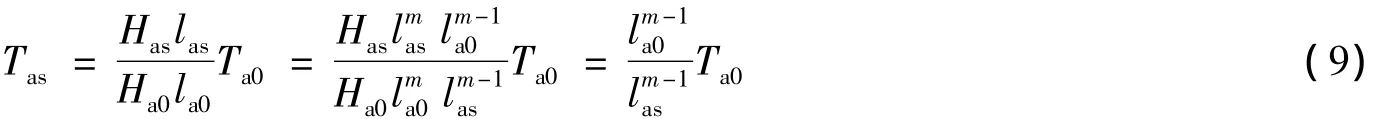
显然，若多方指数取1.0，调压室水位波动过程中气室温度不变，且始终与环境温度保持一致;若多方指数取1.4，机组正常运行过程中负荷突然微幅减小，则机组引用流量将减小，引水道水头损失减小。此情况下，由式(6)可知初始和波动稳定状态下气室参数满足:

由式(7)和式(10)可得

考虑到函数f(x)=k/xm-x为单调递减函数，由式(11)可知此时las＜la0，结合式(11)可知在机组负荷突然减小的情况下，调压室水位波动趋于稳定时的气室气体温度高于其初始温度，即Tas＞Ta0。从能量转化角度分析，两种状态相比，调压室水位升高，水体对气体做的功大于气体对水体做的功，而多方指数为1.4，气体与外界绝热，气体内能必然增加，表现为温度升高。

若多方指数取1.4，对机组负荷突增过程做类似分析，可知调压室水位波动趋于稳定时气体温度低于其初始温度。

上述分析表明，当多方指数取1.4，调压室水位波动趋于稳定时室内气体温度与环境温度不同。显然，此稳定状态是无法维持的，温度梯度的存在必然导致气体与外界发生热交换，这将再次引起调压室水位微幅波动，直到气体温度与环境温度一致。这也说明采用绝热过程描述调压室水位微幅扰动时的气体热力学变化过程是值得商榷的。事实上，气垫调压室内气体的实际热力学过程应是调压室水位波动引起的气体状态变化与热交换引起的气体状态变化的耦合作用过程，此过程中多方指数并非固定常数，但是从气体变化的整个过程来看，无论中间经过多少热力学状态变化，最终都必将有Tae=T0。因此，多方指数取1.0，即以等温过程描述气室参数由初始至最终的气体状态变化更符合实际的气体物理过程。

3 电站静水头及机组流量取值分析

为便于分析，只考虑上游库水位变化，并忽略压力管道水头损失项，令C1=L/(2αgf)，H0=zu-zd-αQ20，则有

在调速器绝对灵敏、水轮机效率不变假定下，水轮机出力公式满足

将电站稳定运行时的气室压力Ha0代入多方过程方程，可得

对式(12)、式(13)、式(14)求全微分，整理得到 dAs、dQ0、dla0，将 dQ0、dla0项代入 dAs中整理可得

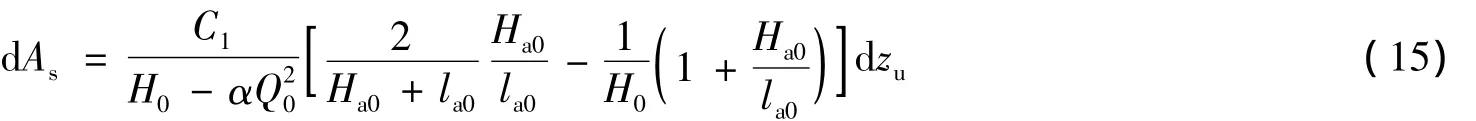
在含气垫调压室的引水发电系统中Ha0/la0≫1，可将气室常数项近似等于Ha0/la0，进一步化简式(15)并移项为微分形式，有

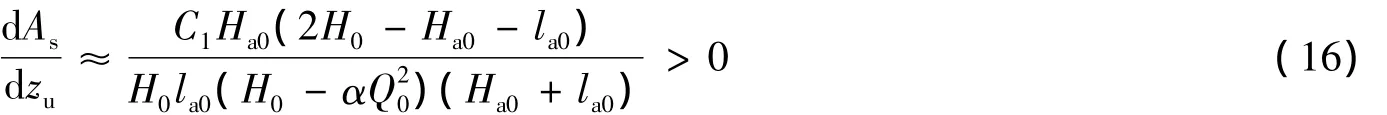
式(16)表明，对于气垫调压室而言，随着上游库水位的取值增大，调压室临界稳定断面将增大。此外，从式(13)可以看出，在机组等出力情况下，电站静水头越大其相应的机组引用流量越小，所以机组引用流量的取值对临界稳定断面的影响与电站静水头相反。因此，应选取电站正常运行时可能出现的最高上游库水位与最低尾水位相组合即电站最大水头作为计算工况来确定气垫调压室的稳定断面，此时电站静水头为最大值，机组流量为最小值，与常规开敞式调压室取值方式不同。

4 算例分析

某含气垫调压室的引水式电站，安装2台冲击式水轮机组，机组额定流量14.98 m3/s，安装高程215.00 m。电站上库最高水位1161.7 m，最低水位1138m。引水隧洞全长17.5km，当量断面面积19.19m2，隧洞进口至隧洞末端平均坡度3.44%，调压室当量高度12.1 m，底板高程562.00 m，引水隧洞阻抗系数0.0138 s2/m5，压力管道阻抗系数0.0136 s2/m5。

结合特征线法和状态方程分析法进行水力-机械系统小扰动数值计算［13-14］，计算条件为:气垫调压室断面面积420m2，环境温度20℃，机组额度水头下额定出力运行2台机同时发生10%负荷扰动，多方指数m分别取1.0、1.2、1.4。由计算结果可得到多方指数取1.4和1.2时的室内气体温度变化过程(图2)，对m=1.0的情况，由于气体等温变化，其温度始终与环境温度相同，不再给出其温度变化过程线。

从图2可以看出，当多方指数取1.4和1.2时，室内气体温度围绕某一波动稳定轴线逐渐衰减，波动稳定轴线的温度值即为调压室水位波动趋于稳定时的理论气体温度。从图中提取温度变化10个周期内的波峰温度和波谷温度及每个温度对应的时间(表1)，并对波峰温度和波谷温度随时间的变化关系分别进行线性拟合，则2条拟合直线的交点温度即波动稳定时的理论气体温度。由线性拟合结果可得m=1.4时Tas=20.28℃，m=1.2时Tas=20.21℃，可见若多方指数取不等于1.0的固定值模拟小扰动下的气体热力学过程，波动稳定时气体温度与环境温度(20℃)不同。而气体的实际物理过程中即使水位波动时气体温度有微小变化，但波动稳定时气体温度与环境温度应是严格相等的，显然，以等温变化(m=1.0)描述气体的热力学过程更符合实际。

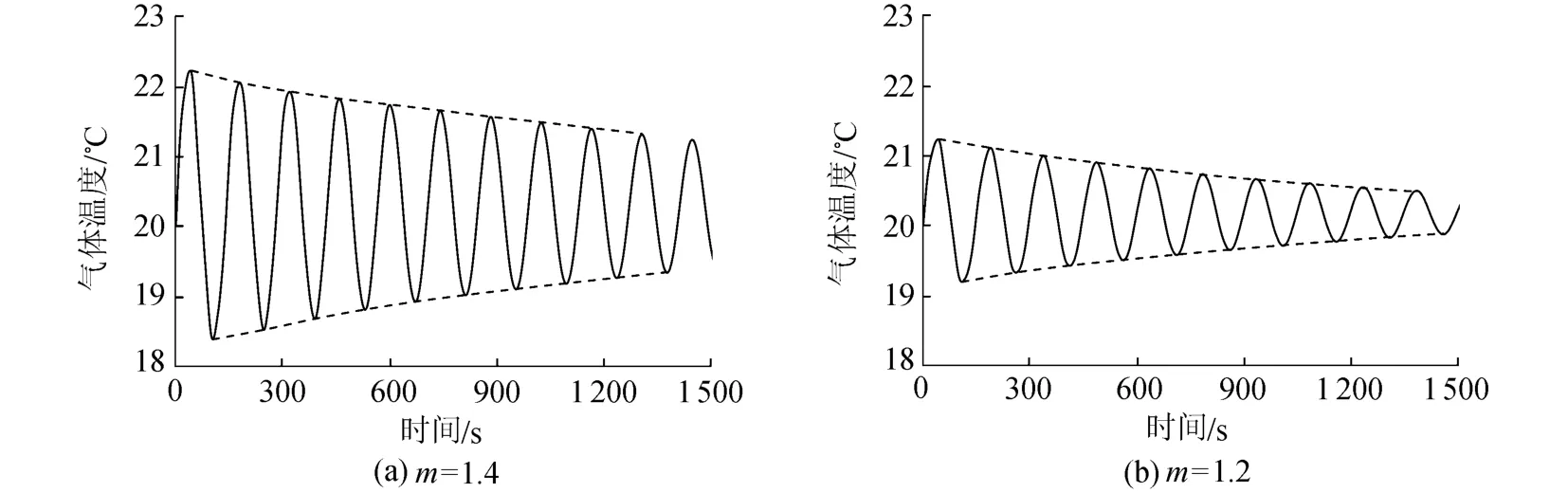
图2 气体温度变化过程(10%扰动)Fig.2 Dynamic process of gaseous temperature(10%perturbation)

表1 气体温度变化10个周期内的温度极值Table 1 Extreme temperature during ten cycle s of dynamic process of gaseous temperature

根据电站基本资料，取多方指数为1.0、调压室安全系数为1.2、室内当量气团质量Ha0la0=3790，计算不同运行工况下所需的气垫调压室临界稳定断面面积，结果见表2。从表2数据可以看出电站静水头的取值对稳定断面各个参数的影响趋势，其中电站静水头越大，相应机组流量越小，所需的稳定断面越大。该结果与理论分析结论一致。

表2 不同计算工况时的稳定断面面积Table 2 Critical stability areas under different conditions

5 结 语

气垫调压室断面面积常取决于其临界稳定断面。在推求临界稳定断面公式时，通常采用气体多方过程方程描述室内气体不同状态之间的热力学变化过程，其中多方指数的大小应依据气体的实际物理过程性质选取。通过分析多方指数取值对机组小扰动时调压室水位波动稳定后气体温度的影响以及对临界稳定断面公式的理论推导，并结合工程实例进行计算分析，结果表明，计算气垫调压室临界稳定断面时气体多方指数应取1.0，电站静水头、机组流量应分别取电站正常运行时的最大值和最小值。

［1］刘启钊.水电站［M］.3版.北京:中国水利水电出版社，2007:225-226.

［2］张健.气垫调压室水力性能研究［D］.南京:河海大学，1999.

［3］AN Jianfeng，ZHANG Jian，HAZRATI A.Safe control of air cushion surge chambers in hydropower systems［J］.Scientia Iranica，2013，20(6):1605-1611.

［4］朱明善.工程热力学［M］.北京:清华大学出版社，1994:91-96.

［5］GRAZE H R.A rational thermodynamic equation for air chamber design［C］//University of New South Wales.Proceedings of the 3rd Australian Conference on Hydraulics and Fluid Mechanics.Sydney，Australia:Institution of Engineers，1968:25-29.

［6］SVEE R.Surge tanKwith enclosed compressed air cushion［C］//STEPHENSON D.Proceeding of the First International Conference on Pressure Surges.Cranfield，Bedtord，England:Br Hydromech Res Assoc，1972:15-24.

［7］CHAUDHRY M H，SABBAH M A，FOWLER J E.Analysis and stability of closed surge tanks［J］.Journal of Hydraulic Engineering，1985，111(7):1079-1096.

［8］刘德有，张健，索丽生.气垫调压室研究进展［J］.水电能源科学，2000，18(4):1-5.(LIU Deyou，ZHANG Jian，SUO Lisheng.Advances in research on air-cushioned surge chamber［J］.International Journal Hydroelectric Energy，2000，18(4):1-5.(in Chinese))

［9］刘德友，张罗彬，陈五一，等.圆管型与廊道型气垫调压室水力性能比较［J］.河海大学学报:自然科学版，2012，40(5):534-538.(LIU Deyou，ZHANG Luobin，CHEN Wuyi，et al.Comparison of hydraulic performance of round pipe-shaped and corridor-shaped air-cushioned surge tanK［J］.Journal of Hohai University:Natural Sciences，2012，40(5):534-538.(in Chinese))

［10］张健，索丽生，郑源，等.气垫调压室内气体动态特性研究［J］.水力发电学报，2004，23(4):97-101.(ZHANG Jian，SUO Lisheng，ZHENG Yuan，et al.Study on gas characters of air-cushioned surge tank［J］.Journal of Hydroelectric Engineering，2004，23(4):97-101.(in Chinese))

［11］范波芹，张健，索丽生，等.含气垫调压室的水电站输水系统小波动稳定分析初探［J］.水利水电技术，2005，36(7):114-115，119.(FAN Boqin，ZHANGJian，SUOLisheng，et al.Stability analysis on small fluctuation of the system with air-cushion surge chamber for hydropower station［J］.Water Resources and Hydropower Engineering，2005，36(7):114-115，119.(in Chinese))

［12］谷兆祺，李欣欣，郭军合.挪威水电工程经验介绍［M］.特隆赫姆:泰比亚出版公司，1985.

［13］ ZHANG Yongliang，MIAO Mingfei，MA Jiming.Analytical study on water hammer pressure in pressurized conduits with a throttled surge chamber for slow closure［J］.Water Science and Engineering，2010，3(2):174-189.

［14］郑源，张健.水力机组过渡过程［M］.北京:北京大学出版社，2008:88-92.