多普勒频率误差对飞行目标参数的影响分析*
李 果,崔书华,沈 思,王 敏
(1 宇航动力学国家重点实验室,西安 710043;2 西安卫星测控中心,西安 710043)
多普勒频率误差对飞行目标参数的影响分析*
李 果1,2,崔书华1,2,沈 思2,王 敏1,2
(1 宇航动力学国家重点实验室,西安 710043;2 西安卫星测控中心,西安 710043)
针对试验靶场中的高精度多测速系统中,多普勒频率测量数据的误差对飞行目标产生影响的问题,建立了多普勒频率误差对目标定速的影响分析计算模型。通过仿真计算及定量分析得出,其产生的误差将直接影响目标定速结果,且影响量值随时间增加而逐渐变大。此方法可为飞行目标的定速情况提供有效的分析手段,也为提高外弹道数据处理精度提供技术支持。
多测速系统;多普勒频率误差;影响分析
0 引言
高精度多测速系统的测速基础是多普勒效应,由一主多副或两主多副构成测速测量体制,主站测速雷达发射连续波信号,经目标应答机转发,由副站测速雷达接收信号并测量多普勒频率,从而获得多个径向速度信息。虽然测量终端的多普勒频率测量精度能达到毫赫兹量级,但在实际测量过程中,多普勒频率的测量精度受到热噪声、频率源的频率稳定度、发射信号谱线宽度、频率源的频率漂移、多路径误差、空间折射误差等多种因素的影响,往往会使测量信号夹杂着随机噪声[1-2],同时目标的飞行速度急剧变化、姿态调整等特征点发生动作时,对多普勒频率的测量精度也有较大影响。文献[3-8]对多测速的轨道计算进行了多种方法的讨论,而文中将从多测速的测量数据的源头,即多普勒频率误差对目标定速产生的影响进行分析,以期为后续的数据处理提供分析手段。
1 多普勒频率
多普勒频率误差会对多测速测量系统的性能产生影响,直至对测量目标参数精度带来影响。测速系统按照二进制格式记录多普勒频率,转换至多测速距离和变化率复原公式为:
(1)
2 影响分析
通过建立多普勒误差引发的飞行目标参数的影响分析模型,并利用航天靶场相关发射方向及布站情况对影响量值进行分析。
2.1 分析模型
建立多测速系统测量方程:
(2)
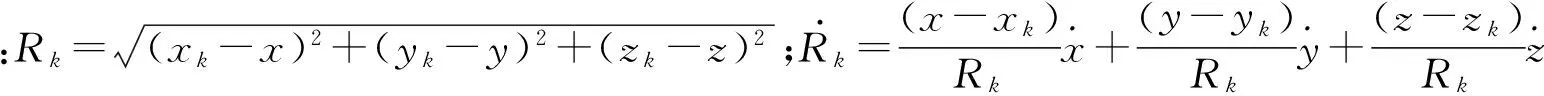
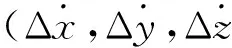
(3)
将式(3)两侧进行微分,并写成矢量形式为:
(4)
式中:
1.2 实例分析
在多测速系统中,主站采用的是双向共源测速模式,这种模式的测速精度较高,多普勒频率误差对目标定速数据的影响极小。副站采用的是双向不共源测速模式[9],这种模式对目标定速数据会产生一定的影响。故文中主要针对副站多普勒频率误差对目标定速结果的影响进行分析。
以某射向、设备布站及跟踪弧段情况为例,分析多普勒频率误差对目标的定速影响。图1~图3为副一站在多普勒频率设计指标δ及2δ、3δ的情况下,目标在X、Y、Z方向的定速偏差。
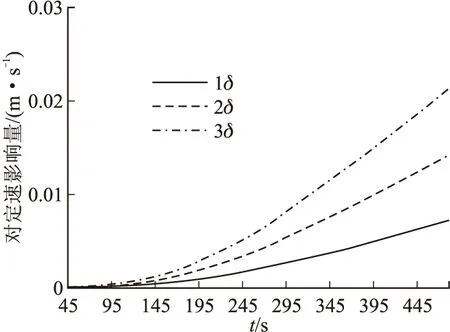
图1 多普勒误差对X方向定速影响图

图2 多普勒误差对Y方向定速影响图
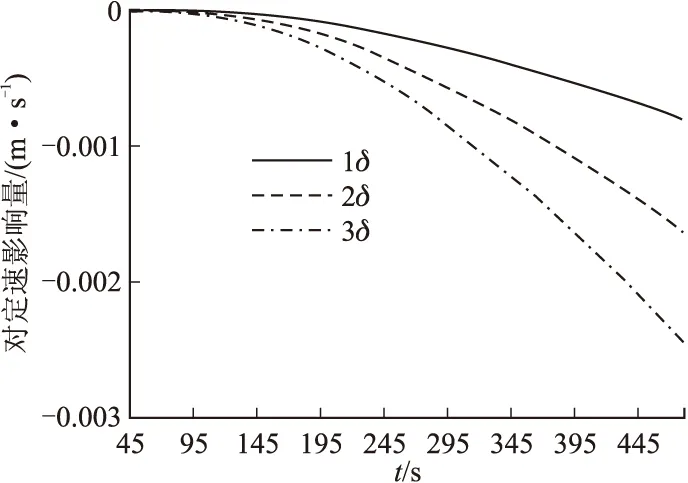
图3 多普勒误差对Z方向定速影响图
从图1~图3中可以看出,副一站多普勒频率误差对Y方向的定速影响较大,对X、Z方向的定速影响较小。具体最大影响量值见表1。
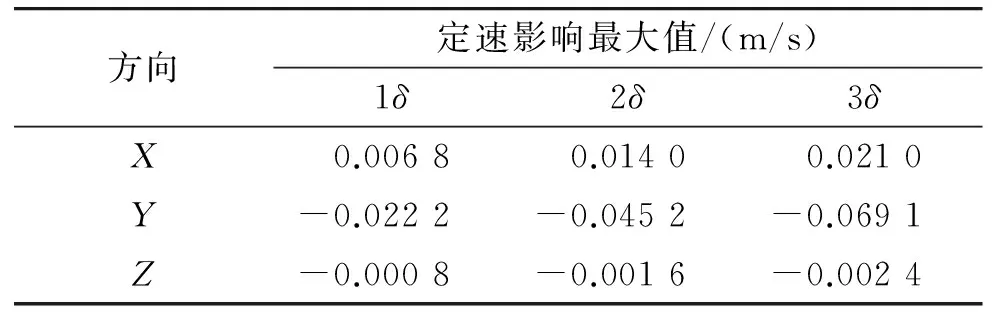
表1 副一站多普勒频率误差对定速影响最大值数据表
图4~图6为副二站在多普勒频率设计指标δ及2δ、3δ的情况下,目标在X、Y、Z方向的定速偏差。

图4 多普勒误差对X方向定速影响图
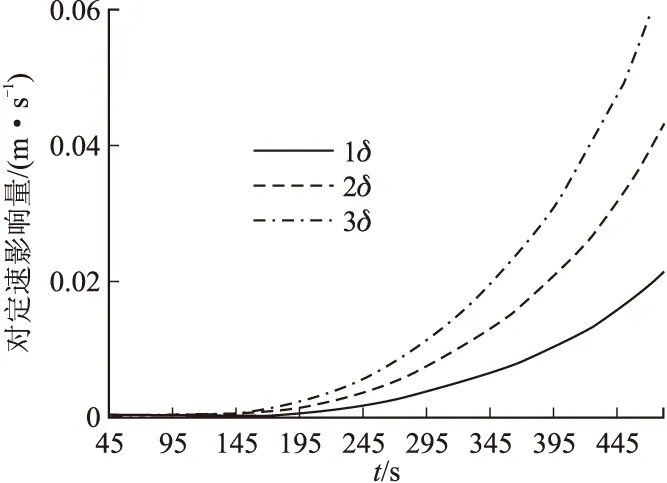
图5 多普勒误差对Y方向定速影响图

图6 多普勒误差对Z方向定速影响图
从图4~图6中可以看出,与副一站相似,副二站多普勒频率误差对Y方向的定速影响较大,对X、Z方向的定速影响较小。具体最大影响量见表2。
图7~图9为副三站在多普勒频率设计指标δ及2δ、3δ的情况下,目标在X、Y、Z方向的定速偏差。
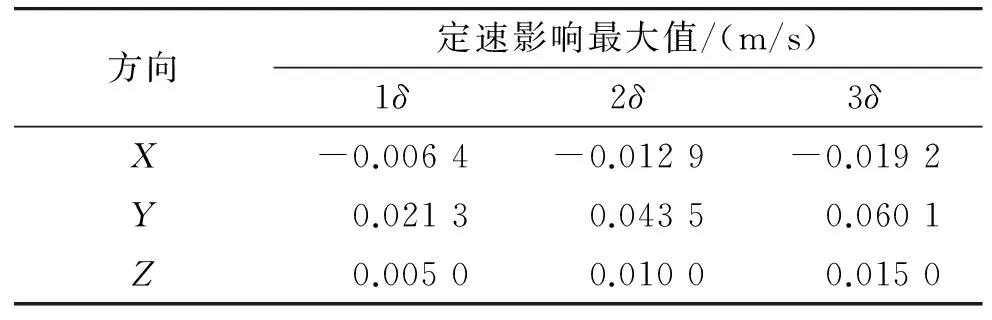
表2 副二站多普勒频率误差对定速影响最大值数据表

图7 多普勒误差对X方向定速影响图
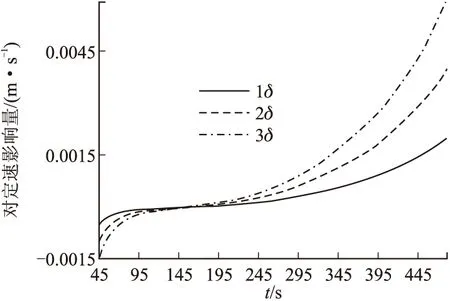
图8 多普勒误差对Y方向定速影响图

图9 多普勒误差对Z方向定速影响图
从图7~图9中可以看出,副三站多普勒频率误差对X、Y、Z三个方向的定速影响都较小。具体最大影响量值见表3。

表3 副三站多普勒频率误差对定速影响最大值
1.3 小结
通过上述分析结果可以看出,多普勒频率误差对副一站和副二站的定速影响较大,当误差量为1δ时,对定速影响最大可达0.02 m/s;当误差量为3δ时,对定速影响最大可达到0.06 m/s,已超出了总体方案要求范围。
3 结论
文中针对多测速测量系统的多普勒频率误差对定速影响进行了定量分析。根据上述分析可以看出,多普勒频率的微小误差就会给目标定速结果带来大的影响,且影响量随时间增加而逐渐变大。因此,利用多测速系统测量数据进行目标定速时,必须对目标飞行过程中出现的过偏数据,以及速度急剧变化、姿态调整等特征点处多普勒频率误差较大的测量数据进行有效处理。
上述分析结果虽然是在某种具体射向及布站情况下得出的结论,但也为后续任务中分析多测速系统的多普勒频率误差对飞行目标的定速影响提供了有力的分析手段,也为提高外弹道数据处理精度提供了技术支持。
[1] 黄富彪, 何兵哲, 秦玉峰. 中低轨卫星多普勒数据处理技术研究 [J]. 微型机与应用, 2012, 31(19): 71-72.
[2] 郭玲红, 李亚立. 单脉冲雷达距离和速度测量精度技术分析 [J]. 航空兵器, 2012(5): 31-33.
[3] 崔书华, 胡绍林, 王敏, 等. 多测速系统测速差分计算及误差分析 [J]. 飞行力学, 2011, 29(6): 89-93.
[4] 崔书华, 胡绍林, 宋卫红, 等. 基于多测速系统最优弹道估计方法及应用 [J]. 弹箭与制导学报, 2012, 32(4): 215-218.
[5] 崔书华, 刘军虎, 宋卫红, 等. 基于拟牛顿方法的非线性求解及应用 [J]. 上海航天, 2013, 30(3): 16-18.
[6] 崔书华, 宋卫红, 刘军虎, 等. 基于最小二乘改进法测速测量数据处理及应用 [J]. 弹箭与制导学报, 2013, 33(1): 159-162.
[7] 崔书华, 胡绍林, 宋卫红, 等. 多测速系统测量数据差分非线性求解及应用 [J]. 导弹与航天运载技术, 2013, 325(2): 64-67.
[8] 梁小虎, 朱武宣, 张艳, 等. 多测速系统中系统误差实时估计与校准算法 [J]. 飞行器测控学报, 2012, 31(5): 49-53.
[9] 李军. 一种测速雷达测量体制应答机的研制 [D]. 成都: 电子科技大学工程, 2011: 17-21.
Analysis of Effect of Doppler Frequency Error on Target Parameter
LI Guo1,2,CUI Shuhua1,2,SHEN Si2,WANG Min1,2
(1 State Key Laboratory of Astronautic Dynamics, Xi’an 710043, China;2 Xi’an Satellite Control Center of China, Xi’an 710043, China)
In view of influence of error of Doppler frequency measurement data on flying target in high-precision multi-velocity measurement system of test range, a calculating model was established to analyze the effect of Doppler frequency error on target speed control. With simulation calculation and quantitative analysis, the resulting error has a direct impact on results of target speed and the impact becomes larger as time goes by. The method offers a new technical means to analyze target speed and provide effective technical support to improve the precision of trajectory data processing.
multi-velocity measurement system; Doppler frequency error; effect analysis
2014-08-23
国家自然科学基金(61473222;61231018;41274018)资助
李果(1982-),男,安徽人,工程师,硕士研究生,研究方向:外弹道数据处理,雷达数据处理。
V557
A

