矿井搜救探测机器人驱动系统最小能耗建模与影响因素分析

苏学满，孙丽丽

SU Xueman1，2,SUN Lili1

1.安徽工程大学 机械与汽车工程学院，安徽 芜湖241000

2.安徽工程大学 机器人产业技术研究院，安徽 芜湖241000

1.School of Mechanical and Automotive Engineering,Anhui Polytechnic University,Wuhu,Anhui 241000,China

2.Institute of Technology Robotics Industry,Anhui Polytechnic University,Wuhu,Anhui 241000,China

1 引言

机器人在工作或行走时，需要有可靠的能量供给，如何有效地使用有限的能源能量，延长机器人的运行时间变得至关重要[1]。分析、控制关节驱动系统的耗散能量并使之最小化，符合系统能量优化工程和电机系统节能工程的实际需要。针对伺服电机和减速器为主体的驱动系统而言，电机的热损耗和非线性摩擦损耗直接限制了系统对电能的有效利用。研究、分析电流热效应、粘性阻尼摩擦、库仑摩擦对系统能耗的影响，明确其作用关系，是能量优化规划得以实施的前提条件[2]。如何运用最优控制理论和方法，动态规划关节驱动系统的能耗使之最小化，已经成为研究中的重点问题之一。

综合国内外研究，多数学者在机器人路径规划及步态等方面进行了能量消耗问题的研究，并提出了很多有价值的研究成果。文献[3-6]从轨迹规划方面研究机器人的能量最优控制；文献[7]通过优化机器人步态参数使系统能量消耗最小；文献[8]利用路径规划方法研究机器人局部区域能量最小化问题；文献[9-11]通过力矩分配方法使系统能耗最小。对机器人运动控制方面的耗能研究，文献[1]利用梯形升降速算法研究速度函数与伺服电机耗能之间的关系；文献[12]研究机器人运动过程中的总动作时间和消耗能量在某种程度上达到综合最优；文献[13]对不同加速控制算法下的最小能耗进行了研究。深入研究机器人最小能耗的影响因素是必要。

本文以六足矿井搜救探测机器人关节驱动系统（直流伺服电机＋齿轮减速器）为研究对象，分析在负载转矩作用下，非线性摩擦和电流热效应对系统能耗的影响，建立关节驱动系统动力学模型，并应用最优控制相关理论和求解方法，建立最优控制电流和角速度函数，以及驱动系统在点到点运动控制模式下的最小能耗模型。

2 关节驱动系统最小能耗模型

2.1 关节驱动系统数学模型

六足矿井搜救探测机器人结构如图1 所示。机器人每条腿具有单独驱动系统，其驱动系统由直流伺服电机通过齿轮减速器驱动轮腿运动，如图2 所示。

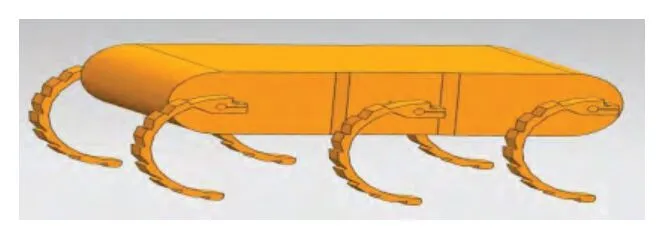
图1 六足矿井搜救探测机器人结构

图2 机器人驱动系统原理图

图2 中Jm、JL为电机转动惯量和负载的等效转动惯量；Bm、BL为电机粘性阻尼系数和传动装置的等效粘性阻尼系数；Tm、TL为电机的电磁转矩和负载转矩；为电机和负载的转速；N为减速比。则驱动系统的转矩平衡方程：

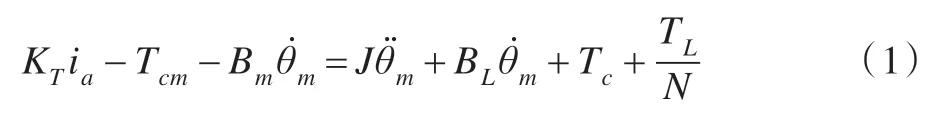
式中ia为电枢电流，J为系统总的转动惯量，Tcm电机库仑摩擦力矩，Tc减速器的库仑摩擦力矩。根据减速器的效率η计算公式：

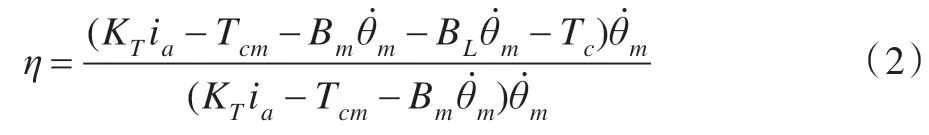
由式（3）和（4）得驱动系统的动态方程为：

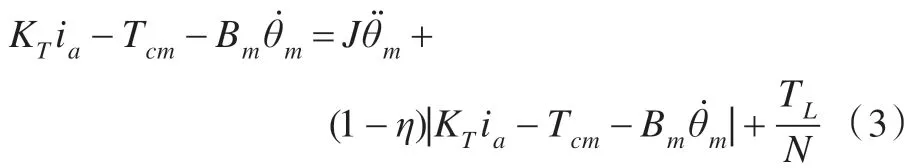
电机驱动的机器人关节驱动系统的能量消耗分为电机绕组产生的热损耗和克服外力做功。则驱动系统在时间[0,tf]内的能量消耗为：

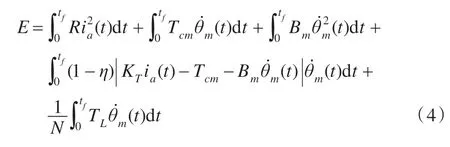
式中第一项为电机绕组产生的热量，第二项为克服电机库仑摩擦力矩做功，第三项为克服电机粘性摩擦转矩做功，第四项为克服减速器库仑摩擦力矩和粘性摩擦转矩做功，第五项为克服负载转矩做功。

为了使驱动系统能量消耗E最小，需要求解能量最小条件下的最佳加减速速度轮廓[14]，即为寻找一个速度函数，在满足的条件下，要求电动机单周期能量消耗E最小。下面利用最优控制理论和最小值定理求解最佳的速度函数以及对应的电枢电流函数。建立驱动系统的最小能耗的模型。

2.2 最优速度和最优电流函数求解

当电机处于加速阶段时，电机的电磁转矩比摩擦转矩（库仑摩擦转矩和粘性摩擦转矩）大。当电机处于减速阶段时，电机的电磁转矩比摩擦转矩小。加减速阶段的速度记为，电流记为ia+(t)、ia-(t)。

若令x1(t)=θm(t)，，则系统加减速阶段的状态方程为：

利用最小定理和哈密顿函数[15]可求解出加减速阶段的速度和的通解：

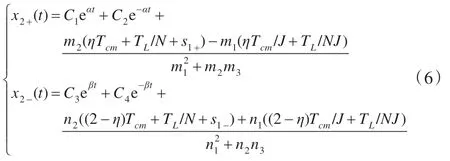
根据初始边界条件x2+(0)=0，x2-(tf)=0，可求得式（6）中的s1+和s1-为：

式（6）变为：

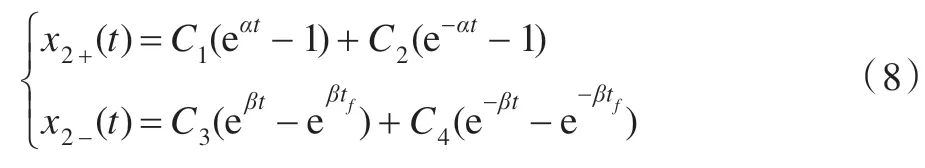
令tc为最佳角速度转换时间，即当t=tc时，直流电机的加速度和减速度均为0。

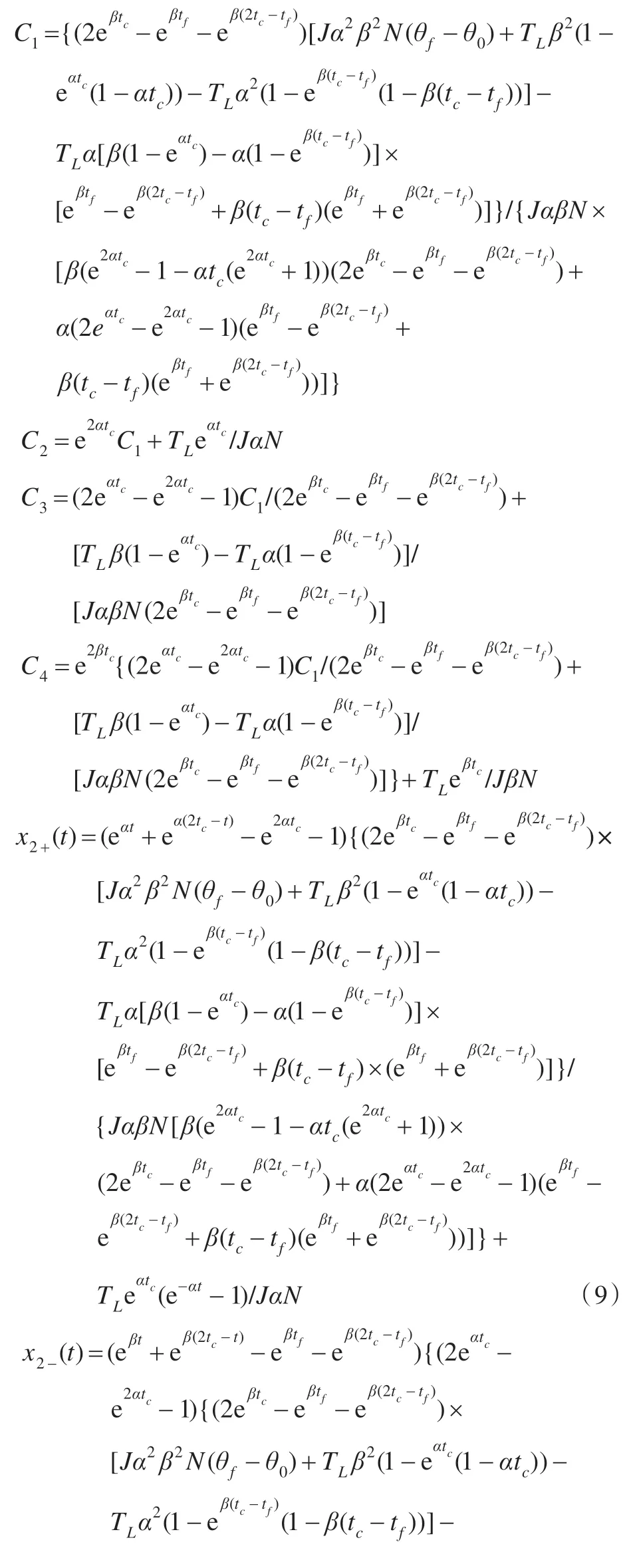
再利用速度函数与电流函数之间的关系，可求得最优电流ia+(t)和ia-(t)关于时间表达式为：

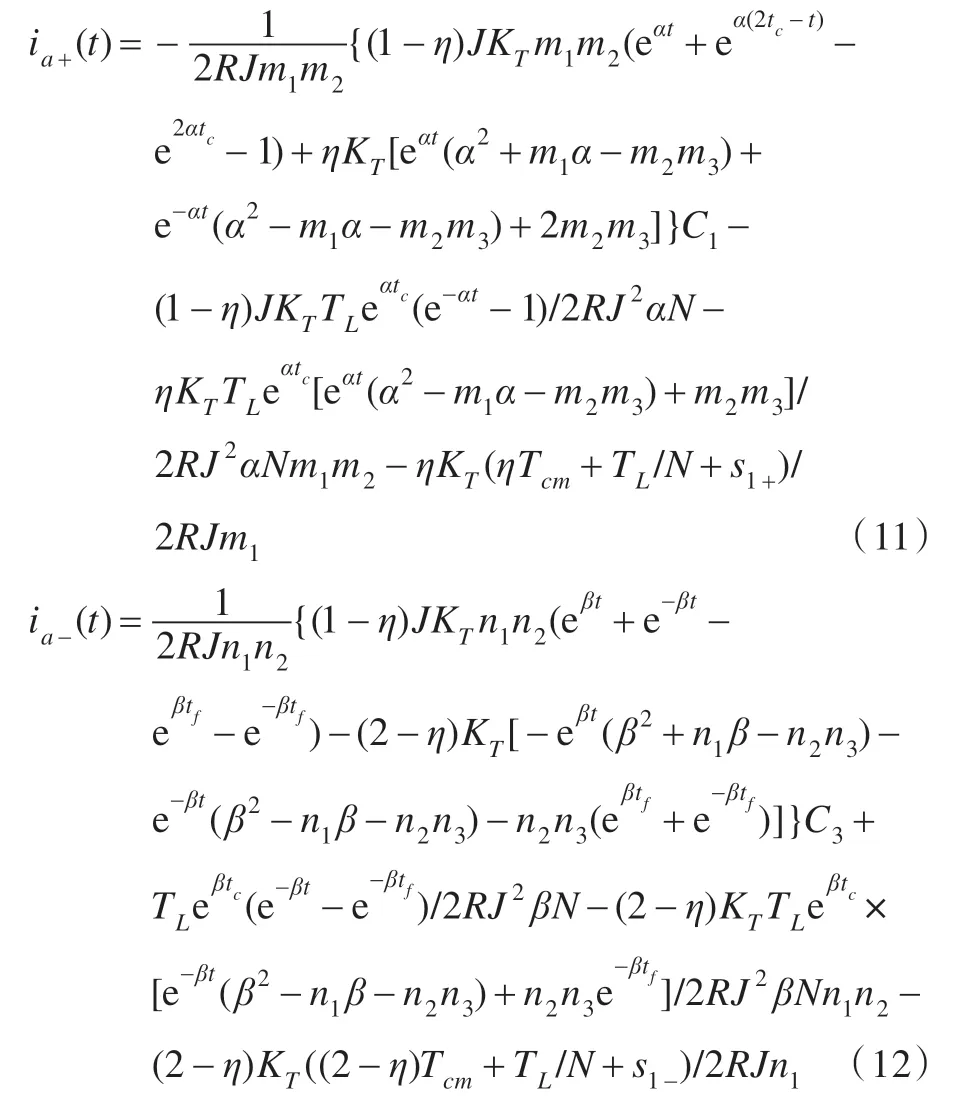
式（9）、（10）、（11）、（12）分别为考虑粘性摩擦和库仑摩擦条件时，基于能耗最小的驱动系统最优加减速速度和最优电流关于时间的函数表达式。

2.3 最小能耗模型

同时考虑粘性摩擦损耗和库仑摩擦损耗，伺服系统总能耗由四部分能耗组成：焦耳热损耗ER、库仑摩擦损耗EC、粘性摩擦损耗EB、负载损耗EL。根据所求的速度和电流函数表达式（9）、（10）、（11）、（12）代入式（5）可求出驱动系统的最小能耗函数表达式。

焦耳热损耗ER的计算如下：

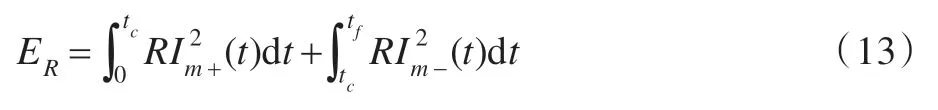
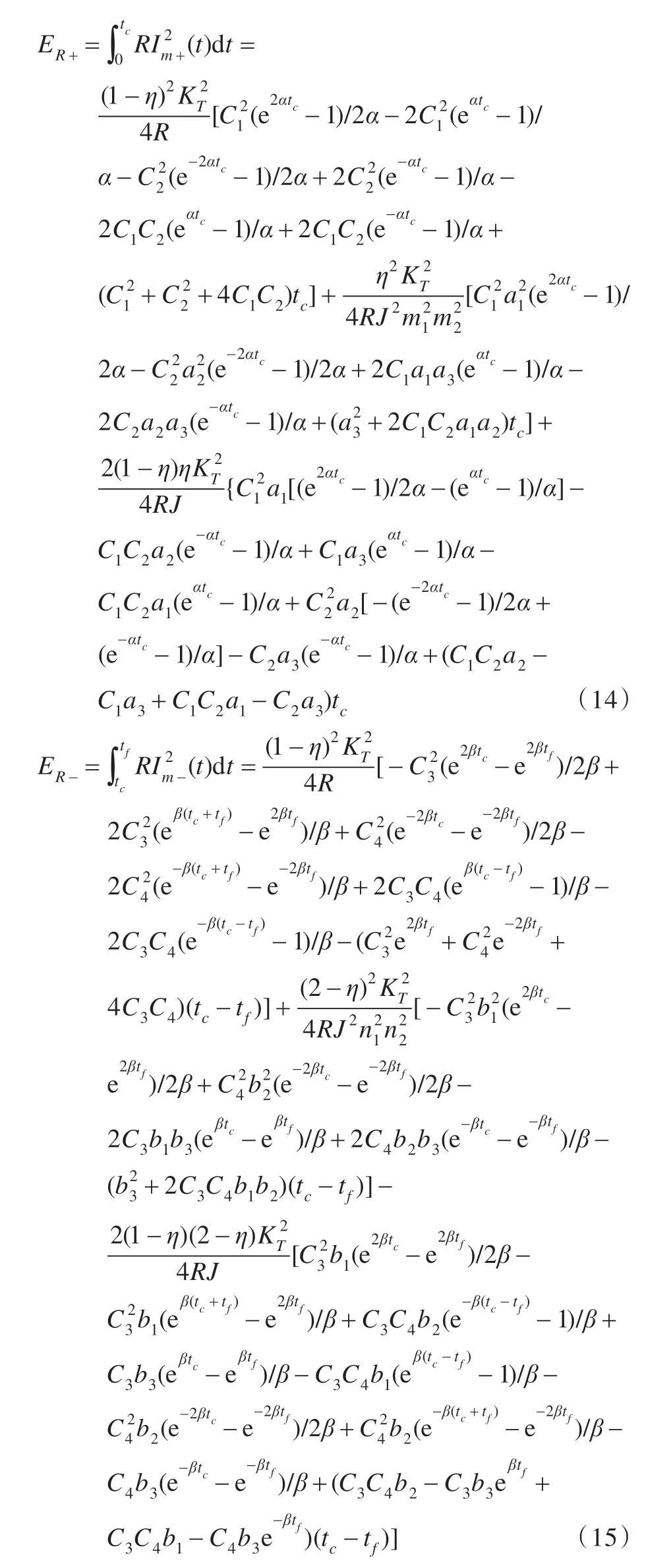
式（14）、（15）分别为加速阶段和减速阶段的焦耳热损耗。

库仑摩擦损耗EC计算如下：

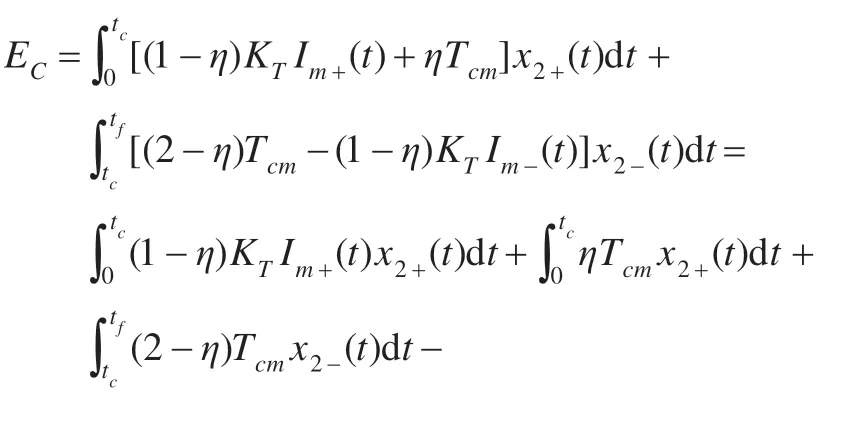
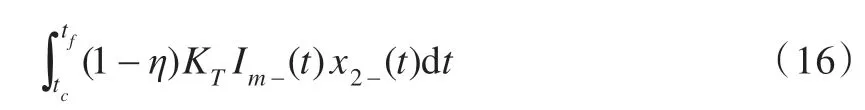
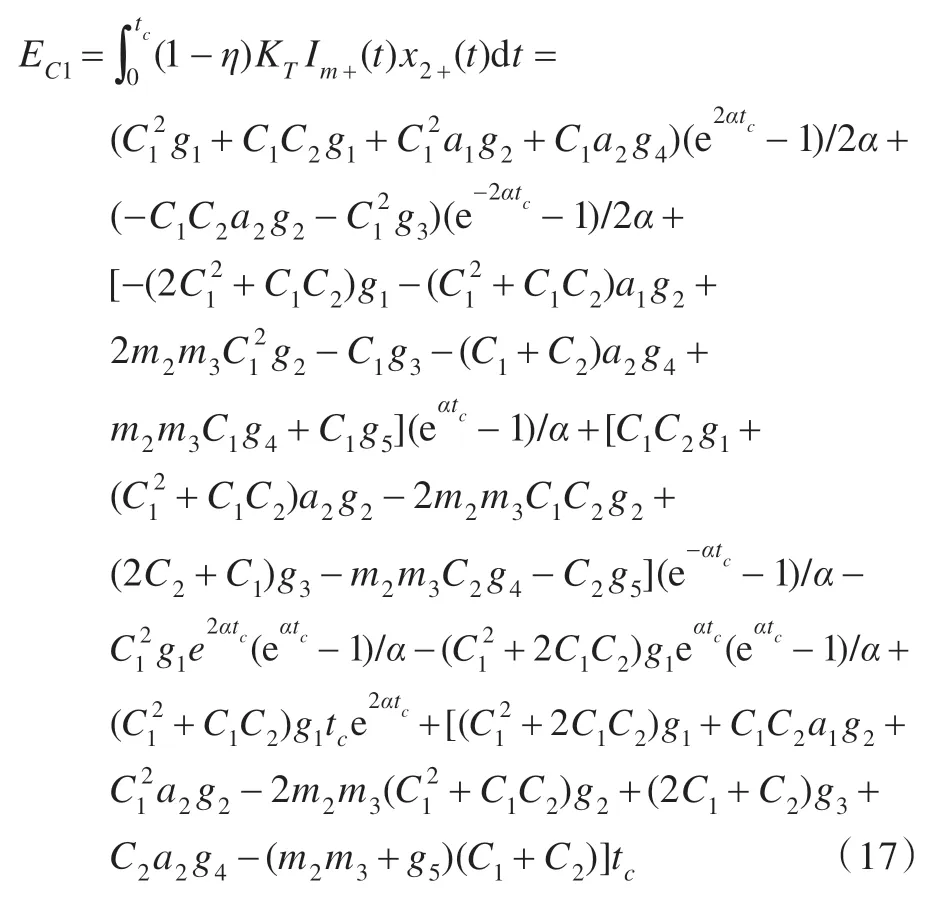
式（17）、（18）为加速阶段的库仑摩擦损耗，式（19）、（20）为减速阶段的库仑摩擦损耗。

粘性摩擦损耗EB计算如下：

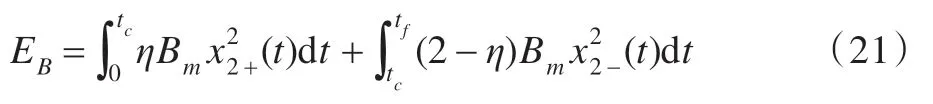
式（22）、（23）分别为加减速阶段的粘性摩擦损耗。负载损耗EL计算如下：

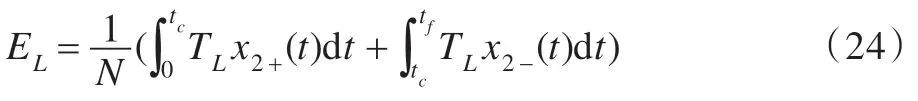
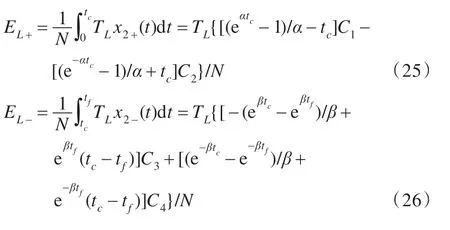
式（25）、（26）分别为加减速阶段的负载损耗。单个轮腿驱动系统的最小能量损耗为：

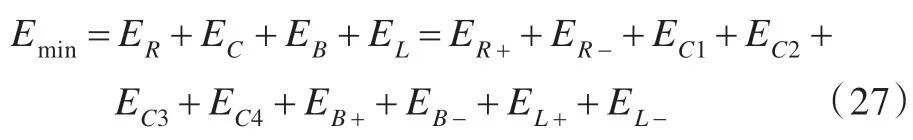
六足机器人的六条轮腿驱动系统的最小总能耗为：

式中EiR+、EiR-为第i条轮腿的焦耳热损耗；EiC1、EiC2、EiC3、EiC4为第i条轮腿的库仑摩擦损耗；EiB+、EiB-为第i条轮腿的粘性摩擦损耗；EiL+、EiL-为第i条轮腿的负载能耗。

驱动系统最小总能耗是关于加减速转换时间的函数。

3 最小能耗的影响因素分析

根据驱动系统的最小能耗模型，驱动系统的最小能耗受减速器的效率η、负载转矩TL、库仑摩擦力矩Tcm、粘性摩擦系数Bm等因素的影响。机器人每条轮腿运行在支撑相和摆动相时，采用点对点（PTP）控制模式，假设支撑相和摆动相的运行周期均为T，角位移为π。下面利用MATLAB 分析各因素对最小能耗的影响。驱动系统的电机选择maxon 公司生产的A-max32 直流电机+GS38A 型行星齿轮减速箱，参数如表1 所示。

表1 驱动系统参数

3.1 减速器效率对最小能耗的影响

图3为TL=4.35 Nm、Tcm=0.003 Nm、Bm=0.000 000 01、tf=0.4，减速器的效率分别为1、0.9、0.8、0.7 时的能量随加减速转换时间tc的变化曲线及能耗最小时刻局部放大图。驱动系统的最小能量消耗与最小能量消耗的加减速转换时间tc如表2 所示。矿井搜救探测机器人驱动系统最小能耗随减速器效率的减小而增大。加减速转换时间随着减速器效率的减小先减小后增大。

表2 不同效率下的最小能耗及转换时间

3.2 负载转矩对最小能耗的影响

图4为η=0.9、Tcm=0.003 Nm、Bm=0.000 000 01、tf=0.4，负载转矩分别为1 Nm、2 Nm、3 Nm、4 Nm 时的能量消耗随加减速转换时间tc的变化曲线及能耗最小时刻的局部放大图。驱动系统的最小能量消耗与最小能量消耗的加减速转换时间tc如表3 所示。矿井搜救探测机器人驱动系统最小能耗随负载的增大而增大。而加减速转换时间并不随着负载的变化而变化。

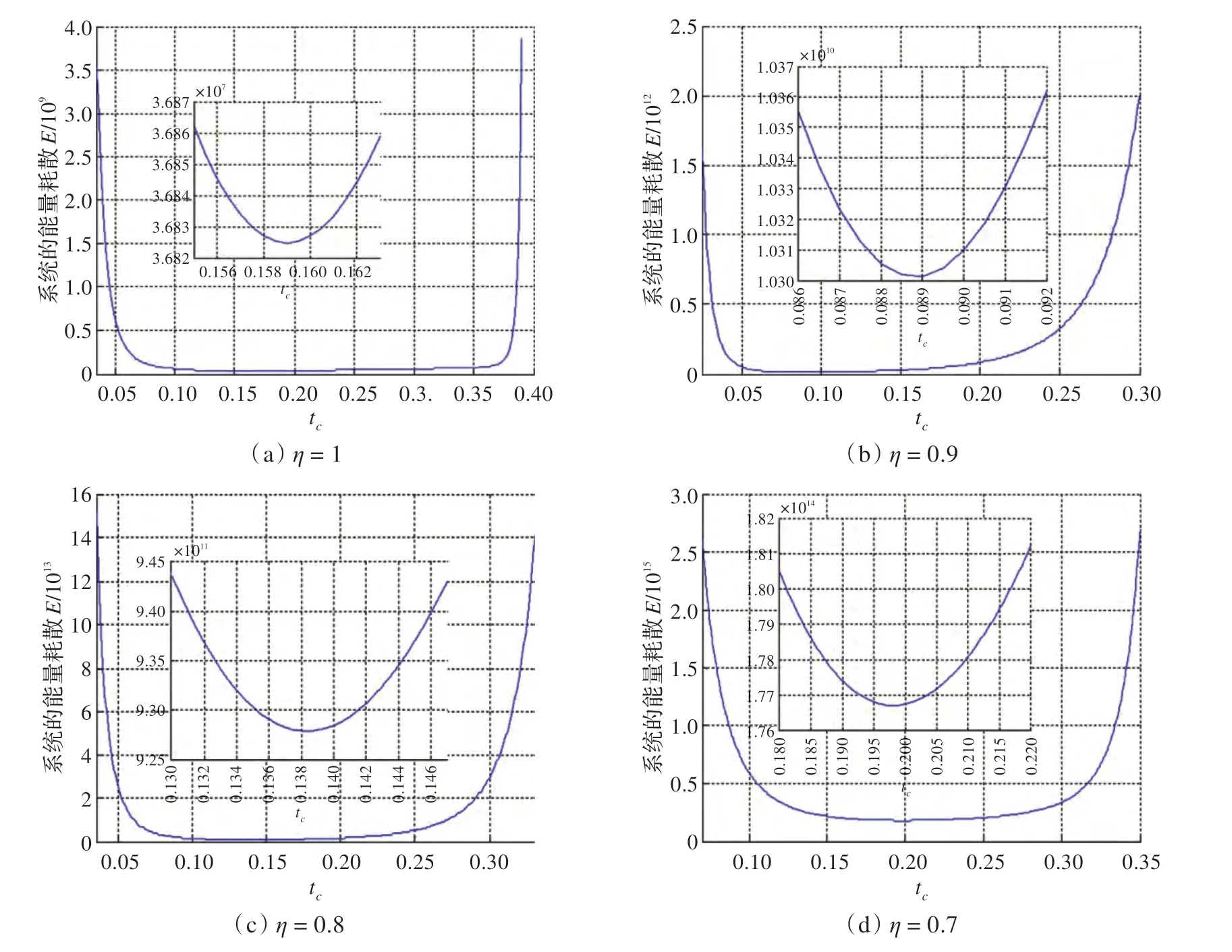
图3 不同效率的最小能量变化曲线

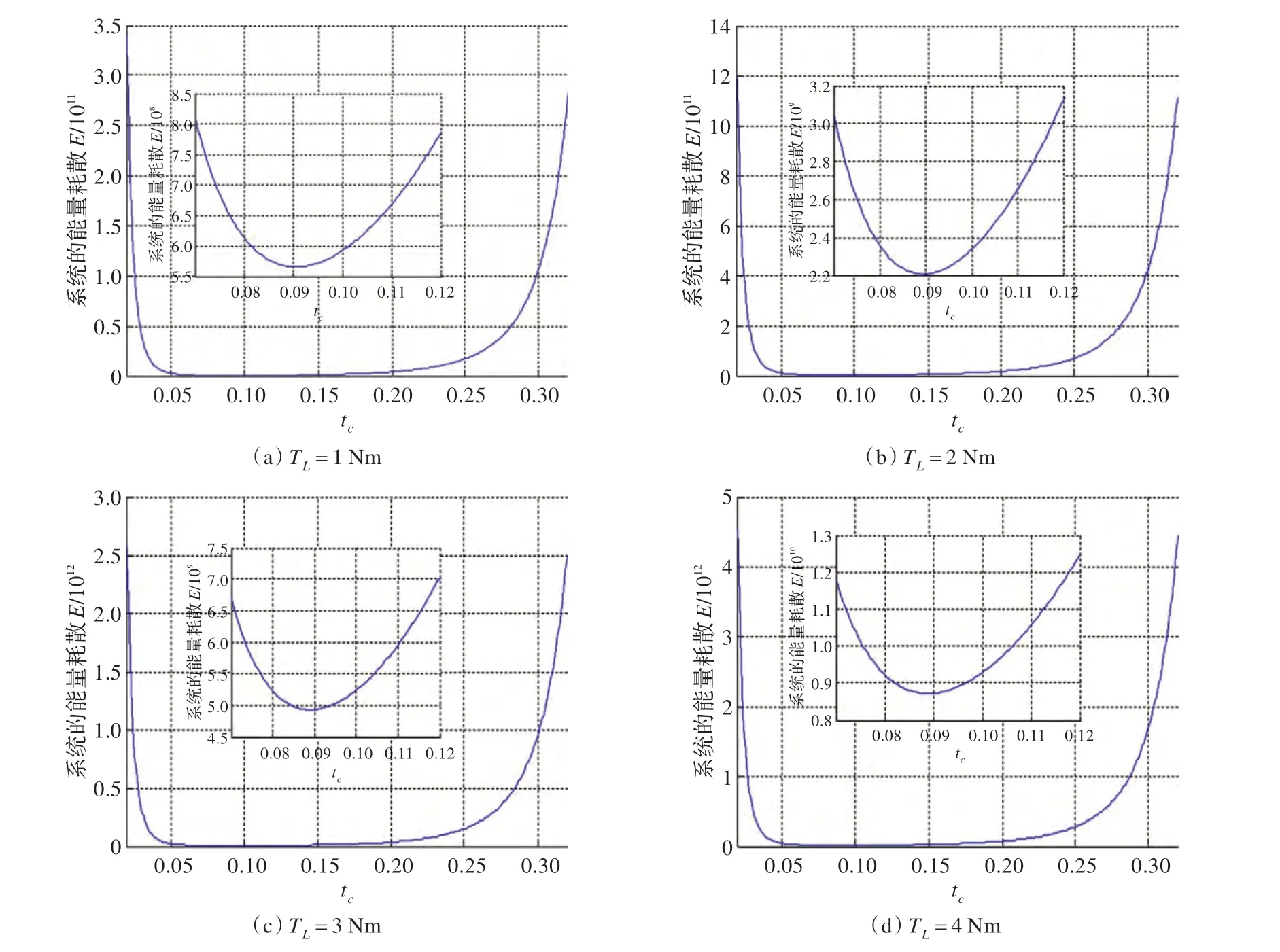
图4 不同负载的最小能量变化曲线

表3 不同负载的最小能量消耗及转换时间

3.3 库仑摩擦力矩对最小能耗的影响

图5为η=0.9、Bm=0.000 000 01、TL=3 Nm、tf=0.4，库仑摩擦力分别为0 Nm、0.001 Nm、0.01 Nm、0.1 Nm、1 Nm 时，驱动系统的最小能耗变化曲线及能耗最小时刻局部放大图。驱动系统的最小能量消耗与最小能量消耗的加减速转换时间tc如表4 所示。驱动系数的最小能耗受库仑摩擦力的影响较小，加减速转换时刻不受库仑摩擦力的影响。

3.4 粘性阻尼摩擦系数对最小能耗的影响

图6为η=0.9、TL=3 Nm、Tcm=0.003 Nm、tf=0.4，粘性阻尼摩擦系数分别为0.000 01、0.000 000 1、0.000 000 01、0.000 000 001 时，驱动系统的最小能耗变化曲线及能耗最小时刻的局部放大图。驱动系统的最小能量消耗与最小能量消耗的加减速转换时间tc如表5 所示。最小能耗随粘性摩擦系数的减小而增大，加减速转换时刻在提前。

4 结束语

本文根据矿井搜救机器人关节驱动系统的数学模型，利用Hamiltonian 函数和最小值理论，求解出了非线性摩擦条件下速度和控制电流，并建立了驱动系统的最小能耗模型。通过MATLAB 仿真分析，确定了减速器效率η、负载TL、库仑摩擦力Tcm和粘性摩擦系数Bm对驱动系统最小能耗的影响以及达到能量消耗最小的时间。为移动机器人驱动系统的参数优化配置提供理论上的支持，实现最小能耗的最优控制，对机器人节能降耗具有现实的重要意义。

表4 不同库仑摩擦力下的最小能耗及转换时间

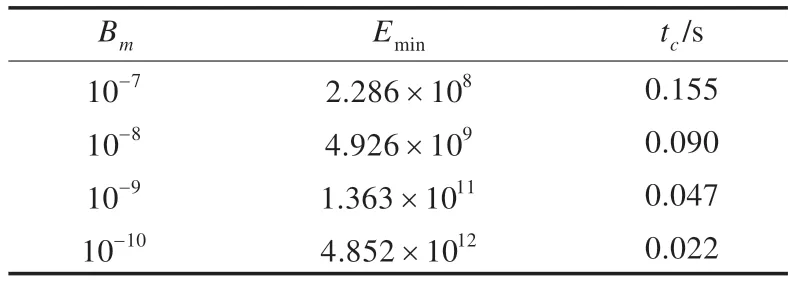
表5 不同粘性摩擦系数下最小能量及转换时间

图5 不同库仑摩擦力下的最小能量变化曲线

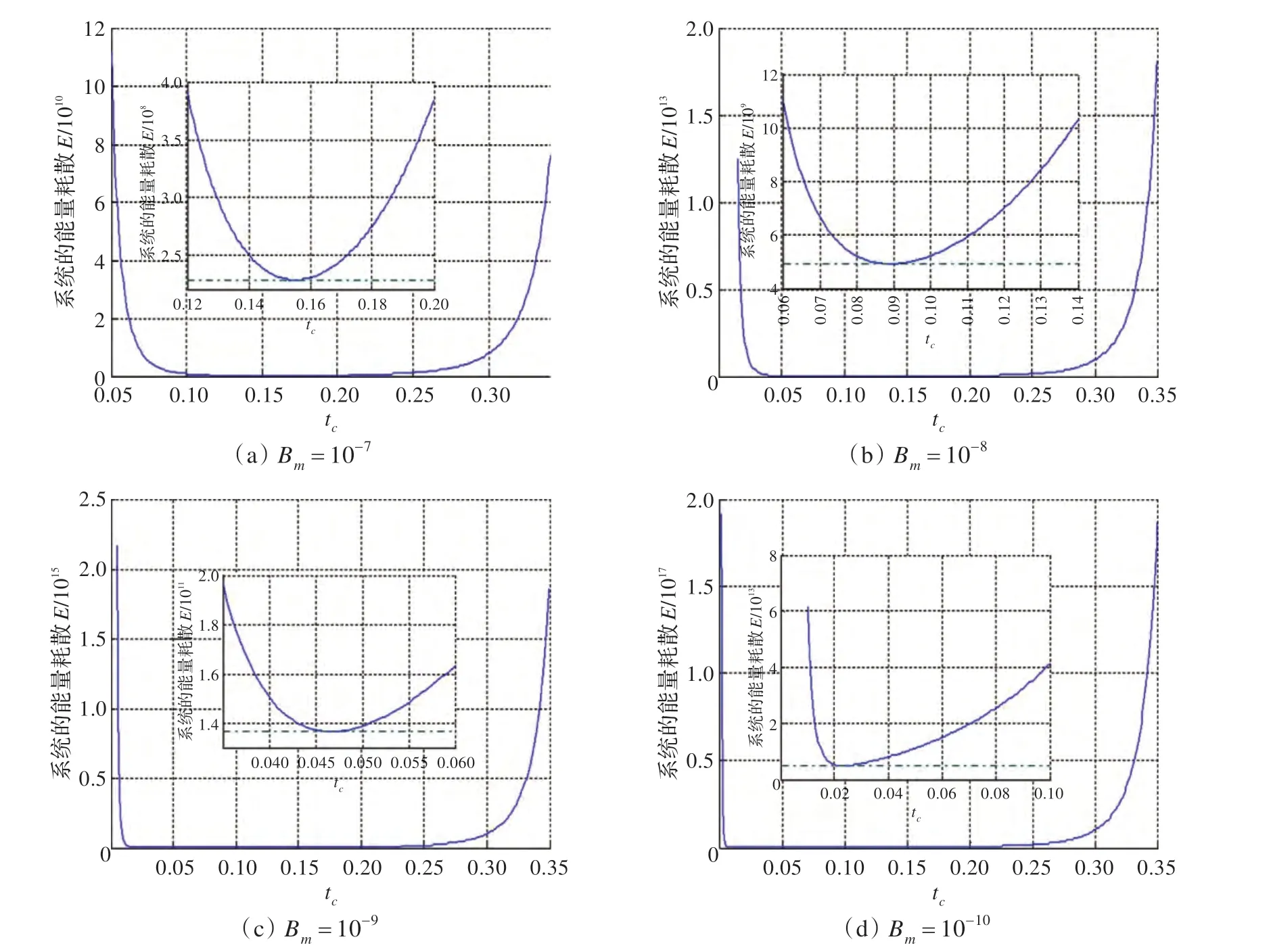
图6 不同粘性摩擦系数下驱动系统最小能量变化曲线

[1] 党培，谭云福，申利民.基于多关节机器人的能量最小消耗控制策略[J].计算机应用研究，2010，27（12）：4575-4577.

[2] 尹振娟.机械臂非线性摩擦最小能耗控制模型的研究[D].银川：宁夏大学，2013.

[3] Saramago S F P，Ceccarelli M.Effect of basic numerical parameters on a path planning of robots taking into account actuating energy[J].Mechanism and Machine Theory，2004，39（3）：247-260.

[4] Lee S，Park J，Haw C.Optimal control of a mackerelmimicking robot for energy efficient trajectory tracking[J].Journal of Bionic Engineering，2007，4（4）：209-215.

[5] Liu Shuang，Sun Dong.Optimal motion planning of a mobile robot with minimum energy consumption[C]//2011 IEEE/ASME International Conference on Advanced Intelligent Mechatronics（AIM2011），Budapest，Hungary，July 3-7，2011：43-48.

[6] Liu Shuang，Sun Dong.Modeling and experimental study for minimization of energy consumption of a mobile robot[C]//2012 IEEE/ASME Int Conf on Advanced Intelligent Mechatronics，Kaohsiung，Taiwan，July 11-14，2012：708-713.

[7] 孙敏，范守文.基于能耗指标的拟人机器人步态优化与分析[J].机械设计与研究，2007，23（4）：52-55.

[8] 霍炜，刘大维.基于局部最小能量的移动机器人路径规划[J].青岛理工大学学报，2008，29（4）：99-103.

[9] 金波，陈诚，李伟.基于能耗优化的六足步行机器人力矩分配[J].浙江大学学报：工学版，2012，46（7）：1168-1174.

[10] Roy S S，Pratihar D K.Dynamic modeling and energy consumption analysis of crab walking of a six-legged robot[C]//2011 IEEE Conference on Technologies for Practical Robot Applications（TePRA），IEEE，2011：82-87.

[11] Kar D C，Kurien Issac K，Jayarajan K.Minimum energy force distribution for a walking robot[J].Journal of Robotic Systems，2001，18（2）：47-54.

[12] 徐海黎，解祥荣，庄健，等.工业机器人的最优时间与最优能量轨迹规划[J].机械工程学报，2010（9）：19-25.

[13] 李智国，李萍萍，刘继展，等.不同加减速控制算法的能耗分析与比较[J].农业机械学报，2009（8）：193-197.

[14] 丛爽，李泽湘.实用运动控制技术[M].北京：电子工业出版社，2006.

[15] 黄平编.最优化理论与方法[M].北京：清华大学出版社，2009.