基于AMESim的高压气动减压阀的稳定特性

， 　， ， (兰州理工大学 能源与动力工程学院, 甘肃 兰州　730050)

引言

随着雾霾天气影响不断加重，石化燃料消耗量日益增加，在环境恶化和经济发展的双重压力下，氢能源作为一种理想的新的合能体能源，以其特有的性质越来越受到人们的重视。随着汽车行业、氢能源汽车逐步发展，高压气动减压阀是气动汽车中氢气输运系统中重要的控制元件。为保证燃料电池所需的工作压力的恒定，经过减压阀后的输出压力值应不会随着流量和输入压力的变化而变化[1]。但由于依靠节流实现减压的气动减压阀，在减压过程中势会有较大的能量损失，而气动汽车所携带的能量是有限的，能量的损失将会降低系统的利用率。基于此高压气动减压阀既快速又稳定减压，使能量损失较少就成为了关键问题[2]。

本研究选择一种带有先导稳定流量器的高压气动减压阀，采用AMESim 软件对其进行建模仿真，研究其压力和流量控制特性[3]，是否满足氢能源汽车输气控制的要求。

1　高压气动减压阀结构及原理

1.1　高压气动减压阀结构

图1所示,先导式高压气动定压比例减压阀，其结构为主阀口常闭型减压阀，主要由主阀、先导阀、控制器、比例电磁铁等组成。先导阀采用锥阀结构，主阀采用具有锥阀和滑阀的结构形式。当B口没有压力时，调节弹簧9使主阀芯组件处于进口A和出口B断开状态，当高压气体先经过进口A和先导流量稳定器，进入主阀弹簧腔，再通过阻尼口8进入主阀下腔，上、下腔形成压差，将主阀打开后，减压原理同常开型一致。

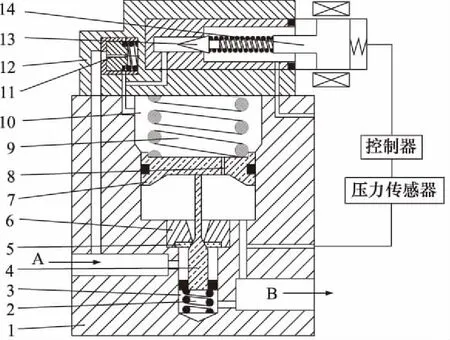
1.主阀体　2.复位弹簧　3.反馈腔　4.主阀芯　5.密封挡圈 6.主阀座　7.活塞　8.阻尼口　9.调节弹簧　10.调压腔 11.先导流量稳定器　12.先导阀体　13.先导阀芯　14.比例电磁铁

1.2　气动减压阀中先导流量稳定器

如图2，先导流量稳定器由两个气阻构成，活塞上细长孔R0为固定气阻，轴向移动的活塞与阀套后部径向小孔构成可变气阻R1。可以看出，先导流量稳定器实际上是按气动B型半桥原理工作。当进口压力pA升高时，活塞左右原有的气压力与弹簧力的平衡被破坏，气压力的升高推动阀芯向右移动，阀套上径向小孔被活塞挡住一部分，使孔开度关小，可变气阻R1增大。由于阀芯向右移动，内腔体积变小，压力pR增大，固定气阻R0前后的压差pA-pR保持不变，使的流过固定气阻R0与可变气阻R1的流量保持基本不变，当pA减小时，pR也减小，R0前后压差与流过流量也基本保持不变。因此，在进口压力波动的情况下先导流量稳定器很好地保持先导阀进气腔和主阀调压腔的流量稳定。

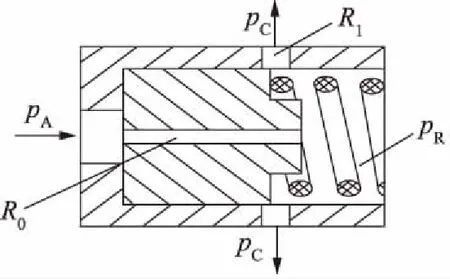
图2　先导流量稳定器

2　高压气动减压阀数学模型分析

AMESim软件平台中的物理模型参数的调整与设置需基于模型对象底层的数学模型，对高压气动减压阀仿真之前，首先需要分析高压气动减压阀的数学模型，在此基础上进行物理模型搭建，可以合理高效地设置模型参数，对物理模型进行优化及故障分析与检测。本节将对高压气动减压阀的核心部件及概念进行数学模型分析。

2.1　模型的假设条件

为方便模型的建立和简化，作如下假设：

(1) 气体通过高压气动减压阀的阀口可看作一个等效的收缩喷嘴来计算；

(2) 气体在各阀口或节流通道中的流动为绝热流动；

(3) 气源温度为环境温度T=293 K；

(4) 不计密封比压及密封不良造成的气体泄漏；

(5) 不考虑重力场的影响。

2.2　高压气动减压阀主阀模型

先导式减压阀基于流量连续性方程和力学平衡方程。氢气具有可压缩性，工作过程中在减压阀的各个容腔中会发生体积的改变[4]。为了简化计算，将气动技术中气流通过的气动回路(气动元件和连接元件的气管组成)经过的管道系统等效成收缩喷嘴或节流小孔来计算，在根据具体的要求修正各个参数。因此，气体在各个阀口的流动可视为经过收缩喷管流动，流量方程为[5,6]：

(1)

式中：

式中：κ为气体绝热指数，氢气κ为1.4；Cd流量系数；T为系统温度(K)；S为阀口节流面积(m2)；pu、pd为前、后腔压力(Pa)。

1) 主阀口流量方程

根据式(1)，可得到：

(2)

2) 主阀阀芯动态力平衡方程为：

(3)

式中：Ff1为主阀芯受到的摩擦力；Ffl为气体流动作用力；pB、pt分别为减压阀输出压力值、调压腔压力值；m1为主阀阀芯的质量；x为主阀阀芯位移；β1为主阀阀芯的阻尼比；K1、K2为主阀预紧弹簧、主阀复位弹簧刚度；x01、x02为主阀预紧弹簧、复位弹簧预压缩量；A1、A2、A3为活塞在出口腔侧、调压腔及复位弹簧腔气体压力的作用面积。

2.3　先导稳定流量器模型

从主阀引出的气流通过细长孔到先导稳定流量器，即气体从A腔流向先导稳定流量器弹簧腔的流量记为q先，在细长管中的流动为层流，其质量流量为：

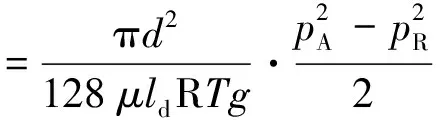
(4)

式中：μ为气体的黏度(Pa·s)；d为细长孔的直径(m)；g为重力加速度(m/s2)；ld为细长孔的长度(m)。

2.4　高压气动减压阀先导阀模型

先导阀芯动态力平衡方程为：

pcA4-pBA3-Ff2-Ffl

(5)

式中：Ff2为先导阀芯受到的摩擦力；Ffl为气体流动作用力；Fe比例电磁铁输出的推力；pc为先导流量稳定器输出的压力值；m2为主阀阀芯质量；y为先导阀阀芯的位移；β2为先导阀阀芯的阻尼比；K3为先导阀复位弹簧刚度；y0为先导阀复位弹簧预压缩量；A3为复位弹簧腔气体压力的作用面积；Ay、A4为先导阀出气腔、进气腔中气体压力对阀芯的作用面积。

3　高压气动减压阀仿真模型

3.1　建立仿真模型

带先导流量稳定器的比例减压阀模型，见图3。

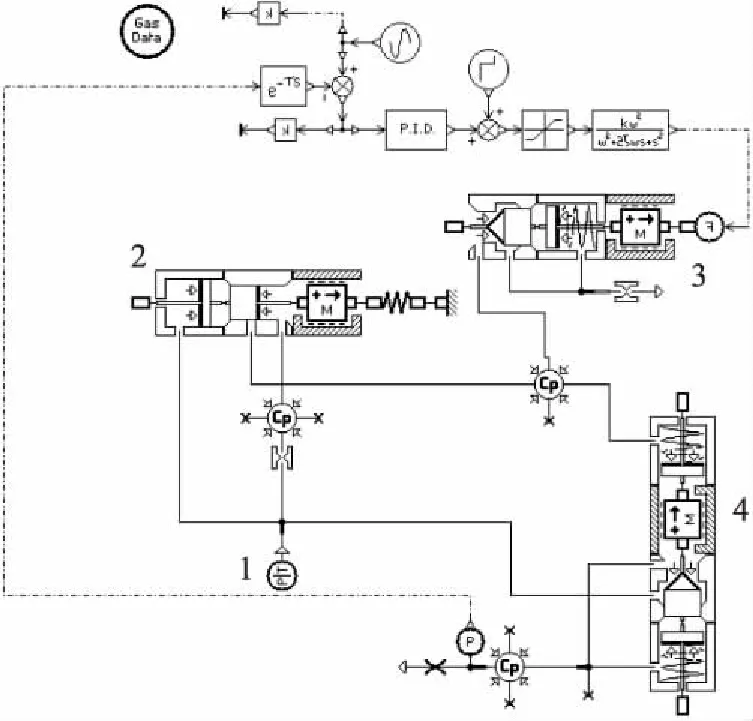
1.压力气源　2.先导流量稳定器　3.先导阀　4.主阀

3.2　设置仿真模型参数

仿真模型中主要的参数设置如下：气体介质为氢气，气态氢密度为0.0899 g/L。压力出口设定压力为5 MPa;先导阀控制电流600 mA,先导阀芯质量为0.073 kg,先导阀芯直径为4.2 mm;先导流量稳定器最大位移为10 mm, 先导流量稳定器弹簧刚度3.8 N/mm；主阀调节弹簧刚度为25 N/mm；主阀阀芯质量为0.1 kg。

4　仿真结果分析

4.1　减压阀静态特性

图4为减压阀压力特性曲线，由曲线可知：输入减压阀的压力在0～35 MPa范围内变化，输出压力对输入压力的响应尽管出现振荡，但很快就会稳定于期望值上(5 MPa),即高压气动减压阀的响应具有收敛的性质。

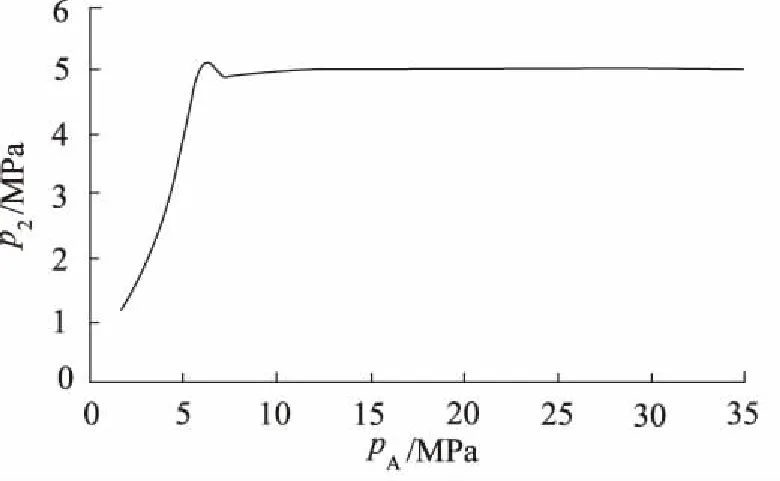
图4　减压阀压力特性

图5为流量特性曲线，由图得出：随着减压阀主流量的增加，减压压力逐渐下降，但下降幅度极小，具有良好的负载能力。

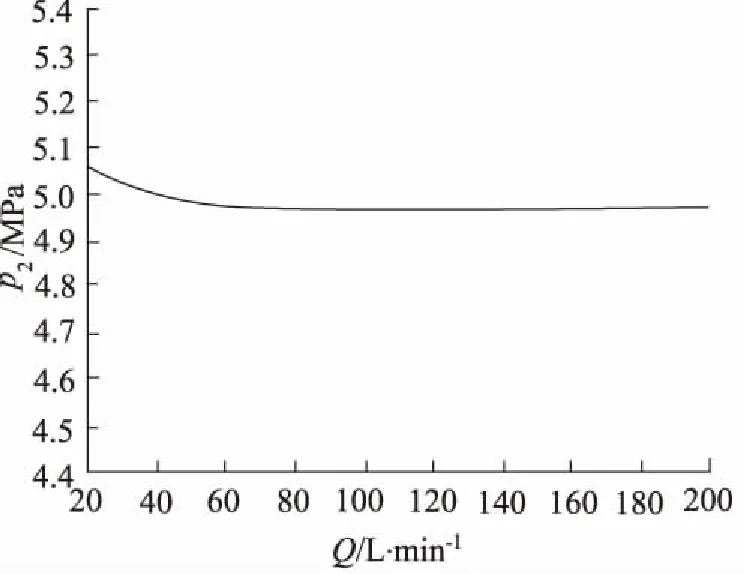
图5　减压阀流量特性

由图6分析可知：曲线1为带先导稳定流量器的比例减压阀，超调量为10%。曲线2为传统先导比例减压阀，超调量达到20%；对比表明：带先导稳定流量器的比例减压阀其超调量小，振荡衰减快，即带先导稳定流量器的比例减压阀稳定性与快速性更好。

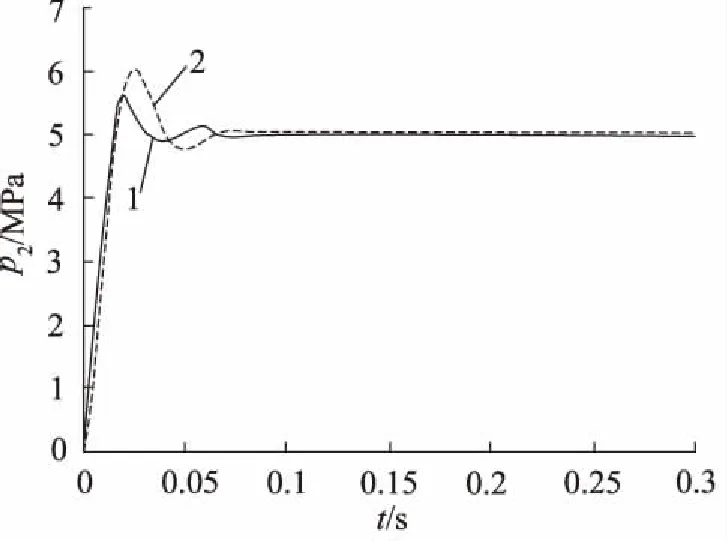
图6　带先导稳定流量器型与传统型先导减压阀

4.2　 主要参数对输出稳定性影响分析

1) 先导阀弹簧弹簧刚度的影响

如图7所示，保持其他参数不变，先导阀弹簧刚度不同情况下，对减压阀输出压力的影响。弹簧的刚度分别设置为15 N/mm、20 N/mm、25 N/mm。

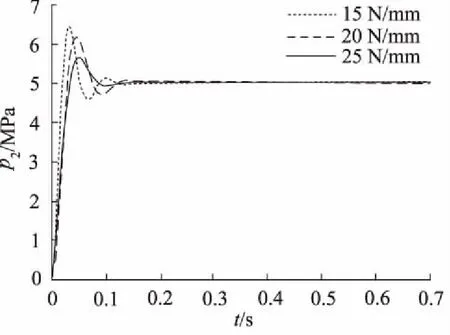
图7　先导阀复位弹簧刚度对减压阀输出压力影响

由图7仿真结果表明：当弹簧刚度增加时，减压阀出口压力波动幅度减小，稳定性好，在短时间内达到稳定的压力输出。反之，随着弹簧刚度的减小，阀出口波动幅度变大，频率变高，在较大的出口压力波动的影响下，到达平衡位置的时间变长。

2) 先导流量稳定器的活塞阻尼孔直径的影响

图8为不同先导流量稳定器的活塞阻尼孔直径的情况下，对减压阀输出压力影响曲线。活塞阻尼孔直径分别设置为0.2 mm、0.4 mm、0.8 mm。

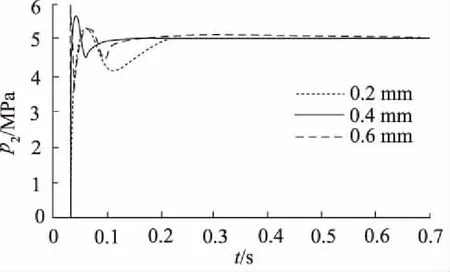
图8　活塞阻尼孔直径对输出压力影响

由图8的仿真结果表明：随着先导流量稳定器的活塞阻尼孔直径增大，减压阀输出稳定压力为5 MPa不变；但其开启时,随着活塞阻尼孔直径增大，压力振荡越大，稳定时间增大，动态响应变慢；当活塞阻尼孔直径为0.2 mm时在0.2 s以后才可稳定；直径为0.4 mm 时在0.1 s就可达到稳定；当活塞阻尼孔直径为0.8 mm时，虽动态响应快，但输出压力的稳定性差。

3) 主阀复位弹簧弹簧刚度的影响

如图9保证其他的参数不变，主阀的复位弹簧刚度不同情况下，对减压阀输出压力的影响。弹簧的刚度分别设置为35 N/mm、40 N/mm、45 N/mm。

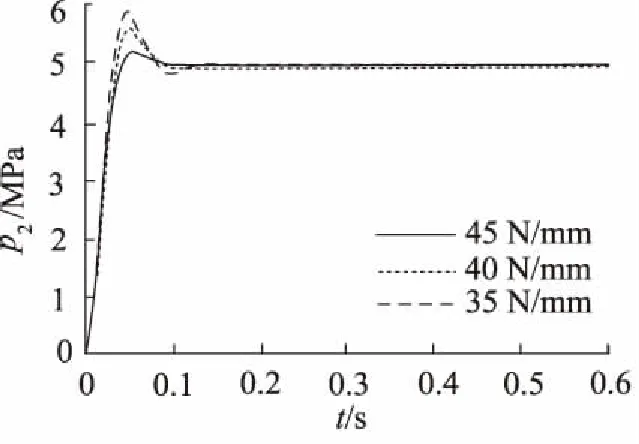
图9　主阀复位弹簧刚度对减压阀输出压力的影响

由图9仿真结果表明：当弹簧刚度小时，输出压力超调量大；随着刚度增加时，减压阀输出压力的稳定性也在变强，压力颤动的振幅变小，且到达稳定状态所需的时间也减少，但增大弹簧的刚度会增大阀的尺寸。

4) 出口腔的容积变化对减压阀动态响应影响

图10为出口腔的容积变化对减压阀动态响应的影响曲线。仿真中的出口腔体积分别为设计值的200%、100%和50%。

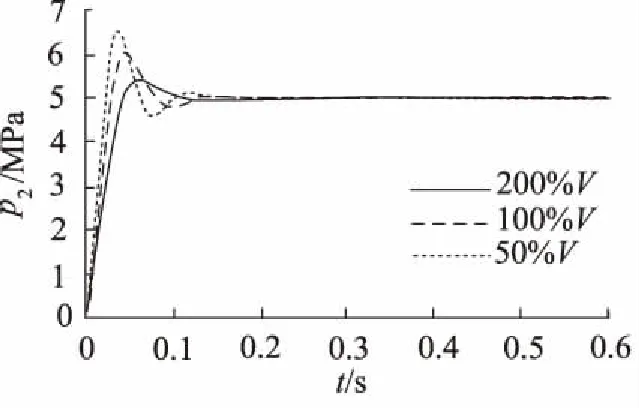
图10　主阀不同出口容积对输出压力影响

由图10仿真曲线表明：随着出口容积变小，气体在阀口处急剧收缩，然后开始释放，所以出口体积过小会影响气体的释放，会造成很大的压力波动；因此适当增大出口腔容积是很有必要的。经过阀口的高速气体在较大的出口容腔中能够缓慢释放，能够有效降低压力梯度，减小压力波动，表现在曲线上为震荡幅值和超调量相对较小。

5　结论

(1) 用AMESim软件对高压气动减压阀进行仿真，通过合理的建模与参数设置，可知带有先导稳定流量器的高压气动减压阀在高压化减压时，其出口压力稳定、压力振荡小、动态响应快；能够有效地抑制出口的压力波动；

(2) 在设计先导式高压气动减压阀时，采用基于气动半桥原理的先导稳定流量器结构；同时，适当地增大主阀复位弹簧刚度，先导稳定流量器活塞阻尼孔，出口腔容积的增大，可提高阀的输出压力的稳定性和快速性。

参考文献：

[1]李宝仁,杨刚,杜经民.高压随动压力控制阀动态性能的仿真研究[J].华中理工大报,1998,26(7):24-26.

[2]刘祖前.超高压气动减压阀的研究[J].机床与液压，1999，(3):62-63.

[3]王飞. 基于AMESim的流量-压力复合阀静特性研究[J]. 液压气动与密封，2009,(6):20-22.

[4]李建藩.气压传动系统动力学[M].广州：华南理工大学出版社,1991.

[5]魏东,孙启顺,谢华.一种新型小流量、高压差减压阀的研制[J].液压与气动，2002,(11):51.

[6]Massimo Sorli, Giorgio Figliolini, Stefano Pastorelli. Dyanmic Model and Experimental Investigation of a Pneumatic Proportional Pressure Valve[J].IEEE/ASME Transactions on Mechatronics,2004,9(1):78-85.