基于形态学和距离变换的根系图像交叉的分离

石 锐，刘 辉，朱 鑫，刘晶淼，贾庆宇

1.重庆大学 计算机学院，重庆 400044

2.中国气象局 沈阳大气环境研究所，沈阳 110016

1 引言

环境因素对于植物的生长有着很大的影响，根系形态是反映植物生长状况的重要特征，因此研究植物根系形态对于研究环境因素对植物生长的影响具有重大意义。对于根系的研究，文献[1]采用由人工取根、洗根、称重的方法，不仅浪费时间、人力和物力，而且易造成根部损坏，精确度不高。随着数字图像技术的发展，人们已经开始将数字图像处理技术应用在根系形态的研究中，并且取得了一定成果。

为获取根系的形态参数，研究者需要对每条根及分支进行相应参数计算，但是在该项目研究的根系图像中存在大量根系杂乱交错的现象。因此要获得精确的根部动态生长的形态参数，须对图像中交叉的根、主根和侧根进行分离。在分离交叉物体的研究中，虽然已经有些方法取得了一定成果，比如粘连细胞的分离[2]，人们利用分水岭算法、距离变换等方法实现了细胞的分离，其中，分水岭算法用于分割圆形或者类圆形结构的重叠、粘连目标效果不错，但是对于树根这种宽度不均匀且形状弯曲不定的目标，就无能为力了。此外也有人研究过交叉纤维的分离，余承健[3]提出的分离方法过程繁琐，只检测交叉部分，无法解决根系分叉的情况，孟荣爱等[4]提出了一种新型方法，也只能分离只有一个交叉点的物体，而且效率不高。

本文在前人研究的基础上，针对根系图像的形态特征，将形态学和距离变换相结合提出一种新的有效的分离方法，大量实现证明，既避免了分水岭算法的过分割现象，也在精确度和效率上得到了提高。

2 根系图像的获取及预处理

项目中图像的获取是通过使用接触式图像传感器（CIS）将其置入插进土壤的透明玻璃管中，通过操作CIS设备即可得到沿玻璃管壁一周的根部图像（如图1，根据项目需求图像分辨率为600 dpi，实际图像大小为4 100像素×415像素，为方便展示截取500像素×415像素大小进行分析）。由图中可见，曝光度不均匀造成了背景土壤颗粒的干扰和其他噪声，鉴于图像的分离需要在二值化的轮廓清晰的根系图上进行，因此需要对图像进行根系分割。

对根系原图像进行全局阈值二值化处理，利用OTSU分割技术[5]将完整根系和沙粒、土壤等背景分离，辅以人工交互处理图像已达到更好的效果，如图1（b）和（d）分别为得到的图（a）和（c）根系二值图。

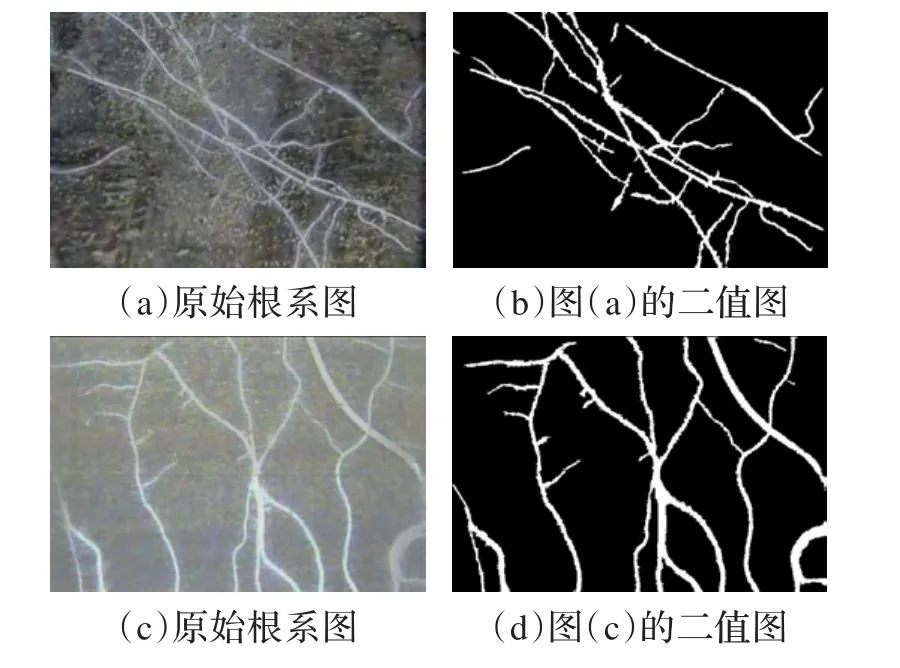
图1 原始的根系图及其二值图（分辨率为200 dpi）

3 交叉分离过程

3.1 算法原理分析

首先给出几个概念：

（1）抑制

图像中一个目标被另一个目标覆盖的现象，这里的“一个目标”称为被抑制对象，“另一个目标”称为抑制元素，用数学逻辑表示该运算如下：

1Δ 0→1，1Δ 1→0，0Δ 1→0，0 Δ 0→0

其中，1代表目标像素值，0代表背景像素值，Δ代表抑制运算。

（2）影响区骨架

给定一个连通成分，影响区[6]定义为二值图像中比其他连通成分更接近于给定连通成分的像素点集。因此，在二值图像的连通集及其影响区之间存在一一对应关系，影响区的边界定义为影响区骨架。假定X表示二值图像或图像平面的像素集合，K1，K2，…，Kn为X的连通成分，则

连通成分Ki的影响区IZ是图像平面像素中比X中其他连通成分更接近的像素点集：

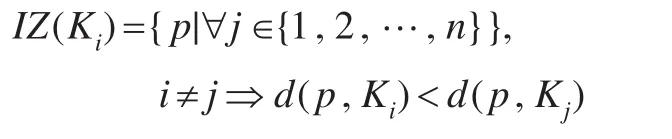
实际应用中，二值图像的影响区IZ通常被当做标记图像使用，每个标记区域对应于输入二值图像连通成分的影响区。

影响区骨架或SKIZ定义为不属于任何影响区的点集：

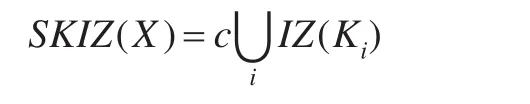
影响区骨架等价于影响区边界。

为了分离交叉的根系，可以考虑查找根系边缘图的交叉点，然后在交叉点之间进行连线，即可分离交叉的根系。根据交叉区域的交叉方式不同，连线方式可分为：一种是图2（a）中的邻接交叉，仅有两个点，用一条线段连接起来即可；另一种是图2（b）中的相互交叉，四个点可以相邻连接，也可以对角连接。至此，要解决的就是配对问题，即判断哪两个点或者四个点属于同一个交叉区域，余承健提出了该问题的解决方法，但是该方法的精确度不高，且效果不佳，存在很多后续问题。

图2 连线方式

如果换一种思路，假设根系已经完成分离，此时成为假分离，那么图中每一个连通区域都是一条没有分叉或交叉的独立的根，根据影响区骨架（欧式距离变换）的意义，每条根都有一个影响区，且所有的影响区构成了整个图像，此时成为影响区图像，该图像的骨架也是分离影响区的边缘，更是分离交叉根的边缘。因此，如果得到根系的假分离图或者近似假分离图，问题就迎刃而解了。

图像的骨架是简化原始图像目标的信息，但是保留了原目标的同伦结构。鉴于此，将根系的骨架图像的假分离图像作为上述提到的假分离图有异曲同工之妙。接下来就是分离交叉处，考虑到非单一像素的目标交叉骨架化后并不止交叉于一个点，如图2（c）所示，另外由形态学的膨胀运算可知，两个近距离的目标通过一定程度的膨胀会连接在一起，成为一个目标。因此，可以将骨架交叉点作为单独的目标，设计合适的结构元素进行膨胀，使相近的交叉点连接在一起，从而得出真实的交叉点。然后采用上述的概念定义1，除去骨架图中交叉部分，得到分离的骨架图。此时分离的骨架图与上述提到的假分离图中，各个连通分量是一一对应的，因此可以利用距离变换完成交叉根系的分离。

3.2 算法过程描述

算法流程如图3所示。

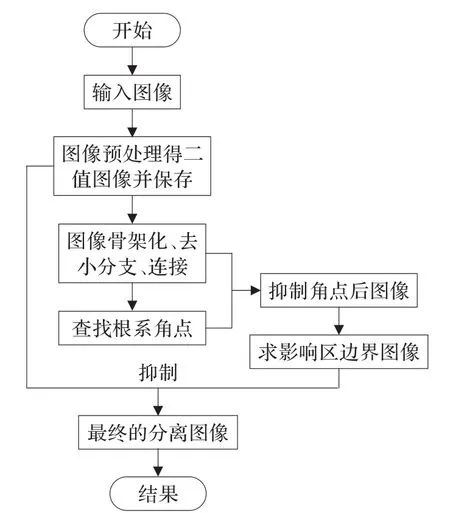
图3 分离算法流程图

具体步骤如下：

步骤1预处理。为了减小图像凹凸不平的边缘和根系内部的空洞对分离效果的影响，需要做图像高斯平滑和孔洞填充操作。

步骤2根系图像骨架化。通过对比文献[7]中提到的基于形态学的击中击不中算法和中轴变换方法的实验效果，选定中轴变换进行根系图像骨架化，获得连续的单像素骨架图。

步骤3求交叉点。对骨架图进行扫描，采用文献[8]中改进的交叉点搜索方法求得交叉点。

步骤4选用半径为3的圆盘结构对交叉点进行膨胀，将骨架化中的交叉部分抑制，得到分离的根系骨架图。

步骤5对抑制后的图像求影响区边界。该步骤采用基于欧式距离变换[9-10]标记的方法实现。欧式距离变换是计算并标识空间点（对目标点）距离的过程，将二值图像转换为灰度值为欧式距离的灰度图，本文也是通过计算背景点对每个已标记的连通域的距离，但是标记方法不同，将背景中距离连通域i比其他所有连通域近的点集P(i)定义为属于连通域i，对P(i)中的所有点标记灰度值i，此时的标记图像被分成了N块（假设有N个连通区域），最后采用自适应双阈值，以及对边缘敏感的Canny算子[11]求出该标记图像的边缘，便是影响区边界。

其中，欧氏距离变换是基于一种线性时间的算法[12]实现的。算法将一幅二值图像看作一个二维矩阵，先以矩阵的列为单位，求出每列中距离每个背景点最近的目标点并记录在Sd中，然后以行为单位，针对每行的所有背景点，按照逐步构造Voronoi图[13]的方法求出距离每个背景点最近的目标点。在构造第d行的Voronoi图时，采用两层循环实现，外层循环从Sd中取出属于背景点i的目标点Fv，内层循环判断并去掉不可分割行d的Fv，其中判断条件为，假设u、v、w是三个目标点，满足条件ud＜vd＜wd，uv的中垂线与vw的中垂线分别与行d交于点x、y，若x的纵坐标大于y的纵坐标，则v点不能分割行d。

步骤6对原二值图像与影响区边界做抑制，分离完成。

4 实验结果与分析

根系交叉分离的实验是在Windows XP操作系统，MATLAB R2012a的软件环境下进行的，采用30张植物根系的图片作为实验数据，现仅选取原根部图像（a）和图像（b）的部分根系进行实验结果展示。

以图1（b）中截取的部分根系图4为例，首先求出其骨架，查找交叉点并膨胀，不同幅度的膨胀得到的分离根不同。如图5中四幅图片分别为膨胀次数pz为2、4、6、9得到的结果，可知随着膨胀次数的增加，交叉处多个交叉点合并，但是也不可避免地造成了相邻根的断裂。因此选择合适的膨胀次数，既能保证交叉处完全分离，又能保证原根的连接性，后续的实验选用膨胀次数为6进行。

图4 交叉的根系及其骨架化

图5 膨胀次数分别为2、4、6、9的结果图

其次采用距离变换标记得到影响区边界，如图6，图中的每一个封闭的区域代表每条根所在的影响区；最后的分离图为图7。

图6 影响区骨架

图7 分离的根系

为进一步说明本文算法的效果，本文还采用几种不同的算法对图像中的部分根系进行分离和比较，如图8。

图8 不同算法对图像的部分根系进行分离比较

图8中，（a）、（e）作为分离图像；效果图（c）、（g）采用的是由Srisang等人[14]提出的基于几何学的算法进行分离，可以看出图（c）基本没有分离，图（g）只分离了互相交叉的部分，分支处没有分离。该方法只分离有四个交叉点的物体，不适用于分叉过多的根系图像。

另外一种分离方法是由Madian等人[15]提出的利用图像轮廓的兴趣点建立假设的方法，假设分离线的端点在空间上的距离小于其沿轮廓产生的长度，得到的效果图为图8（d）、（h）。由图可见，其分离效果和本文算法的效果相差不大。这种方法需要对图像的各个兴趣点的所有组合对求其沿轮廓的距离，算法复杂性太高，尤其对于拓扑性很强的根系网，所需存储空间大。

根据项目要求，提出的算法可以实现在交叉部分和根的分支完成分离，得到单独的根段，完成分割。根系分离的标准定义为：对二值图像骨架化，求得每一个分叉点的分叉数之和numofbranch和端点数numofend，理想情况下得到的根段数为：

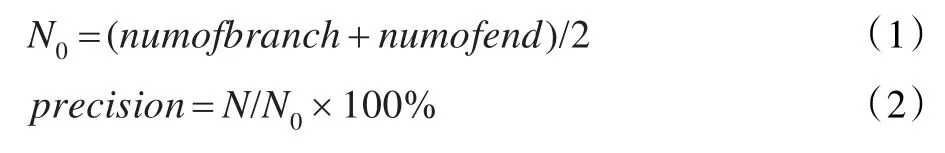
式（2）为分离准确率的计算方法，当precision＞1则说明过分离，precision越接近1说明算法精度越高。

针对同一大小（500像素×415像素），相同形状特征的根系图像，根据以上计算方法得到本文算法与其他算法分离结果的对比，如表1。

表1 几种算法分离效果对比

由表1可知，本文提出的算法准确率能达到94.1%，和基于假设的算法不相上下，但是运行速度快了15.865倍；基于几何学的算法与本文算法在运行时间上差不多，但是它不能分离主根和侧根相接的情况而这种情况又是占大多数，因此分离效果不好。

5 结束语

本文算法仍存在一些不足需要改进：算法是对整张图片进行操作，没有考虑图像中存在不用参与分离的孤立的根段，这会增加处理过程的复杂度，在以后的工作中可以考虑先将图像中单独的根段先分离，提高算法执行效率。另外，交叉点膨胀的幅度需要人为控制，不适于图9（a）中的根系过于粗而分叉又过细的图像，否则容易产生图9（b）的这种块状，需要在以后的工作中进行改进。

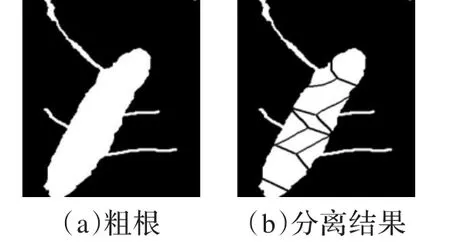
图9 粗根的分离结果

针对交叉根系图像，在原有的交叉重叠物体分离方法的基础上，提出基于形态学和距离标记变换结合的算法，充分利用了形态学的膨胀运算和距离变换的标记思想，将根系在交叉处进行分离。通过以上实验验证，本文算法能够快速准确地实现交叉根系的分离，为根系图像的形态参数分析和计算提供有效的方法策略。由于根系的特殊形态，该算法还可以广泛应用在条状物体的交叉分离操作中。

[1]Pearcy R，Ehleringer J，Mooney H，et al.Plant physiological ecology[M].New York：Chapman and Hall，1989：1-9.

[2]游迎荣，范影乐，庞全.基于距离变换的粘连细胞分割方法[J].计算机工程与应用，2005，41（20）：206-208.

[3]余承健.纤维检测中交叉图像的分离方法[J].电脑知识与技术，2006（7）.

[4]孟荣爱，周长剑，邱书波.纸浆纤维交叉分离的一种新型算法[J].纸和造纸，2011，30（8）：67-70.

[5]胡敏，李梅，汪荣贵.改进的Otsu算法在图像分割中的应用[J].电子测量与仪器学报，2010，24（5）：443-449.

[6]Soille P，王小鹏.形态学图像分析原理与应用[M].2版.北京：清华大学出版社，2008：125-127.

[7]江萍，徐晓冰，方敏.基于形态学骨架提取算法的研究及其实现[J].计算机应用，2003，23（S1）：136-137.

[8]张华，叶海建，王彦，等.改进的二值图像的交叉点扫描检测算法[J].自动化技术与应用，2009，28（3）：48-49.

[9]阮秋琦，阮宇智.数字图像处理[M].2版.北京：电子工业出版社，2004：51-54.

[10]陆宗骐.C/C++图像处理编程[M].北京：清华大学出版社，2005：200-320.

[11]李牧，闫继红，李戈，等.自适应Canny算子边缘检测技术[J].哈尔滨工程大学学报，2007，28（9）：1002-1007.

[12]Calvin M，Qi R，Raghavan V.A linear time algorithm for computing exact euclidean distance transforms of binary images in arbitrary dimensions[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25（2）：265-270.

[13]刘金义，刘爽.Voronoi图应用综述[J].工程图学学报，2004（2）：125-132.

[14]Srisang W，Jaroensutasinee K，Jaroensutasinee M.Segmentation of overlapping chromosome images using computational geometry[J].Walailak J Sci&Tech，2006，3（2）：181-194.

[15]Madian N，Jayanthi K B.Overlapped chromosome segmentation and separation of touching chromosome for automated chromosome classification[C]//Proceedings of IEEE Annual International Conference on Engineering in Medicine and Biology Society（EMBC），Aug 28，2012：5392-5395.