基于核密度估计的上证A 股收益率分析①

黄 雯

(铜陵学院，安徽 铜陵244000)

0 引 言

经过近二十年的发展，我国的股市越发成熟和完善.因此，学术界针对我国股票市场的相关研究也越来越多，研究的成果也比较丰富，目前跟市场有关的研究普遍与股市收益率有关.正是由于收益率的随机性透漏了投资风险的相关信息，以致于人们更加关注收益率随机性的重要性，认为其是决定是否能投资的信号.

由于经典经济学理论大多数都是建立在正态分布、对数的正态分布理论基础之上，因此线性范式在当代的金融经济学中长期处于主流地位.股票市场收益率可以反映一段时间内股市波动情况，为了方便研究分析，在经典的计量模型中股票市场收益率往往被假设为是服从正态分布的.而事实上，仍有比较多的学者对此持质疑态度，他们经过多方研究并最终认为股票市场收益率被假设为服从正态分布是错误的.因为几乎所有的股票价格的变动情况都呈现一种尖峰现象，意味着其在平均值附近的数据值比正态分布明显要多，不少学者发现正是因为某些异常值的存在导致了这种尖峰分布，因此在研究过程中通常会剔除这些异常值.比如，陶亚民(1999)在去掉了“异常值”的条件下，经过研究发现沪市收益率是呈正态分布特征的.但是Mandelbrot(1963)认为“异常值”的存在并非是偶然的，因为几乎所有股票收益率数据的共同特征就是尖峰和肥尾，所以这些“异常值”恰好说明了股票收益率不服从正态分布的假设，不能简单地将它们从数据中剔除掉.陈启欢(2002)在对我国股票市场收益率分布曲线进行实证分析时，也发现我国股市收益率并不服从正态分布.

事实上，要想准确描述经济变量之间的关系模式并不容易，因为它们并不是简单的线性模式或可以转化为线性关系的非线性模式.一旦模型假设条件与实际情况不符合时，那么估计结果就会有误差.这种情况下，根据经典假设模型做出的推断，其可信度很低.为了防止经典参数模型导致的模型设定误差，并能准确描述尖峰分布的特征，因此我们选择非参数估计方法来解决这类问题，它能针对经济变量之间的非线性关系作出较为准确的估计.所以，本文在收益率呈非正态分布的基础上，以上证A 股指数收益率为对象，采用非参数核密度估计方法对其进行研究分析.

1 核密度估计方法简介

作为估计随机变量密度函数的核密度估计，是非参数估计方法的其中一种.而我们常用的参数估计，例如传统的线性与非线性回归，都是在假设变量之间存在确定函数形式的基础上进行估计的.而在非参数估计中，自变量和因变量的分布都可以是未知的，并且对变量之间的函数形式也没有任何限定，具有很强的灵活性.因此，在变量分布和函数形式都不确定的情况下，非参数估计能为确立变量间的回归方程式提供很好的方法，并且其结果的准确性也更高.

核密度估计的思路方法如下:

假设总体分布未知，已知其密度函数为f(x)，而x1，x2，…，xn是从总体中抽取的独立同分布样本，现在我们要利用这些样本的信息，对每个x 对应的f(x)值作出估计.

直方图估计作为最典型的密度估计方法，从中能够推导出核密度估计.在使用直方图估计时，首先将直线用点分割成许多节点与长度均固定的计数区间.设独立同分布样本x1，x2，…，xn落在第i 个计数区间［ai，ai+1)里的单位数为Ni，那么在［ai，ai+1)区间范围内，密度函数f(x)的估计值就可以表达为:

显然这种情况下阶梯函数是直方图估计的结果.假如对于每一个x 的取值，都以其为中点，各做一个统计区间［x－h，x+h)，并记录下落在该统计区间的样本个数，记为N(x，h)，则对密度函数的估计可以写成如下形式:

在核密度估计中，能够将点一直维持在计数区间的中心，因为其分割区间的节点不是确定的，是随着x 的变化而改变的.这是它与直方图估计最大的区别.但是在这种情况下，通常计数区间的宽度h 是相等的.此时假如引进均匀核函数K0(x)=那么区间划分节点可变的的密度函数其估计值可表达为:

在此基础之上，Parzen(1962)发现，降低对该核函数形式的约束，只要保证其积分为1(最好还为恒正)，就可以推导出密度核估计的一般形式:

式中h 为窗宽，K(·)为核函数.

除此之外，核密度估计还可以由经验分布函数推导出来.我们可以用经验分布函数F(x)=中小于x 的个数)来表示落在以x为中心，窗宽为2h 计数区间里的样本个数，它是一种从－∞一直计到x 为止的计数方式.此时估计的密度函数为:

核函数形式放宽后，一般来说，要求核函数满足以下条件:

在选择核函数时，可以考虑概率密度函数，因为上述条件，普通的概率密度函数通常都能达到的.而对于窗宽h 的选择，要考虑到它与样本数的关系，通常窗宽与样本数是呈反比的，但窗宽也不能太小，窗宽是样本数的函数，且满足上面给定的核函数条件和窗宽条件，那么密度函数f(x)的核估f(x)计就是f(x)的渐近无偏估计和一致估计.

下面介绍几种常用的核函数:均匀核K0(x)高斯核 K1(x)=(2π)－1/2exp(－x2/2)，Epanechnikov 核K2(x)=0.75(1－x2)，三角形核K3(x)=(1－|x|)，四次方核，六次方核K7(x)通常在大样本的情况下，非参数估计对核函数的选择并不敏感，但是，窗宽h的选择对估计的效果影响较大.一般来说，h 取值相对越大，f(x)的函数曲线就相对平滑，可是其产生的误差也有可能变大.相反，假如h 取值相对较小，最后形成的密度函数图形与样本取数较为吻合，却又变得不平滑，也就是方差稍大.因此，窗宽h 的任一取值不能同时满足密度函数估计的误差缩小和方差变小.所以，在实际操作中，选择窗宽h时需要在核密度函数估计的误差与方差之间做好平衡，其积分均方误差AMISE(^f(x))成为最小值时的h 值就是其最优选择.选择h 的方法有许多，比如交错鉴定选择法，直接插入选择法，在每个局部选择各不相同的h 值，也可以估计出一个较为平滑的关于窗宽h 的窗宽函数等^h(x)2.

可以证明，在很一般的正则条件下，使积分均方误差极小化的任何h 取值一定与n－1/5成比例［3］.由此得到，一般的最佳窗宽选择为h=cn－1/5(其中c 为常数)，通过不断地调整c，使得所采用的窗宽h=cn－1/5的核估计达到满意的估计结果.h 的两个常见选择为:

其中，n 为样本个数.s 为xi的标准差为数据的0.75 分位数估计值和0.25 分位数估计值之差.因子1.059 实际上就是(4/3)1/5，是通过最优性证明得出的，因子0.785 是1.059 除以1.349 得出的，1.349 是标准正态分布的四分位数中间跨度.

2 实证分析

2.1 数据和模型说明

本文主要研究上证A 股指数收益率波动的密度估计模型.上海证券交易所上市的股票数目要远大于深圳证券交易所，又因B 股市场规模与交易量小，故选择了上证A 股指数作为研究对象.数据方面，本文采用wind 资讯公司提供的2010 年1 月至2014 年11 月12 日期间我国上证A 股日收盘指数为指标.模型方面，采用上证A 股指数日收益率Ri+1为变量.是第t 日的收盘指数，Pt+1是第t+1 日的收盘指数.另外，本文的模型估计是通过使用R 软件来实现的.

2.2 上证A 股指数收益率的密度估计

2.2.1 收益率分布的正态性检验

本文利用Shapiro－Wilk(夏皮罗－威尔克)W统计量对样本作正态性检验.在R 软件中，shapiro.test()函数提供了W 统计量和相应的p值，当p 值小于某个显著水平α(比如5%)时，则认为样本不是来自服从正态分布的总体;否则认为样

本是来自服从正态分布的总体.在此，假设上证A股指数收益率服从正态分布，得出的检验结果如下:

表1 上证A 股指数收益率的正态性检验结果

从上述结果可以看出，上证A 股指数收益率不服从正态分布.

2.2.2 选择核函数形式

在密度估计前，先要通过模拟选择合适的核函数.本文选用两种常见的核函数:高斯核，四次方核来进行比较，看哪种核函数的拟合效果最好.运用R 软件进行模拟，得出如下结果:

图1 两种核函数估计与正态密度曲线

注:上图中，峰度最低的表示正态密度曲线，峰度最高的表示四次方核估计，峰度介于中间的表示高斯核估计.

图1 显示两种不同核函数估计的效果，可以发现在这种情况下，与四次方核估计相比，高斯核估计要更光滑，也更接近真实的密度函数，所以本文选用高斯核函数对数据进行拟合.

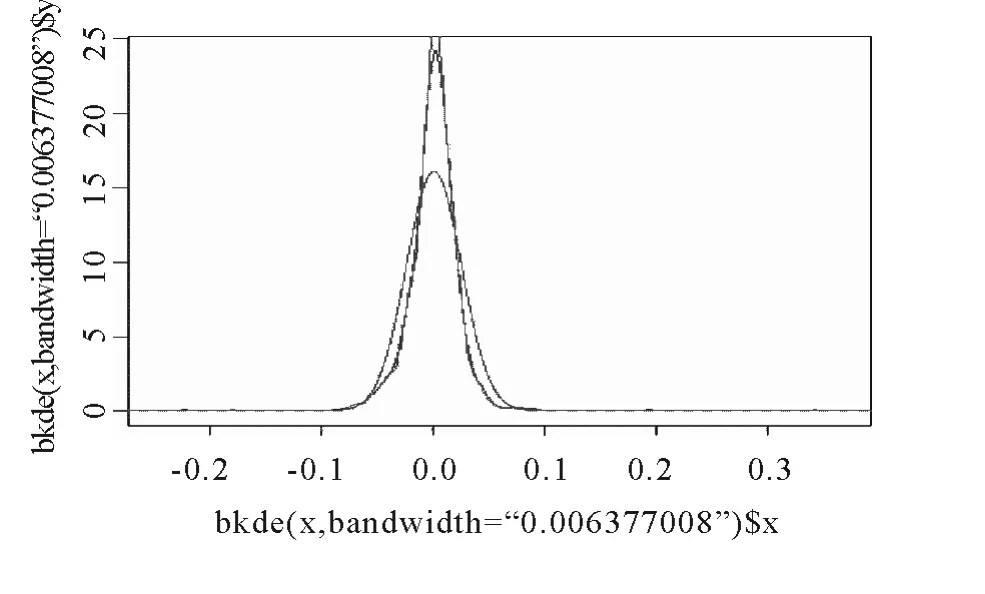
图2 两种常用窗宽下的高斯核估计和正态密度曲线

2.2.3 窗宽的选择

同样，在密度估计前，也要通过模拟选择合适的窗宽.本文在选用高斯核函数对数据进行拟合的条件下，选取上述(3)式和(4)式介绍的两个常见的窗宽来进行比较.由(3)式和(4)式分别计算得出h1=0.006376，hM2=0.003952.运用R 软件进行模拟，得出如下结果:

注:图中，峰度最低的表示正态密度曲线，峰度介于中间的表示h1窗宽下的高斯核估计，峰度最高的表示h2窗宽下的高斯核估计.

图2 显示出，窗宽下的高斯核估计更光滑，更接近真实函数，所以本文选用h1=0.006376 作为高斯核估计的窗宽.

3 非参数估计下的上证A 股指数收益率密度函数的实际应用

在核估计的核函数与窗宽都确定后，就可以得到上证A 股指数收益率的核估计密度函数的确定形式:

在非参数核密度估计的情况下，收益率的期望和方差为:

通过公式(6)，(7)，(8)，可以计算出核估计密度函数的期望与方差，见表2:

表2 上证A 股指数实际收益率与非参数估计下收益率的统计特征对比

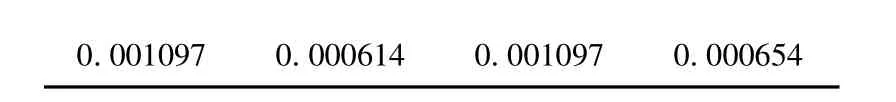
0.001097 0.000614 0.001097 0.000654

从表2 可以看出，实际数据的均值与核估计收益率的期望是相同的，但是方差却不一样，核估计的方差比实际数据的方差偏大.这说明厚尾是上证A 股指数收益率分布呈现出的特征.

由于本文采用的是高斯核(正态核)函数，所以可以推导出核估计条件下的收益率分布函数是:

从上面公式中，能够得知基于核密度估计的收益率分布的函数形式，这样我们就可以把收益率落在不同区间内的概率计算出来，具体结果见表3:

表3 上证A 股指数收益率的区间概率值

表3 的计算结果表明:上证A 股指数的收益率下跌超过5%的概率值为2.195%，而上涨超过5%的概率值为1.491%，下跌的的可能性大于上涨的可能性.这说明近年来我国上证A 股市场不景气，我们认为可能是受到金融危机的影响.

4 结 语

从上个世纪末以来，非参数估计法较好的解决了未知分布模型以及不完全数据模型的处理，从而打破了传统统计学研究的瓶颈，成为统计学新的发展主题和方向.与传统的参数估计不一样，非参数估计抽取的样本不用过多关注总体的分布模式，此外，不设参数，没有限定的函数模型，而仅靠每个数据决定函数值，具有较强的灵活性.因此，在变量分布和函数形式都不确定的情况下，非参数估计能为确立变量间的回归方程式提供很好的方法，并且其结果的准确性也更高.

本文采取实证研究的方法，利用非参数估计——核密度估计法，针对上证A 股指数收益率分布状态作出深入研究.研究发现，非参数核密度估计方法能够较好地描述股票收益率分布的尖峰厚尾的特征，能够较为准确的反映收益率分布具体情况.除此之外，在本文的研究过程中还得出上证A 股指数收益率在核密度估计情况下的期望与方差，以及其在不同区间取值的概率情况.通过比较分析各个区间的概率值，揭示了近年来上证A 股市场的特征.

［1］ 陶亚明，蔡明超，杨朝军.上海股票市场收益率分布特征的研究［J］.预测，1999，(2):57－58.

［2］ 李子奈，叶阿忠.高等计量经济学［M］.北京:清华大学出版社，2000.

［3］ 陈启欢.中国股票市场收益率分布曲线的实证［J］.数理统计与管理，2002，(5):9－11.

［4］ 孔凡秋.套期保值的下偏矩风险评价［D］.武汉:武汉理工大学，2004.

［5］ 陈娟.非参数方法在沪深股市收益率分布的应用［J］.温州大学学报，2005(3):22－27.

［6］ 吴喜之.非参数统计［M］.北京:中国统计出版社，2006.

［7］ 薛毅，陈立萍.R 软件建模与R 软件［M］.北京:清华大学出版社，2007.

［8］ 施祖麟，黄治华.基于核密度估计法的中国省区经济增长动态分析［J］.经济经纬，2009，(4):60－63.

［9］ 张世趟，程小军，苏明.基于非参数方法的A 股指数估计［J］.南方金融，2009，(1):25－27.

［10］ 镇志勇，李军.非参数核密度估计在恒生指数收益率分布中的应用［J］.统计与决策，2011，(9):22－24.