对储药柜优化设计模型的进一步研究①

张宇玉

(山西机电职业技术学院，山西 长治046011)

0 引 言

智能化的储药柜越来越多的运用到各大医院，药房药品种类繁多，为能使药品准确取出并合理利用空间，储药柜药槽的合理设计尤为重要.本文基于2014 年全国大学生数学建模D 题数据，给出储药柜优化设计方案.

1 问题一的模型建立及求解

问题一是根据所给药盒的尺寸数据，同时考虑到题目要求“两侧竖向隔板之间应留有2mm 的间隙”和“推送过程中不会出现并排重叠、侧翻、水平旋转”的条件，给出竖向隔板间距类型最少的储药柜设计方案.

其中的条件可转化为数学不等式.不出现并排重叠其实就是要求药槽的宽度不大于药盒宽度的2 倍，即

不出现侧翻就是要求药槽的宽度不大于药盒的宽高对角线，即

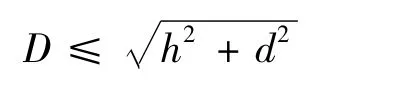
不出现水平旋转就是要求药槽的宽度不大于药盒的长宽对角线，即

所以问题一转化为规划模型［1］解决.

目标函数为 mini (i 为竖向隔板的类型)

约束条件为:

问题一就是在上述条件下求出竖向隔板最少的类型.先用Excel 软件［2］计算出药盒的宽高对角线值和2 倍宽度值，再将宽度按升序排列，筛选出最小宽度和宽高对角线，根据约束条件给出药槽规格范围，然后由题目要求“药槽宽度种类最少”，得到药槽宽度，从而容易知道适用的药盒宽度范围.第二步将第一次排序适用的药盒删除，剩余的药盒进行升序排列，同理按照第一次排序的步骤进行，得到第二类药槽宽度，依次进行下去，最终得到4类药槽宽度和药盒宽度范围.具体方案如下表1 所示.

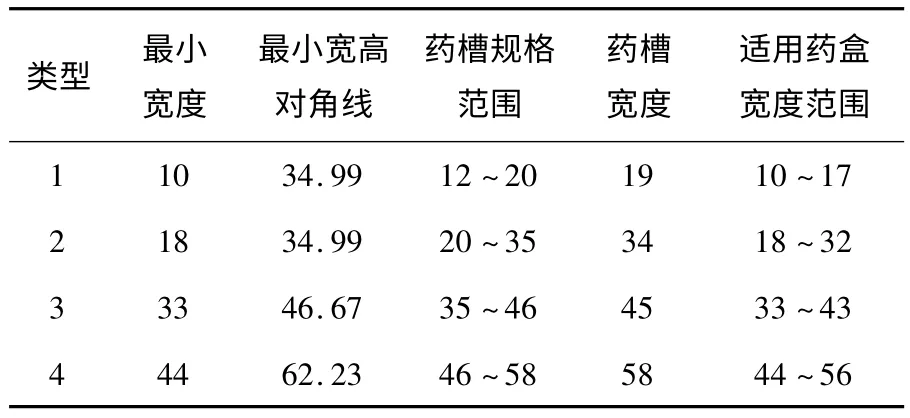
表1 最少药槽宽度类型及对应的药盒宽度范围(单位为mm)

2 问题二的模型建立及求解

定义，每种宽度冗余=(药槽宽度－药盒宽度－2)×药盒数量，则总宽度冗余就是所有类型宽度冗余的和.

药盒按宽度升序排列后，统计出每种宽度下的药盒数量.药盒宽度最小为10mm，最大为56mm，若划分为47 种类型，即每一种药盒宽度为一类，则总宽度冗余为0.按照药盒数量均匀划分原则［3］，例如将药盒宽度分为5 种类型，已知有1919 个药盒，则每种类型下的药盒数量为个，由此可确定出每种类型下的药盒宽度范围和药槽宽度.将药盒宽度分为4 ～11 种类型，给出了每种类型下的药槽宽度，并计算出每种类型下的总宽度冗余量［2］.根据表中药槽宽度类型数和冗余量之间的关系用平滑散点图表示，具体见表2，图1.

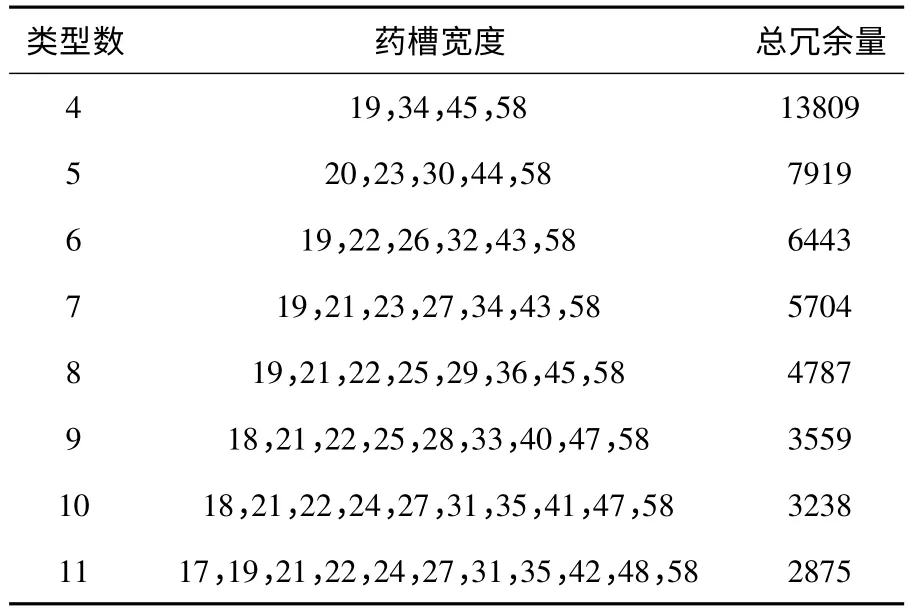
表2 药槽宽度类型与总冗余量

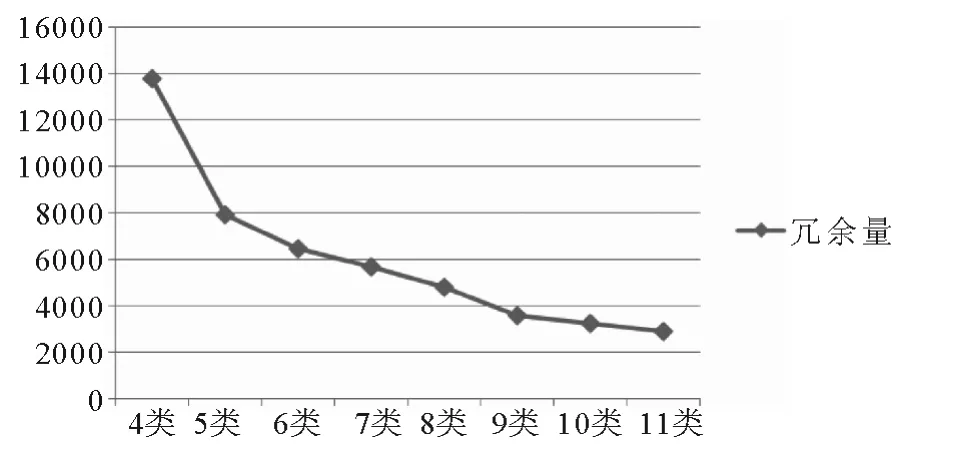
图1 宽度冗余量与药槽宽度类型数的关系图

从图1 中可看出开始随着类型数的增加，总宽度冗余量下降得很快，9 种类型之后的宽度冗余量也在减少，但是幅度较小.增加类型会降低宽度冗余量，但是也会增加药柜的生产成本，所以我们选择10 种作为合理的药槽宽度类型数.具体的药槽宽度类型及适用的药盒宽度范围见表3.

表3 宽度冗余尽可能小的药槽宽度类型与适用的药盒宽度范围

3 问题三的模型建立及求解

问题三处理方式与问题二相同，问题二已经求出在尽可能小宽度冗余下的药槽宽度类型.问题三要求在最小的平面冗余下的药槽高度类型.

由于，问题二的结果已经是最小的宽度冗余，现在只需找到最小的高度冗余下的药槽高度类型即可.

定义 高度冗余=(药槽高度－药盒高度－2mm)×药盒数量

将药盒按高度升序排并统计出每种高度下药盒的数量.同问题二，我们按照药品数量均匀划分原则［3］，将药槽高度类型分为4 ～19 种类型，分别计算出每种类型下的总高度冗余量［2］，然后将药槽高度类型数和高度冗余量之间的关系用平滑散点图表示，如图2 所示

图2 药槽高度类型数和高度冗余量之间的关系

图2 中可看出开始时总高度冗余量下降得很快11 种类型之后的宽度冗余量也在减少，但是幅度较小.增加类型会降低高度冗余量，但是也会增加药柜的生产成本，所以我们选择12 种作为合理的药槽宽度类型数.具体的每种类型下的药槽宽度及适用的药盒宽度范围见表4.

表4 平面冗余尽可能小的药槽高度类型及药盒范围

问题二得到宽度冗余尽可能小的情况下的药槽宽度类型为10 种，问题三得到平面冗余尽可能小时的药槽高度类型为12 种.将每一种药槽类型下的药盒数量进行统计，结果如表5 所示.

表5 每种药槽类型下的药盒数量

将每个高度槽内的药盒宽度+2mm 再求和，然后除以2500 取整，就得到每种高度的最小层数，见表6.各类药槽高度与其层数乘积之和为1425mm ＜1500mm，符合储药柜的设计要求.

表6 每种药槽高度所需的层数

4 问题四的模型建立及求解

用储药槽的长度分别除以每种药盒的长度，可得到每个储药槽中药盒的个数，再用每种药品的最大日需求量除以每个储药槽中的药盒个数，便可以得到每种药品需要的储药槽个数.公式为

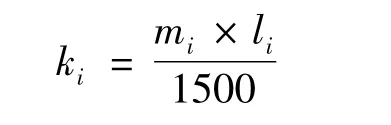
其中ki表示第i 种药品需要的储药槽个数，mi表示第种药品的最大日需求量，li表示第i 种药品的长度，i 为药盒种类.

通过求解，并取整得到每种药品需要的储药槽个数，如表7 所示

表7 每种药品所需的储药槽个数

由于一个储药柜要满足1919 种类型的药盒，并且一个储药槽只能放一种药，因此只需一个储药槽的药盒用一个储药柜即可满足需要，所以我们将所需药槽个数大于1 的药品类型以宽度进行升序，得出同种宽度区间内对应药品所需储药槽个数总和，结合问题三的规格(表5)可知，在同一类型药槽兼容性下，满足需求量需2 个储药柜.

5 结 语

本文能够根据题目要求，将问题一转化为规划模型，然后利用Excel 软件中的筛选、公式计算、分类汇总等功能处理数据，提高了解决问题的效率.另外，将药品等数量划分，并计算出相应的冗余量，可以找到冗余量较少和最少药槽宽高度类型的平衡点，但不是很准确，需要进一步研究此问题.

［1］ 姜启源.数学模型［M］.北京:北京高等教育出版社，2009.

［2］ 吴权威.Excel 2003 应用基础教程［M］.北京:中国铁道出版社.2004.

［3］ 薛毅，刘保东.储药柜设计问题解析［J］.数学建模及其应用.2014，4(3):59－65.

［4］ 谢金星，薛毅.优化建模与LINDO/LINGO 软件［M］.北京:清华大学出版社，2011.