基于变分方法的一类二阶微分方程周期解的研究①

邓瑞娟，施吕蓉

(芜湖职业技术学院，安徽 芜湖241000)

根据积分中值定理知必存在ζ ∈［0，T］，使得

下面证明存在ζ* ∈［0，T］，使得

0 引 言

具偏差变元的微分方程自创立起，就受到广泛关注，主要是因为其有着丰富的应用背景.而自然界中很多现象都有一定的周期性，所以对微分方程周期解的研究也从未停歇.多年来，也得到了一些的结论［1～8］.

如文献［7］，讨论了如下形式的二阶微分方程:

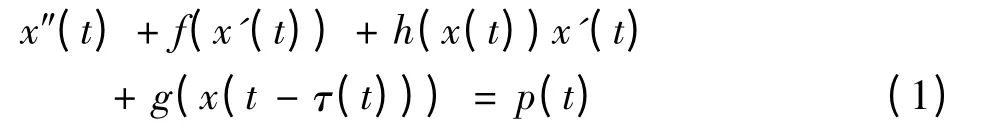
并给出了T-周期解存在的两个充分条件.而文献［8］则针对其中的一个定理进行了推广.本文利用Mawhin 延拓定理，得到了方程(1)关于周期解的一个新结论，进一步完善了文献［7］和文献［8］的工作.

方程(1)中f(x)，g(x)，h(x)，p(t)均为R 上的连续函数，其中p(t)，τ(t)都是以T 为周期的函数.在文献［7］和［8］中均假设，本文无需这一假设，这也使得本文的结论应用更为广泛.

2 相关记号和引理

于是

因此L 是指标为零的Fredholm 算子.设定义投影算子P，Q 分别为

则ImP=KerL，KerQ=ImL.令Lp=L|D(L)∩KerP，则Lp是可逆的，其逆为

下面给出本文将会使用到的引理、定理.

引理1［4］设有Banach 空间X，Y，Ω ⊂X 为有界开集，L 是指标为零的Fredholm 算子，N 在上是L-紧的，若同时满足下列条件满足:

(1)对∀λ ∈(0，1)，x ∈∂Ω ∩D(L)，有LxλNx;

定理A［8］若存在K ＞0，K1＞0，D ＞0，m ＞0 使得

(1)|f(x)|≤K，∀x ∈R，，且f(0)=0;

(2)x(g(x)-p(t))＞0，且|g(x)|＞K，当|x|＞D 时;

(3)|h(x)|≤K1，∀x ∈R;

(4)g(x)-p(t)≥-m，当x ≤-D.

且1-TK1＞0，则方程(1)至少存在一个T-周期解.此定理中要求

3 主要结果及证明

定理1 如果存在常数σ1≥0，σ2≥0，K ＞0，K1＞0，M ＞0，使得方程(1)满足条件

i |f(x)|≤k+σ1|x|，∀x ∈R;

ii x(g(x)-p(t))＞0，且|g(x)-p(t)|＞k+σ1x，当|x|＞M 时;

iii |h(x)|≤K1，∀x ∈R;

则当T(2σ1+2σ2+2ε+K1)＜1 时，方程(1)存在T-周期解.

证明: 对∀λ ∈(0，1)，作辅助方程

记Ω1={x|x ∈D(L)，Lx=λNx，λ ∈(0，1)}，显然Ω1为辅助方程(2)的所有T-周期解组成的集合，∀x ∈Ω1，对方程(2)两边从0 到T 积分，由于x(t)，x′(t)的周期性，有

根据积分中值定理知必存在ζ ∈［0，T］，使得

下面证明存在ζ*∈［0，T］，使得

情形1 若σ1=0，则定理1 中条件i 变成:i′|f(x)|≤k，∀x ∈R.

现假设|x(ζ-τ(ζ))|＞M，由i′和ii 可得k ＜|g(x(ζ-τ(ζ)))-p(ζ)|=|f(x′(ζ))|≤k

显然这是矛盾的，于是有

情形2 若σ1＞0，同样假设|x(ζ-τ(ζ))|≥M，则由定理条件i 和ii，可得

由(6)式可知

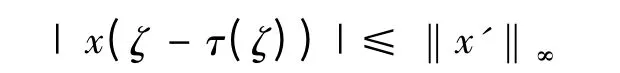
由上述讨论可知，对于σ1≥0 时，必有

考虑到ζ-τ(ζ)∈R，故一定存在m ∈Z，ζ*∈［0，T］，使得ζ-τ(ζ)=mT+ζ*，于是|x(ζτ(ζ))|=|x(ζ*)|≤‖x′‖∞+M，故(5)式成立.又因为

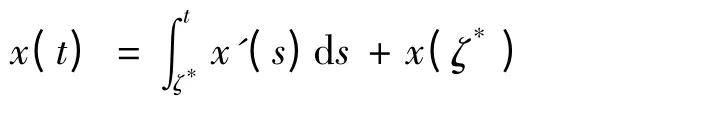
所以

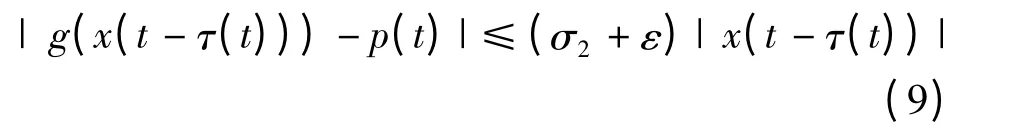
根据x 与D 的大小关系，做如下假设:E1={t|t ∈［0，T］}，x(t-τ(t))＞D}，E2={t|t ∈［0，T］，x(t-τ(t))＜-D}，E3={t|t ∈［0，T］，|x(t-τ(t))|≤D}.由(3)式可知，

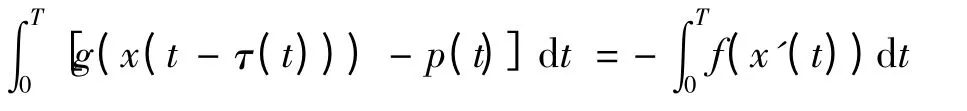
下面估计，

因此可得，

因此，

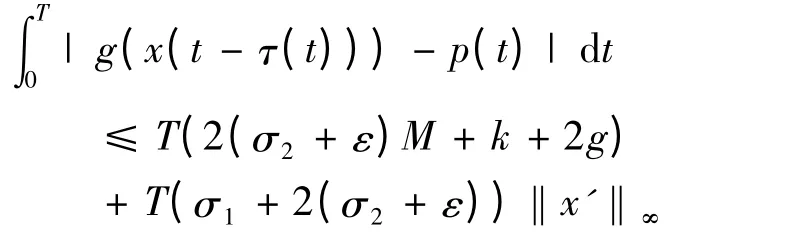
其中.由(2)式可得

因为x(0)=x(T)，由罗尔定理可知必存在η*∈(0，T)，使得x′(η*)=0，所以得

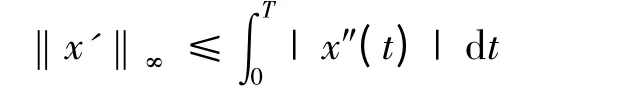
由(9)式可得

其中，r1= T［2(σ1+σ2+ε)+K1］＜1，r2=2T((σ2+ε)M+k+g)，将上式整理可得

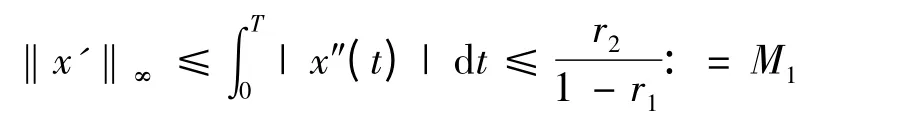
同时有:

显然M1，M2为与λ，x 无关的常数，故Ω1为有界集.后续证明同文献［7］中定理2 的证明，此处略.证毕.

文中研究的方程与文献［7］，［8］研究的方程相同，但是后两者均要求，而本文无此假设.因此，本文的结论是关于方程(1)周期解问题的新结果.

作为应用，考虑如下方程:

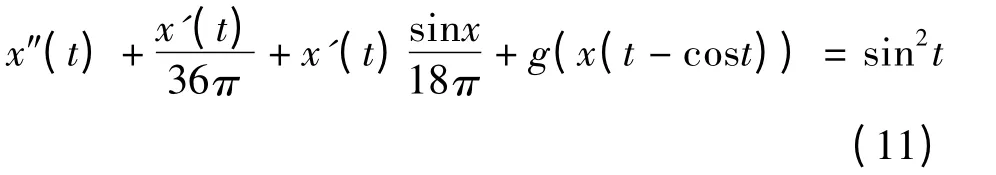
其中

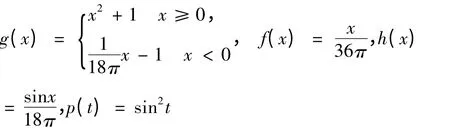
［1］ 葛渭高.一类n 维–Liénard 方程的调和解［J］.数学年刊，1990，11A(3):297－307.

［2］ 施吕蓉，周宗福，高伟.一类二阶具多偏差变元微分方程的周期解［J］.山西师范大学学报(自然科学版)，2012，26(4):12－17.

［3］ 王鲁新，李聚臣.一类三阶具多偏差变元微分方程的周期解［J］.佳木斯大学学报(自然科学版)，2009，27(5):793－796.

［4］ 郭承军，王根强.一类二阶具多偏差变元微分方程周期解的存在性［J］.中山大学学报(自然科学版)，2007，46(6):5－9.

［5］ 汪娜，鲁世平.一类三阶具偏差变元微分方程的周期解［J］.安徽师范大学学报(自然科学版)，2006，29(1):17－22.

［6］ Omari P.，，Zanolin P.，Anote on Nonlinear Oscillation at Resonance，Acta.Math..Sinica.，1987，3(3):351－361.

［7］ 杜波，鲁世平.一类具偏差变元的二阶微分方程周期解［J］.数学研究，2007，40(1):16－21.

［8］ 刘道金，鲁世平.一类具偏差变元的二阶微分方程周期解［J］.杭州师范大学学报(自然科学版)，2009，8(5):354－357.