基于E－MS 算法的含缺失数据图模型选择的模拟研究①

孙聚波，徐平峰

(长春工业大学 基础科学学院，吉林 长春130012)

0 引 言

在统计分析中，列联表是分类数据的一种常用、直观的表示方法［1］.很多高维分类数据都具有某种特殊结构，通常可以用图模型表示［2］.其中，模型选择是统计推断的重要方面，许多学者提出了各种各样的方法，例如，Akaike 提出了基于似然的AIC 准则［3］，Schwarz 提出了BIC 准则［4］，Edwards和Havranek［5］提出了从大规模模型族中选择出可接受的一组模型等等.当数据有些值缺失时，模型选择的最新成果是，Jiang，Nauyen 和Rao 于2014年提出的E－MS 算法［6］.本文对于含有缺失值的列联表数据，在E－MS 算法的框架下，进行图模型的模型选择，其中广义信息准则采用BIC 准则.对于含3、4 和5 个分类变量的情形进行了模拟实验.

1 列联表及图模型

1.1 列联表的概率结构

一般来说，观测数据按两个或多个属性分类时所列出的频数表称为列联表.本文中，令V 表示分类变量的集合.对分类变量γ ∈V，Yγ表示γ 的有限的水平集，YV=×γ∈VYγ表示分类集V 的水平集，则列联表中的一个格子对应集合YV中的一个元素y=(yγ)γ∈V.把n 个观测个体按V 进行分类，令计数xy为落入格子y 的观测频数，则这些计数xy的集合便构成了一个列联表，记作X={xy|y ∈YV}，且设一个个体落入格子y 的概率为p(y)，满足p(y)3≥0，且于是整个表的联合概率分布是一个多项分布:

在高维列联表中，饱和模型的参数个数一般大于样本量，不仅统计上无法处理，计算上也不可行.但事实上，很多高维数据都具有某种特殊结构，可用图模型表示，以减少参数个数.

1.2 图模型及其概率分解

在图模型中，随机变量由图的顶点表示，有直接关联随机变量，对应的顶点用边相连，这样构成一个图G(V，E)，这里V 为顶点集，E 为边集.相对于图G 满足马尔科夫性的概率分布族，即为图模型［3］.在图模型中，可利用图的语言表示概率统计相关问题，并依据图论的理论和算法帮助进行概率统计推断［2］.

在图G 中，如果子集c ⊆V 中任意两个顶点都是相连的，则称c 是完全的.如果完全子集c 相对于包含运算而言是最大的，称它为团，K(G)为图G的所有团的集合.对于团c，称yc=(yγ)γ∈C为边缘格子，相应的边缘计数为，边缘概率为许多学者指出，马尔科夫性与概率的基于团的对数展开形式之间存在等价关系.其中，Lauritzen［2］给出了严格的数学叙述:概率p 相对于图G 满足马尔科夫性当且仅当存在函数φc(yc)满足将该式变形得p(y)=于是p 的参数为θG={φc(yc)，c ∈K(G)}.分解后参数个数大大减少.例如，每个变量取2 个值，则p(y)分解后需要个参数来描述，远远小于饱和模型下的参数个数2|v|.

1.3 图模型的极大似然估计

图模型的统计推断中，求参数的极大似然估计是非常重要的一个方面.对于列联表X，对数似然为:

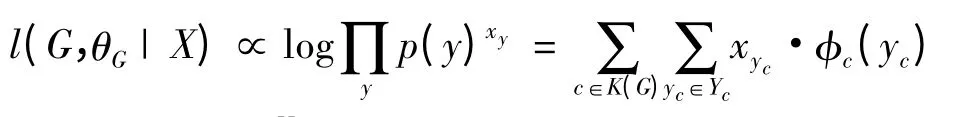
Lauritzen［3］证明了上式中极大似然估计^p 的唯一性，给出了相应的似然方程组:

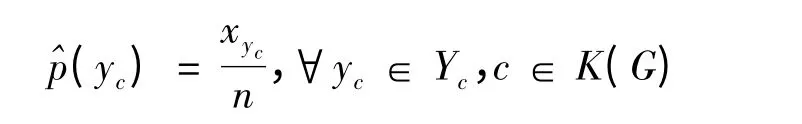
上述似然方程组往往可采用迭代比例拟合(IPS)算法［3，4］来求解.在投往CSDA 的论文中给出了基于团分划改进的IPS 算法［7］.

当数据含缺失值时，记观测数据为Xobs，此时可用EM 算法求极大似然估计.设qtG 为当前参数值，则E 步为求，M步对Q 函数关于团求导得，对所有的yc∈Yc，c ∈K(G)，

2 基于E－MS 算法的缺失数据的图

运用E－MS 算法进行缺失数据的图模型选择.首先规定图模型选择空间为所有可能的图模型的集合G.在E－MS 算法的E 步中，当前图模型Gc以及Gc的当前参数估计，令θG为候选图模型G 的参数.定义Q(G，θG)为给定观测数据Xobs下，完全数据X 的对数似然的条件期望，即:

图模型G 的改变对BICG值的影响远大于θG的变化对BICG值的影响，所以在模拟中，若连续5 次迭代的最优图模型^Gopt都为同一个模型，就停止迭代.

3 模拟研究

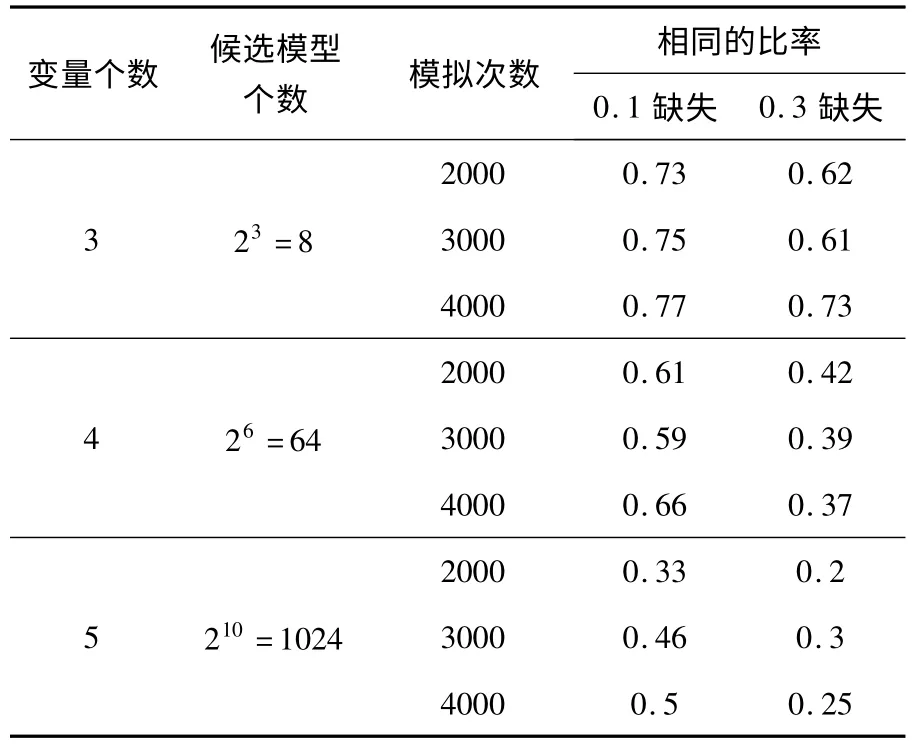
表1 E－MS 算法选择的模型与真模型相同的比率

在表1 中，随着变量个数增加，经E－MS 算法选择的模型与真模型相同的比率有所下降，这是因为候选模型个数成指数型增长.实际工作中，可根据其他先验知识或方法缩小候选模型的空间，提高准确率.另外，表2 给出了多边比率和少边比率.其中多边比率为选择的多余的边数除以真模型的边数，再求平均值;少边比率为没有找的真模型中的边数除以真模型的边数，再求平均值.由表2 可分析出，数据缺失概率越大，经E－MS 算法选择的模型与真模型不同的边数越大;其次随着样本量的增加，相同缺失概率下，E－MS 算法选择的模型与真模型边数不同的比率在减小.总的来说，无论在哪种情形，多边比率与少边比率之和不大于0.4，也就是说我们可以至少0.6 的概率正确的判断边是否存在.

表2 E－MS 算法选择的模型与真模型的比较

4 结 语

通过对模拟研究的分析可知，E－MS 算法在候选模型个数较少时具有良好的性能，当候选模型个数非常多时，E－MS 算法的性能下降较多，这也是现在大多模型选择方法的共同不足之处.对此，可结合其它方法或先验知识缩小候选模型集合，然后再利用E－MS 算法进行模型选择.

［1］ Agresti，A 著，张淑梅，王睿，曾莉译.属性数据分析引论［M］，第二版.北京:高等教育出版社，2008.

［2］ Lauritzen，S L.Graphical Models［M］.Oxford:Clarendon Press，1996.

［3］ Akaike，H.An Information Criterion［J］.Math Sci，1976.

［4］ Schwarz，G.Estimating the Dimension of a Model［J］.Annals of Statistics，1978，6(2):461－464.

［5］ Edwards，D，Havranek，T.A Fast Model Selection Procedure for Large Families of Models［J］.Journal of the American Statistical Association，1987，82(397):205－213.

［6］ Jiang，J，Nauyen，T，Rao，J S.The E－MS Algorithm:Model Selection with Incomplete Data［J］.To appear in Journal of the American Statistical Association，2014.

［7］ Xu，P F，Sun，J，Shan，N.Local Computations of the Iterative Proportional Scaling procedure for Hierarchical Models［J］.Revised in Computational Statistics and Data Analysis，2015.