升力体高超声速飞行器非定常滚转力矩建模研究
高 清,李建华,李 潜
(中国航天空气动力技术研究院,北京 100074)
升力体高超声速飞行器非定常滚转力矩建模研究
高 清,李建华*,李 潜
(中国航天空气动力技术研究院,北京 100074)
为了深入研究升力体高超声速飞行器相对薄弱的横侧向稳定性问题,对滚转自由振荡风洞试验数据进行了谱分析,建立了多个气动频率余弦和形式的非定常滚转力矩模型。由于升力体高超声速飞行器的滚转自由振荡曲线呈现非定常、非线性和一定的周期性特征,且对试验结果的谱分析发现,在多种气动状态下,都存在除机械振动频率外的三个振动频率,将滚转力矩表达为此三个频率余弦和的形式。该滚转非定常气动力矩数学模型捕捉了试验的基本趋势涵盖了其主要的量值范围,反映了升力体高超声速飞行器横向流场扰流的多尺度和周期性特征。
升力体;高超声速;滚转力矩;非定常气动力;建模
0 引 言
飞行器空气动力学问题的复杂性之一就在于绕流结构的多尺度特征。飞行器绕流易出现分离和分离涡的周期性脱落。绕飞行器的来流即使是定常,也会因分离涡的周期性脱落使流动呈现非定常和非对称特征。在高超声速条件下飞行器绕流的周期性、非定常过程更加强烈,剪切流和涡结构由于轴向动量的增大被拉长,此时横向扰动极易使流动的轴向动能转化为横侧向动能。
通常在亚跨和低超声速,绕流中低频的大尺度结构能量远大于高频的小尺度结构能量,使流体动力学参数通常表现为单频、线性。但对高超声速,随马赫数的增加,绕流中高频、小尺度结构的能量及其对飞行器的影响越来越大,流体动力学参数无法继续由线性系数描述。小尺度流动结构的重要特征是流动的三维性,高超声速的横流扰动强烈,尤其是滚转力矩呈现强烈的非定常和非线性特征,必须寻求一种新的参数形式,进行非定常气动力建模。
根据泛函分析理论,广义非定常气动力可写为Duhamel积分形式[1]:
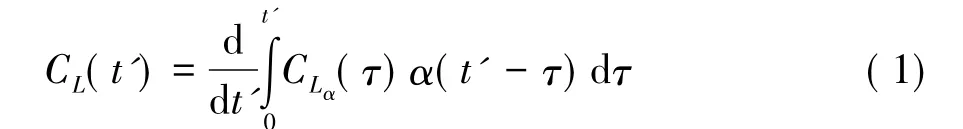
它表示飞行器绕流引起的气动力和力矩不仅与流动变量的瞬时值有关,且与其变化历程相关,但要确定机动飞行器上瞬时气动载荷和运动变量间的关系非常困难。为此,人们提出了各种假定和近似,以期找到既符合基本原理又适用于具体实践的数学表达式。
非定常空气动力建模自20世纪初在国外开始发展以来,陆续出现了多种非定常空气动力的建模方法,归纳起来大致有:积分模型[2-5]、微分模型[6-9]、状态空间模型[10-11]、神经网络模糊逻辑模型[10-19]和代数模型[20-22]。积分模型在理论上是完备的,但过于复杂,且模型中所含未知函数很难通过数值计算、风洞试验和飞行试验确定,因此很难应用;微分方程模型存在非线性项物理意义不直观、非线性项近似表达式中的人为加权函数不易确定等缺点;代数模型基于准定常假设,是最简单、最方便的非线性模型。常用的代数模型有级数函数模型和样条函数模型等。采用代数模型时,须根据物理问题选择适当的状态参数、阶次及组合项,用最少的项来逼近物理本质。
研究通过对升力体高超声速飞行器非定常气动力风洞试验数据的分析,试图建立客观直接、有明确物理意义、并具有一定工程实用指导意义的滚转力矩数学模型。
1 建模原理
研究基于风洞试验获取的非定常气动力数据,根据数据的频谱特性,分析建立一种级数形式的非定常气动力表达式。级数的项数、各项的系数、频率由风洞试验结果确定。
由于本研究中升力体高超声速飞行器的滚转自由振动曲线与Hopf分叉后的振荡曲线类似(图1),所以借鉴了Hopf分叉[23-25]后气动力的表达式,将滚转力矩表达为振动频率余弦和的形式。

图1 Hopf分叉Fig.1 Hopf bifurcation
2 建模方法
对滚转非定常气动力试验数据的谱分析发现,滚转方向的气动力矩存在多个频谱,流场特征可近似由几个主要振动频率共同描述。将滚转力矩表达为mx的形式,其中mx表示滚转力矩,an表示振幅,ωn表示根据试验结果的频谱分析得到的主要振动频率,λn表示相位。
建模过程:首先,对升力体高超声速飞行器模型的地面无风自由滚转振动数据进行谱分析(图2),获得机械阻尼的频率(10.74 Hz)。然后对四种状态下的滚转非定常气动力试验结果进行谱分析(图3),确定主要的振动频率及其幅值和相位,发现在这些状态下,试验曲线都存在除机械阻尼频率外的三个振动频率,按振动频率对应的幅值从大到小的顺序依次为:10.25 Hz、9.77 Hz、11.23 Hz。而且根据频谱图,机械阻尼对应频率10.74 Hz的幅值小于三个气动阻尼频率对应的幅值,说明在研究的气动状态下,气动阻尼在总阻尼中所占的比例较高,机械阻尼干扰相对较小。
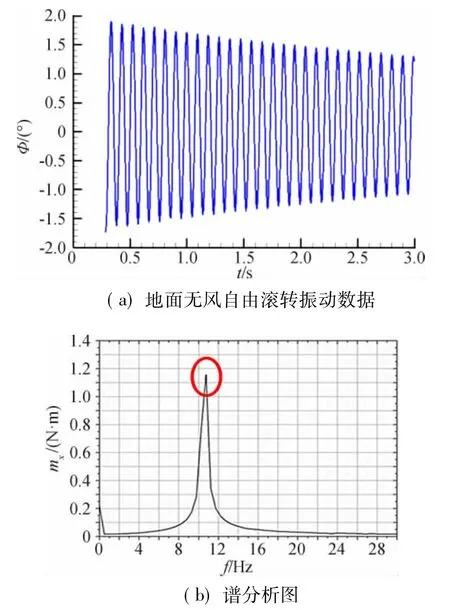
图2 地面无风自由滚转振动数据及其谱分析图Fig.2 Ground-tested roll-free-oscillation result and its spectrum analysis

图3 滚转非定常气动力试验数据及其谱分析图Fig.3 Wind-tunnel-tested roll-free-oscillation result and its spectrum analysis
滚转力矩可近似由三个振动频率的余弦函数表达为:

其中ai表示气动主频对应的幅值,λi表示相位。对于不同的气动状态,三个气动主频对应的幅值和相位稍有不同(图4)。
由图4可见,在试验研究的四种状态下,滚转力矩模型中频率项幅值存在较明显的规律性,频率项幅值随马赫数的增加而减小,随攻角的增加而略有增加,相位角随马赫数和攻角的变化也呈现一定的规律性。
本节通过对非定常气动力试验数据的谱分析,获得了模型系统的三个振动频率、幅值和相位,建立了这三个气动振动频率余弦和形式的滚转力矩数学模型。
3 建模模型的物理意义
根据动态试验相似条件,试验模型振动频率的无量纲值与真实飞行器在大气中的无量纲运动频率应相同[26]。因为只有两者相同时,真实飞行器和试验模型的绕流才是相似的。以Ma=5,飞行高度30 km配平攻角α=1.2°状态为例,真实飞行器在大气中的滚转振动的无量纲频率可表示为:
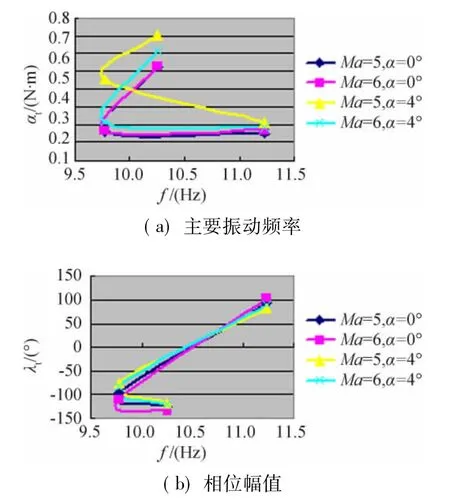
图4 主要振动频率及相位幅值Fig.4 Main vibration frequencies and their phases and amplitudes
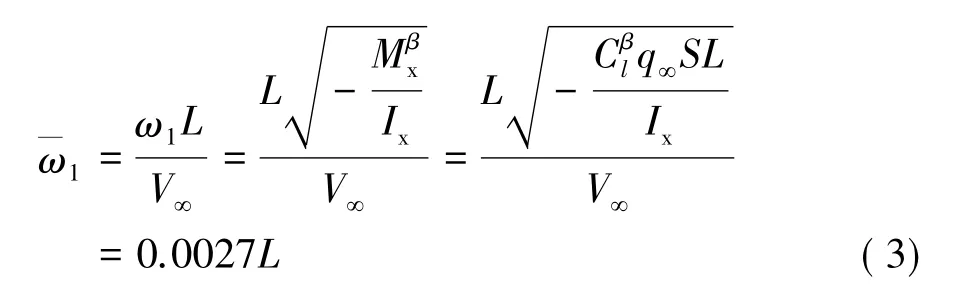
其中L表示试验模型的参考长度。
试验模型的无量纲振动频率可表示为:

根据动态试验相似关系,有:

即,横向参考长度和试验模型的振动频率之间存在式(6)的线性比例关系。对非定常气动力风洞试验数据的谱分析结果表明,模型的振动曲线存在除机械振动频率外的三个较为明显的振动频率,对应飞行器横向绕流有三个特征尺度,即横向分离或转捩流动有三个不同的尺度。这三个特征长度可根据式(6)由试验振动频率直接获得(表1)。

表1 试验振动频率与特征长度Table 1 Main vibration frequencies and their characteristic lengths
如选取飞行器的横向跨度为特征长度,则该特征长度在飞行器上的分布见图5,流场特性在这三个位置上可能出现非对称分离、转捩等变化。

图5 横向参考长度在飞行器上的位置Fig.5 Distribution of lateral reference lengths on aircraft
从流场角度分析,在高超声速飞行时,飞行器绕流中湍流与转捩等小尺度流动的贡献明显增加,不同尺度流动的频率随马赫数增加也越来越近,高超声速绕流的多尺度效应是高超声速流动有别于低速流动最重要的特征,也是高超声速飞行器气动力出现强烈非线性的根本原因之一。滚转力矩多频、非线性特征使高超声速飞行与控制面临较大困难。
4 模型的有效性
为了验证建立的三个振动频率余弦和形式滚转力矩模型模拟试验数据的效果,将各状态非定常滚转力矩数学模型数据与相应试验数据进行对比,如果趋势和量值基本一致,说明这三个气动振动主频基本可代表该气动状态主要特征,反之,则可能是气动振动主频选择不合适,或三个气动振动主频不足以描述该状态的气动特征。

图6 三个气动主频模拟数据与相应试验数据的对比Fig.6 Comparison of the model of roll moment constructed in this paper with the corresponding aerodynamic test data
图6给出Ma=5、α=0°状态下,建立的滚转力矩模型数据与试验数据的对比。可见,滚转力矩数学模型基本捕捉了试验曲线的基本趋势,也涵盖了主要的量值范围,而且周期性的表达式反映了横向力矩周期性的物理特征,可初步认定,采用三个振动主频余弦和模拟滚转力矩是适当的。
5 结 论
升力体高超声速飞行器滚转自由振荡试验发现,模型的振动具有非线性、非定常、多频、周期性特征,飞行器的滚转力矩已不能由线性系数继续描述。对该试验模型多种气动状态试验数据的谱分析表明,存在除机械振动频率外的三个振动频率。此三个振动频率对应飞行器横向绕流有三个特征尺度,即横向分离或转捩流动有三个不同的尺度。研究表明,多尺度特征是高超声速绕流有别于低速绕流最重要的特征,也是高超声速飞行器气动力出现强烈非线性的根本原因之一。
建立了这三个频率的余弦和形式的滚转非定常气动力模型。从滚转力矩建模值与相应气动数据的对比来看,数学模型捕捉了试验曲线的基本趋势,也涵盖了主要的量值范围,而且周期性的表达形式反映了横向力矩周期性的物理特征。初步认为本文建立的非定常滚转力矩数学模型是适当的。
[1] Nixon David,Rodman Laura C.A study of supermanuever aerodynamics[R].ADA 218378,1990.
[2] Tobak M,Chapman G T,Schiff L B.Mathematical modeling of the aerodynamic characteristics in flight dynamics[R].NASA TM-85880,1985.
[3] Tobak M,Chapman G T,Uenal A.Modeling aerodynamic discontinuities and the onset of chaos in flight dynamical systems[R].NASA TM-89420,1986.
[4] Gupta N K,Iliff K W.Identification of integro-differential systems for application to unsteady aerodynamics and aeroelasticity[R].AIAA 85-1763,1985.
[5] Gupta N K,Iliff K W.Identification of unsteady aerodynamics and aeroelastic integro-differential systems[R].NASA TM-86749,1985.
[6] Bhaskar T G,Devi J V.Nonuniform stability and boundedness criteria for set differential equations[J].Applicable Analysis,2005,84 (2):131-142.
[7] Bhaskar T G,Devi J V.Stability criteria for set differential equations[J].Mathematical and Computer Modelling,2005,41(1):1371-1378.
[8] Lakshmikantham V,Bhaskar T G,Devi J V.Theory of set differential equations in metric spaces[M].Cambridge Scientific Publisher,2006:56-122.
[9] Feng Pan,Tao Cai,Jie Chen,et al.The stability analysis of particle swarm optimization without lipschitz condition constraint[J].Control Theory and Application,2004,1(2):46-57.
[10]Shi Zhiwei,Ni Fangyuan,Chen Yongliang,The state-space models based on two-step linear regression method[J].Acta Aerodynamica Sinica,2013,31(6):699-703.(in Chinese)
史志伟,倪芳原,陈永亮.基于两步线性回归的状态空间模型建立与验证[J].空气动力学学报,2013,31(6):699-703.
[11]Sun Haisheng,Zhang Haiyou,Liu Zhitao.Comparative evaluation of unsteady aerodynamics modeling approaches at high angle of attack[J].Acta Aerodynamica Sinica,2011,29(6):733-737.(in Chinese)
孙海生,张海酉,刘志涛.大迎角非定常气动力建模方法研究[J].空气动力学学报,2011,29(6):733-737.
[12]Yang Meng,Huang Da.The effects of variables on unsteady aerodynamic modeling[J].Acta Aerodynamica Sinica,2011,29(3): 355-359.(in Chinese)
杨勐,黄达,建模变量对非定常空气动力数学模型的影响[J].空气动力学学报,2011,29(3):355-359.
[13]Shi Zhiwei,Wang Zhenghua,Li Juncheng.The research of RBFNN in modeling of nonlinear unsteady aerodynamics[J].Acta Aerodynamica Sinica,2012,30(1):108-112.(in Chinese)
史志伟,王峥华,李俊成.径向基神经网络在非线性非定常气动力建模中的应用研究[J].空气动力学学报,2012,30(1):108-112.
[14]Shi Zhiwei,Wu Genxing,Huang Da.The validation of unsteady aerodynamic model based on the high amplitude harmonic rolling motion test[J].Acta Aerodynamica Sinica,2010,28(6):650-654.(in Chinese)
史志伟,吴根兴,黄达,基于大振幅谐波运动的非定常气动模型风洞实验验证[J].空气动力学学报,2010,28(6):650-654.
[15]Kumar R,Ganguli R,Omkar S N,et al.Rotorcraft parameter estimation from real time flight data using radial basis function networks[J].Journal of Aircraft,2008,45(1):333-341.
[16]Xia Y S,Feng G,Wang J.A novel recurrent neural network for solving nonlinear optimization problems with inequality constraints[J].IEEE Trans on Neural Networks,2008,19(8):1340-1353.
[17]Peyada N K,Ghosh A K.Longitudinal aerodynamic parameter estimation using neural network and Gauss Newton method[J].Journal of Aerospace Sciences and Technology,2009,61(2):295-304.
[18]Singh S,Ghosh A K.Parameter estimation from flight data of a missile using maximum likelihood and neural network method[C]// 2006 AIAA Flight Mechanics Conference and Exhibit,2006:21-24.
[19] Malmathanraj R,Thamarai Selvi S E.Prediction of aerodynamic characteristics using neural networks[J].Asian Journal of Information Technology,2008,7(1):19-26.
[20]蔡金狮.动力学系统辨识与建模[M].北京:国防工业出版社,1991.
[21]Klein V,Batterson J G,Murphy P C.Determination of airplane model structure from flight data by using modified stepwise regression[R].NASA TP-1916,1981.
[22]Klein V,Batterson J G.Determination of airplane model structure from flight data using splines and stepwise regression[R].NASA TP-2126,1983.
[23]Librescu L,Marzocca P,Silva W A,et al.Supersonic/hypersonic flutter and postflutter of geometrically imperfect circular cylindrical panels[J].Journal of Spacecraft and Rockets,2002,39(5):802-812.
[24]Chaitanya V S K.Stability analysis of structurally unstable man-machine system involving time delays[J].Nonlinear Analysis:Real Word Applications,2005,6(5):845-857.
[25]Hassard B,Kazarinoff N,Wan Y H.Theory and application of hopf bifurcation[M].Cambridge:Cambridge University Press,1981: 14-35.
[26]李周复,主编.风洞特种试验技术[M].北京:航空工业出版社,2010.
Non-steady roll moment modeling for hypersonic lifting configuration
Gao Qing,Li Jianhua*,Li Qian
(China Academy of Aerospace Aerodynamic,Beijing 100074,China)
Thorough study of lateral stability of hypersonic lifting aircrafts needs exact expression of aerodynamic roll moment.Spectrum analysis is carried out using roll free-oscillation wind-tunnel test data,and a mathematical model of roll moment is proposed as an expression by the sum of the cosine of the main frequencies from spectrum analysis.The roll test curves of hypersonic lifting model present non-linearity,non-steady and periodical characteristics,and the results of spectrum analysis of roll vibration data under several different flow conditions show that they share three main vibration frequencies apart from the mechanical vibration frequency,which indicates that there are three scales of lateral separation or transition in the flow field.Comparison of the mathematical model of roll moment constructed with the corresponding aerodynamic test data indicates,this model can capture the primary tendency of test curves,and cover the main magnitude domain of roll aerodynamic moment.The mathematical model gives prominence to the multi-scale and periodical characteristics of lateral flow field of hypersonic lifting model.
lifting-configuration;hypersonic;roll moment;non-steady aerodynamic;aerodynamic modeling
V211.3;O177.7
A
10.7638/kqdlxxb-2013.0061
0258-1825(2015)03-0392-05
2013-06-04;
2013-10-16
高清(1983-),女,山东曹县人,博士,高级工程师,研究方向:高超声速空气动力学和飞行力学.E-mail:1034505942@qq.com
李建华*(1977-),男,江西广昌人,高级工程师,研究方向:飞行器总体设计和气动布局设计.E-mail:ssanliren@126.com
高清,李建华,李潜.升力体高超声速飞行器非定常滚转力矩建模研究[J].空气动力学学报,2015,33(3):392-396.
10.7638/kqdlxxb-2013.0061 Gao Q,Li J H,Li Q.Non-steady roll moment modeling for hypersonic lifting configuration[J].Acta Aerodynamica Sinica,2015,33(3):392-396.

