差速驱动六轮导引车运动轨迹分析

暴海宁 宋 科 黎 原 冯艳丽 赵永亮 谭 旭

(中国航天科技集团第九研究院第十六研究所 西安 710100)

0 引言

AGV 是Automatic Guided Vehicles 的简称，属于轮式移动机器人(WMR——Wheeled Mobile Robot)的一种。根据美国物流协会定义，AGV 是指装备有电磁或光学自动导引装置，能够沿规定的导引路径行驶，具有安全保护以及各种移载功能的运输车。AGV 涉及机械、电子、光学、计算机等多个领域，广泛应用于自动化物流系统中［1］。AGV 导引车的核心技术主要包括导引技术、导引控制避障技术和路径规划技术等，而路径规划则是以上核心技术的基础性工作。优化路径规划可以在降低AGV 计算的复杂程度的同时，增加AGV 工作过程中的可靠性。AGV 运动的核心是驱动单元，由直流伺服电机，磁导引传感器，传动机构等组成。驱动单元通过前后端的磁导引传感器获取实时位置的引导信息，即驱动模块与磁导引条的角度和位置偏差，通过微调跟踪铺设的磁条路径行驶。同时磁导航因其铺设成本低，路径易于改变或扩充，差速驱动磁导航成为AGV 工业应用的一个重要方向值。文献［2-3］基于全局运动学建模算法在路径复杂时适应程度不高。文献［4-5］研究的AGV 为驱动模块与承载模块刚性连接的传统模型，驱动轮同时也是承载轮，导致在负载较大时对AGV 的路径跟踪控制难度加大。

本文讨论的CASC-远望号AGV 的牵引车驱动部分沿用差速驱动，其驱动模型如图1所示。本体采用六轮车型结构，牵引驱动模块安装在车体下部，驱动模块上部与车体柔性连接，下部跟踪预先铺设的的磁条行驶。车体前部两个从动万向轮起承重作用，车体后部两个从动固定轮起承重和防止摇摆作用。依靠电机调速使两驱动轮产生不同的线速度速度来实现转向。文章在分析AGV 牵引车系统结构及运动原理的基础上，描述了差速驱动AGV 牵引车车轮轨迹，并进行仿真验证，研究了六轮AGV 行驶路径情况。

图1 AGV 差速驱动模型

1 AGV 运动学分析

为了便于分析及建立CASC-远望号AGV 运动方程，本文做出如下假设:整个AGV 车体关于其纵轴对称;AGV 车体及所有车轮均为刚体;车轮在轨道平面做纯滚动，无打滑，且所有车轮始终与地面保持接触状态。

AGV 车体的运动由直线运动和曲线运动两部分构成，直线运动作为主要工作状态，要求平稳可靠;曲线运动即AGV 的转弯过程，作为辅助工作状态，要求快速稳定。在生产中，直行过程AGV 可以通过磁导航传感器实现微调，用RFID 标签实现工作过程中的路径选择。

1.1 AGV 直行及微调过程分析:

本文中AGV 为差速驱动，E、F 为驱动轮，前轮A、B 为万向轮，后轮C、D 为固定轮。在导引车行进过程中任取一点，其位置示意图如图2所示:

:AGV 行驶速度;

α:车体中心线与x 轴的正向夹角，即AGV 的方位角;

β:驱动轮EF 与车体中心线的夹角，即AGV 的转向角;

γ:驱动轮行进方向与x 轴正向夹角;

H:AGV 的轴距

L:AGV 前后轮与驱动轮之间的轮距

G:后轮CD 轴线的中心

图2 AGV 导引车运动模型

当前位置，AGV 的速度瞬心为P 点，在直线CD 与方向垂直的直线交点，根据图2所示的几何关系，有

令驱动轮的转向角速度为ωA，则其与车体中心线夹角为

AGV 作为刚体相对于瞬心P 的角速度ω 为:

综合上式可知:

此时车体的中心线与X 轴正向夹角为:

根据几何关系，由图可知，前轮与X 轴正向夹角为:

AGV 运动速度在X，Y 轴方向上的分量:

对速度进行积分可以得到驱动轮中心点J 的坐标方程为:

由式8、式9 可知:

将式6，式7 带入可得:

根据图示的几何关系，可以得到前后轮中心点的G 点，K 点的坐标方程为:

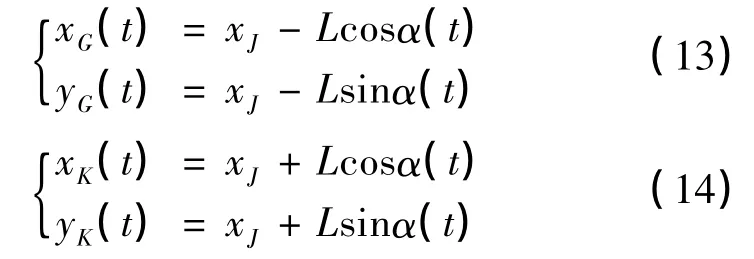
上式即为AGV 运动过程中的速度与轨迹的一般方程。其中四个轮子的轨迹方程为:

1.2 AGV 转弯过程分析

若AGV 在t0时刻沿直线L1的方向行驶，通过转弯过程，AGV 可以平稳的行驶到直线L2的方向上，如图所示。令直线L1、L2的方程为:

图3 AGV 转弯过程示意图

其中α0、αn，b1、b2分别为L1、L2的方位角和截距。鉴于AGV 是通过一段圆弧来完成它的平稳的转弯过程，应确保该圆弧能够与初始方向直线和目标方向直线均相切。针对已知的运动轨迹，其行驶直线、目标直线和转弯半径就是确定的。为了提高车体反应速度，减少计算量，在工程实际控制中，采用RFID 标签选择路径，即在进入转弯起点处之前增加RFID 电子标签，设置左右优先权限，从而实现顺时针、逆时针转弯选择问题。AGV 自身的转弯过程只需知道其驶入弯道过程的起始点J 的坐标。当AGV 分别采用顺时针和逆时针来实现转弯过程时，其进入弯道的起始点是不同的，因此首先应该根据电子标签的设定，读取左右优先级状态再判断AGV 该采用何种转弯方式，然后运用数学计算推导得出转弯圆弧轨道的圆心坐标O。为了计算O 点的坐标，在L1和L2的基础上构建参考平行直线L11和L22，并计算出L11和L22的交点，即O 点的坐标:

过圆心O 点做垂直于L1的直线，其与L1的交点E 点即为AGV 驶入弯道过程的起始点，通过联立直线OE 和L1的方程，可以得到两条直线的交点E点的坐标，即AGV 驶入弯道的起始点为:

类似可知，在α0或者αn等于nπ/2(n 为任意整数)的情况下也可以得到AGV 驶入弯道的起始点。

2 运动仿真及实验验证

本文选择使用Maple 软件对AGV 运动过程进行运动仿真。在已经得到AGV 驶入弯道起始点的基础上，采用积分方法可以得到驱动单元与车体的夹角，即导向角的大小。同时根据AGV 在运动过程中速度方程和预定轨道的方程就可以对AGV 在弯道行驶过程进行仿真验证。

结合实际场地布置及使用功能要求，分别取直线L1、L2的截距b1=0 、b2=0，AGV 的行驶速度v=1m/s，转弯半径r=1m，轴距0.6m，转向角初始值α0=π/6，αn=5π/6，β0=0 经过Maple 仿真，AGV 的转向角β 的仿真结果及计算对比如图4所示。其中虚线为仿真结果，实线为计算结果。实验结果表明，该模型与AGV 运动实验结果类似，证明所建立的模型与AGV 实际运动情况一致。

图4 AGV 转向角β 误差对比

在模型正确的基础上，保持初始值不变，可以得到车体中心线与X 轴正向夹角α 和前轮与车体中心线夹角β 的曲线。

图5 AGV 方位角α 和导向角β 曲线

由图5 可以看到导向角β 曲线变化可以分为三个过程:

1)从0s 到2s 的过程中，导向角β 由0 开始逐渐增大，方位角α 也在随之逐渐增加，AGV 磁导航装置进入圆弧轨道，开始转弯阶段。

2)从2s 到9s 的过程中，β 保持不变，由公式(5)分析可知，此时AGV 以恒定的角速度ωA行驶在预定的轨道上，AGV 进入了稳定的转弯阶段。

3)从9s 到14s 阶段，β 逐渐减小直至最终到0的过程中，AGV 沿着轨迹逐渐驶出弯道，方位角α持续增加。当β=0 时，α=αn，AGV 平稳驶出圆弧轨道，结束转弯阶段。

为了了解AGV 整体在预定轨道上的行驶状况，研究轨迹误差，对AGV 整车进行运动过程分析，得到前后两对承重轮及驱动轮的运动轨迹方程，由图6 可知，AGV 能能够很好的完成整个转弯过程，整体运行平稳，跟踪路径准确。

图6 AGV 整体转弯过程轨迹

3 总结

本文对差速驱动六轮导引车进行运动过程分析，建立了车体与所跟踪路径的位置关系模型，计算出AGV 运动过程中轨迹与运动的一般方程，分析了差速驱动装置工作中车体驱动轮和承重轮的轨迹问题。然后对AGV 的转弯过程进行了分析，并根据车体的几何尺寸及预定轨道的半径，计算出了AGV 开始转弯过程的起始点，并且用MAPLE 进行编程，仿真得到AGV 在转弯过程中的方位角和导向角的变化曲线以及六个轮子的轨迹。实验中车体位姿验证了模型的正确性，为六轮自动导引车行驶路径提供了可参考的模型和算法，AGV 车体行驶轨迹为车体结构设计和磁导航轨道的铺设提供一定的理论支持。

［1］武星，楼佩煌，唐敦兵.自动导引车路径跟踪和伺服控制的混合运动控制［J］.机械工程学报，2011，47(3):43-48.

［2］沈颖.激光导引AGV 车载控制系统研究［D］.合肥:合肥工业大学.2007.

［3］钱晓明，吴斌武星，楼佩煌.潜入牵引式自动导引车运动特性分析［J］.农业机械学报，2014，4(2):29-30.

［4］刘沙沙，魏生民，薛瀛，汪焰恩。基于视觉引导AGV 路径跟踪模糊控制研究［J］.机床与液压2009，8:32-86.

［5］孟琦，金亚萍，耿牛牛，史伟伟，许鹏鹏.基于磁线导引的双转向架驱动AGV 应用研究［J］制造业自动化.2014，8:40-44.

［6］周驰东，楼佩煌，王辉，张炯.移载式磁导航AGV 关键技术研究［J］.工业控制计算机.2012，1:22-25

［7］贺长林，史恩秀.基于双目立体视觉和侧向路径的AGV 导航技术研究［D］.西安:西安理工大学.2008.