四阶幻方的一个构造方法①

智 婕，李旭东

(1.兰州商学院信息工程学院，甘肃 兰州730000;2.兰州城市学院数学学院，甘肃 兰州730070)

0 引 言

幻方，又称纵横图，在n×n 的方格里既不重复又无遗漏地添上1，2，3，…，n2这n2个连续自然数，每数占一格，使每行、每列、每条对角线上的n 个数的和都相等，这样的数表称为n 阶幻方.著名的九宫图即三阶幻方.幻方因其趣味性和益智性，引起了古往今来许多人的迷恋.我国对幻方的研究可以追溯到公元前四世纪，而宋代杨辉、明朝程大位、清朝张潮、保其寿等都做了深入的研究，幻方是我国丰富的文化遗产之一.国外著名科学家欧拉、富兰克林等也都喜欢研究幻方.近代的科学研究发现，幻方同现代数学群论、组合分析等有关.随着电子计算机技术的迅速发展，幻方已在程序设计、图论、人工智能、博弈论、组合分析、实验设计、工艺美术等方面得到了新的应用.

幻方在数学王国里扮演着一个神秘的角色，从小学生的智力测验题到中学生的课外思考题，无处不有幻方的谜影.至今日幻方仍然是一个古老有趣的问题.本文将给出四阶幻方的一个简便的构造方法.为讨论方便，以下将幻方表示成矩阵的形式.

1 主要结果

定理 任取数码1，2，3，4 的一个4 级排列放在第4 行，通过+2 置换得第1 行，取第1 行的倒排列放在第2 行、第4 行的倒排列放在第3 行，这样便得到一个4 阶方阵A=(aij)4，将A 旋转90 度或－90 度得到方阵B=(bij)4，做方阵A°B=(xij)4，其中xij=4(aij－1)+bij，i，j=1，2，3，4，则A°B 就是一个幻和为34 的4 阶幻方，同理B°A 也是幻和为34的4 阶幻方.

2 定理的证明

设a，b，c，d 是1，2，3，4 的任意一个4 级排列，将A 旋转90 度得到方阵记为B，将A 旋转－90 度得到方阵记为D，则需验证A°B，B°A，A°D，D°A 均为幻和是34 的4 阶幻方.事实上，由A，B，D 的构造过程知，

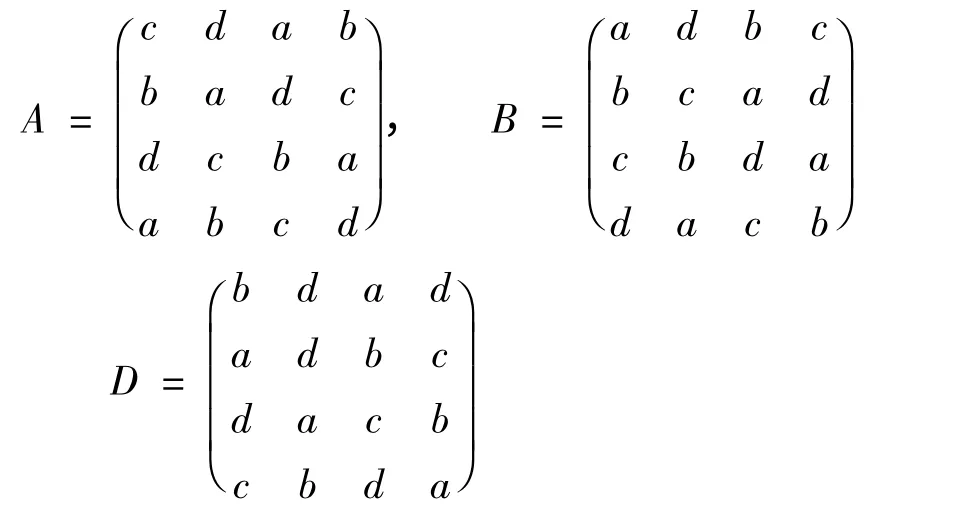
于是，

对这四个矩阵，容易验证，每行、每列以及每条长对角线上4 个数的和均为

即A°B，B°A，A°D，D°A 都是幻和为34 的4 阶幻方.

注:对每一个4 级排列，都可得到4 个4 阶幻方，因此运用以上方法对24 个4 级排列总共可得24×4=96 个4 阶幻方.

3 举 例［1］

已知幻方

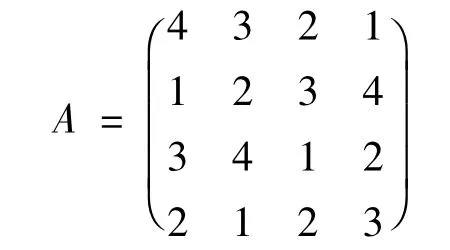
将A 旋转90 度得到方阵记为B，将A 旋转－90度得到方阵记为D，则

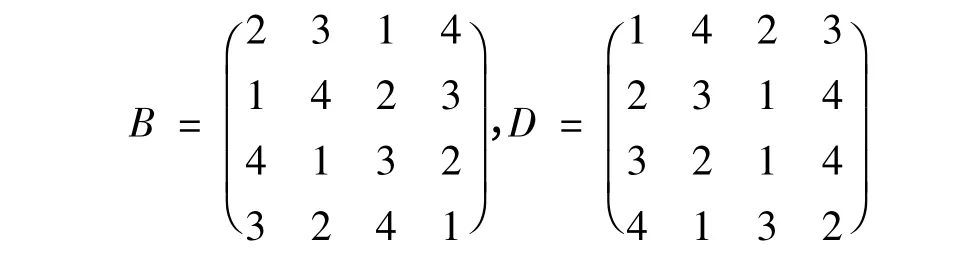
于是

是4 个幻和为34 的4 阶幻方.

又如取4 级排列为1243，则由定理知

将A 旋转90 度得到方阵记为B，将A 旋转－90度得到方阵记为D，则

于是

又是4 个幻和为34 的4 阶幻方.

［1］ 吴鹤龄.幻方及其他［M］.第2 版.北京:科学出版社，2004:149－150.

［2］ 唐编著.吴振奎、江常风审订.幻方与数阵趣谈［M］.北京:科学普及出版社，1985，6.