一种对称损失函数下几何分布参数的Bayes 估计①

徐瑞标

(武夷学院人文与教师教育学院，福建 武夷山354300)

0 引 言

在参数估计问题中，参数估计及其优良性一直是非常重要的研究课题.近年来用Bayes 方法取得了一些进展，自文献［1］中提出了多层先验分布的想法以来，韩明博士在文献［2］给出多层先验分布的构造方法及应用，多层Bayes 方法在参数估计上取得了一些进展.本文则是研究在一种对称损失函数下，几何分布参数的Bayes 估计、多层Bayes 估计，并讨论Bayes 估计的可容许性及置信下限等相关问题.

1 有关定义及引理

定义1［3］: 在伯努利试验中，若p 为每次试验成功的概率，如果进行了k+1 次试验，则前次k成功且第k+1 次不成功(或失败)的概率为:

其中，k=0，1，2，…0 ＜p ＜1，，称随机变量X 服从几何分布，其中参数p 为几何分布(1)的可靠度(或成功率).

定义2［4］: 设随机变量X 服从密度函数为f(x|θ)的分布，其中θ 为参数，如果δ 是θ 的判决空间中的一个估计，则对称损失函数为:

且L(θ，δ)关于参数θ 和估计量δ 是对称的，L(θ，δ)关于δ 是严凸的，并在δ=θ 处取得唯一的最小值.

定义3［5］: 设随机变量X 服从密度函数为f(x|θ)的分布，其中θ 为参数，参数δ 的先验分布为π(θ|a，b)，超参数a，b 服从密度函数π(a，b)的分布，则θ 的多层先验分布密度为:

θ 的多层后验分布密度为:

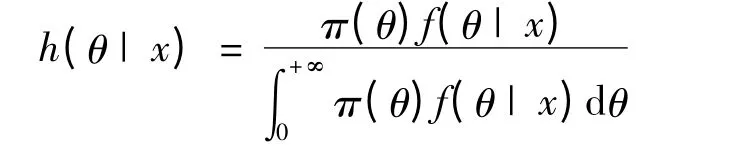
那么在对称损失函数(2)下，以π(θ)为先验分布密度的θ 的Bayes 估计称为多层Bayes 估计.

引理1［6］: 在对称损失函数(2)下，对任何先验分布π(θ)，θ 的Bayes 估计为:

并且如果δB(x)的Bayes 风险有限，则δB(x)是唯一的Bayes 估计.

引理2［7］: 在给定的Bayes决策问题中，假如对给定的先验分布π(θ)，θ 的Bayes 估计是唯一的，则δB(x)是可容许估计.

2 定理及证明

定理1: 对几何分布(1)，若p 的先验分布为共轭分布Beta 分布，即

则在对称损失函数(2)下几何分布参数p 的Bayes 估计为:

证明: 因为参数p 的后验分布由

所以由引理1 可得:

(证毕)

定理2: 对于几何分布(1)，如果参数p 的先验密度函数π(p|a，b)为Be(a，b)，超参数(a，b)服从密度为π(a，b)，(其中0 ＜b ＜1，1 ＜a ＜c，c 为常数)，则在对称损失函数(2)下参数p的多层Bayes 估计为:

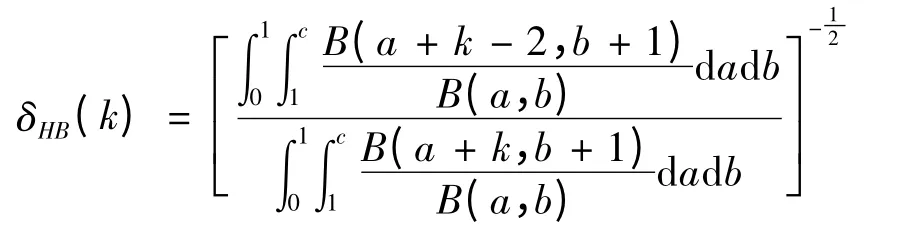
证明: 因为参数p 的多层先验密度函数为:

参数p 的多层后验密度函数为:

所以在对称损失函数(2)下，参数p 的多层Bayes 估计为:

(证毕)

定理3: 在对称损失函数(2)下几何分布参数p 的Bayes 估计

是可容许估计.

证明: 因为对称损失函数

δ 关于是严格凸函数，则其Bayes 估计必是唯一的，由引理2 可得Bayes 估计δB(k 许估计.

(证毕)

定理4: 对于几何分布(1)，给定参数p 的先验分布Be(a，b)，在对称损失函(2)下，参数p 的置信水平1－α 为的Bayes 置信下限θL满足:

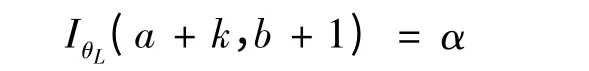
证明: 参数p 的置信水平为1－α 的Bayes 置信下限θL满足

则

(证毕)

［1］ Lindley D V，Smith A F M.Bayes Estimate for the Linear Model［J］.Roy.Statist.Soc.(Ser B)，1972，34:1－41.

［2］ 韩明.多层先验分布的构造及其应用［J］.运筹与管理，1997，6(3):31－40.

［3］ 韩明.二项分布可靠度的Bayes、多层Bayes 估计［J］.数理统计与应用概率，1996，11(3):232－239.

［3］ 复旦大学.概率论(第一册)［M］.北京:人民教育出版社，1979.

［4］ 王忠强，王德军.一种对称损失函数下正态总体刻度参数估计［J］.应用数学学报，2004，27(2):310－323.

［5］ 韩明.二项分布可靠度的Bayes、多层Bayes 估计［J］.数理统计与应用概率，1996，11(3):232－239.

［6］ 韦师.几种分布参数的E－Bayes 估计及其应用［D］.南宁:广西师范学院，2010.

［7］ 茆诗松.高等数理统计［M］.北京:高等教育出版社，1998:367－372.