矢跨比对雪荷载作用下双层柱面网壳静力性能的影响①

吴漪璘

(上海大学土木工程系，上海200072)

0 引 言

双层柱面网壳是由两个同心或不同心的单层网壳通过连接而成的曲面形网格结构，兼有杆系结构和薄壳结构的双重受力特性，是一种跨越空间较大，建筑造型优美，受力更为合理，便于工业化生产的典型的网壳结构，具有广泛的应用空间和研究领域［1］.

近年来，我国各地遭受不同程度的风雪灾害，导致大量建筑物的破坏甚至倒塌，造成了人员伤亡和经济损失.雪荷载是重要的结构设计指标，取值不当将影响结构的安全.双层柱面网壳屋面雪荷载的计算，应当重视风致积雪的飘移堆积效应［2～3］，即同时考虑积雪均匀和不均匀两种分布情况，两者的积雪分布系数均与矢跨比有关［4～6］.

本文在《空间网格结构技术规程》(JGJ7－2010)［7］建议参数的基础上，以正放四角锥双层柱面网壳为例［8］，系统研究了雪荷载作用下几种典型矢跨比网壳的静力性能，探讨了不同矢跨比对网壳杆件轴力、节点竖向位移、支座侧向反力、支座侧向位移等静力响应的影响规律，并提出了网壳选型和设计的建议［9～10］.

1 计算模型

结构的计算模型如图1 所示，矢高分别为13.5 m，10 m，8 m，6.5 m(即矢跨比1/3，1/4，1/5，1/6)，平面尺寸为40 m×40 m，网壳厚度为3 m.上弦层、下弦层X 方向杆件、所有腹杆均采用，上弦层及下弦层Y 方向杆件的截面配置情况如图1(b)和表1 所示.结构模型关于跨中对称.

恒载标准值:上弦0.5 kN/m2，下弦0.5 kN/m2;雪荷载标准值:0.65 kN/m2.风向与Y 轴方向相反，屋面积雪分布系数如图2 所示.

工况组合:(1)工况Ⅰ:1.2×恒载+1.4×均匀分布雪载

(2)工况Ⅱ:1.2×恒载+1.4×不均匀分布雪载

采用两纵边上弦节点支承，支座间距为4 m，支座X、Y 两向弹性约束，Z 向固定约束条件，其中弹性支承刚度:kN/mm.

表1 弦层Y 方向杆件的截面配置情况

2 参数分析

2.1 杆件轴力分布

工况Ⅰ下，网壳模型两个半跨结构的内力关于跨中对称.工况Ⅱ下，背风面的半跨内力明显大于迎风面的半跨.两种分布情况下，杆件轴力

均由端边跨向中间跨递增，由支座向跨中递增，因此杆件最大轴力发生在1－1 剖面，如图1(a)所示.1－1 剖面杆件编号如图3 所示，弦层杆件轴力见表2 和图4，其中表2 仅列出图3 中处于背风面的左半跨杆件轴力.

图1 双层柱面网壳结构模型

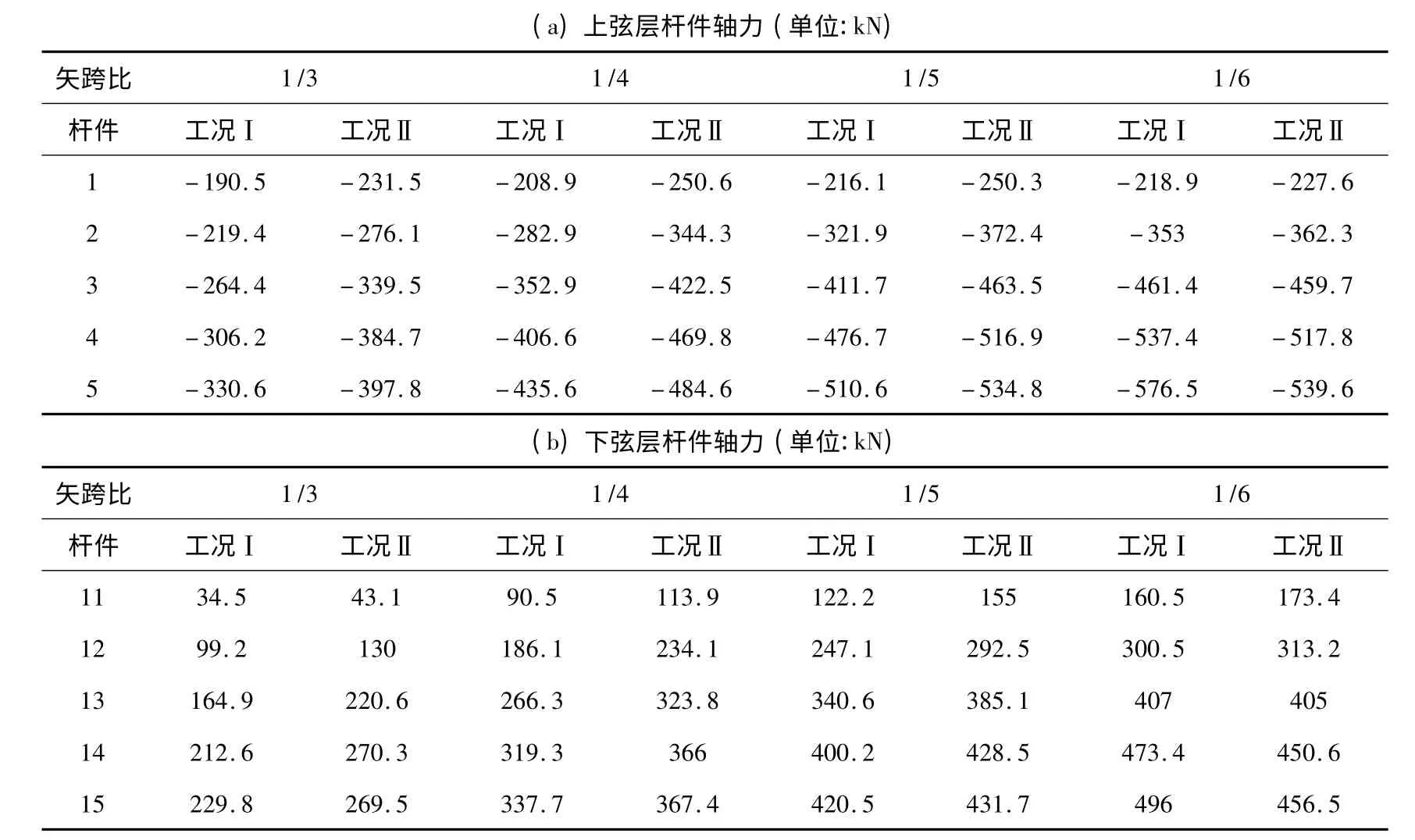
表2 1－1 剖面杆件轴力

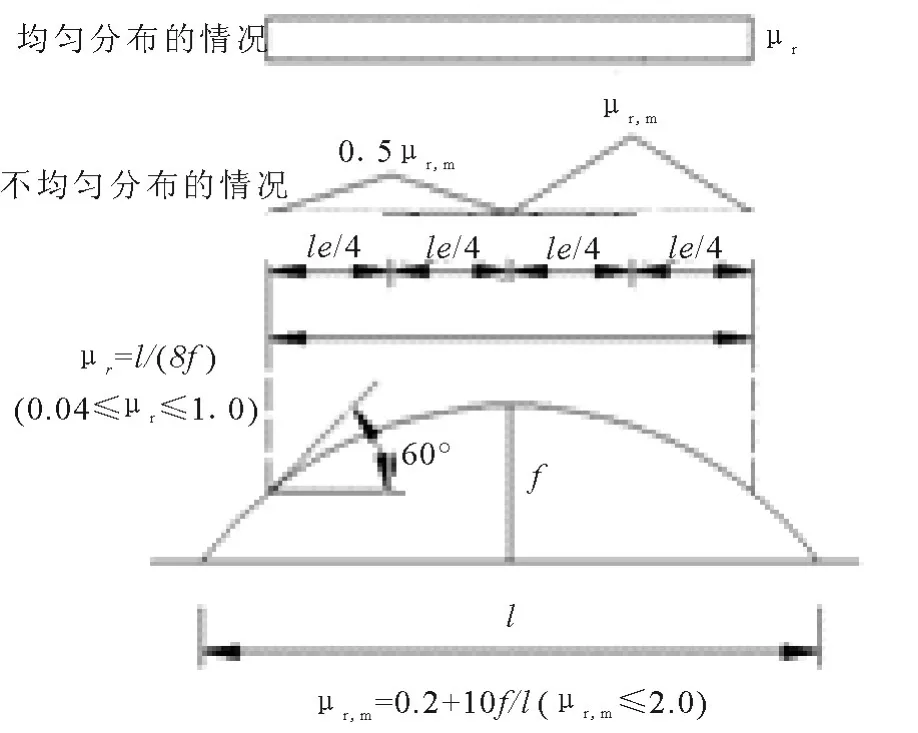
图2 屋面积雪分布系数

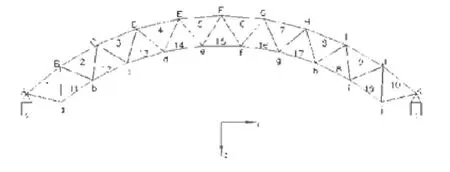
图3 1－1 剖面杆件、节点标号

工况Ⅰ下，1－1 剖面两弦层杆件轴力均随矢跨比减小而增大，支座附近杆件轴力的变化较为明显，跨中杆件轴力变化较不明显.上弦支座附近最大值约为最小值的1.74 倍，跨中附近最大值约为最小值的1.15 倍.下弦支座附近最大值约为最小值的4.65 倍，跨中附近最大值约为最小值的2.16倍.工况Ⅱ下，上弦层支座附近杆件轴力随矢跨比减小先增大后减小，但数值变化不大，而跨中附近则单调递增，最大值约为最小值的1.36 倍.下弦层杆件轴力随矢跨比减小迅速增大，支座附近杆件轴力增幅较大，增幅达378%，跨中杆件轴力增幅稍小，增幅为69%.杆件在两种工况下的轴力之比(工况Ⅱ/工况Ⅰ)随矢跨比减小而增大，仅当矢跨比为1/6 时，该比值小于1.

2.2 节点竖向位移

类似杆件轴力分布情况，网壳节点的最大竖向位移同样发生在1－1 剖面，节点编号如图3 所示.各节点的竖向位移情况见表3 和图5，其中表3 仅列出图3 中左半跨的节点竖向位移.

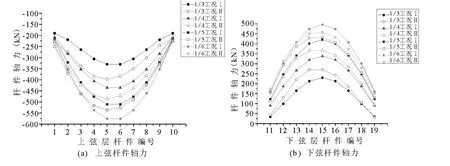
图4 1－1 剖面上下弦杆件轴力图

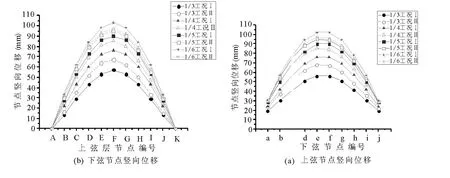
图5 1－1 剖面节点竖向位移

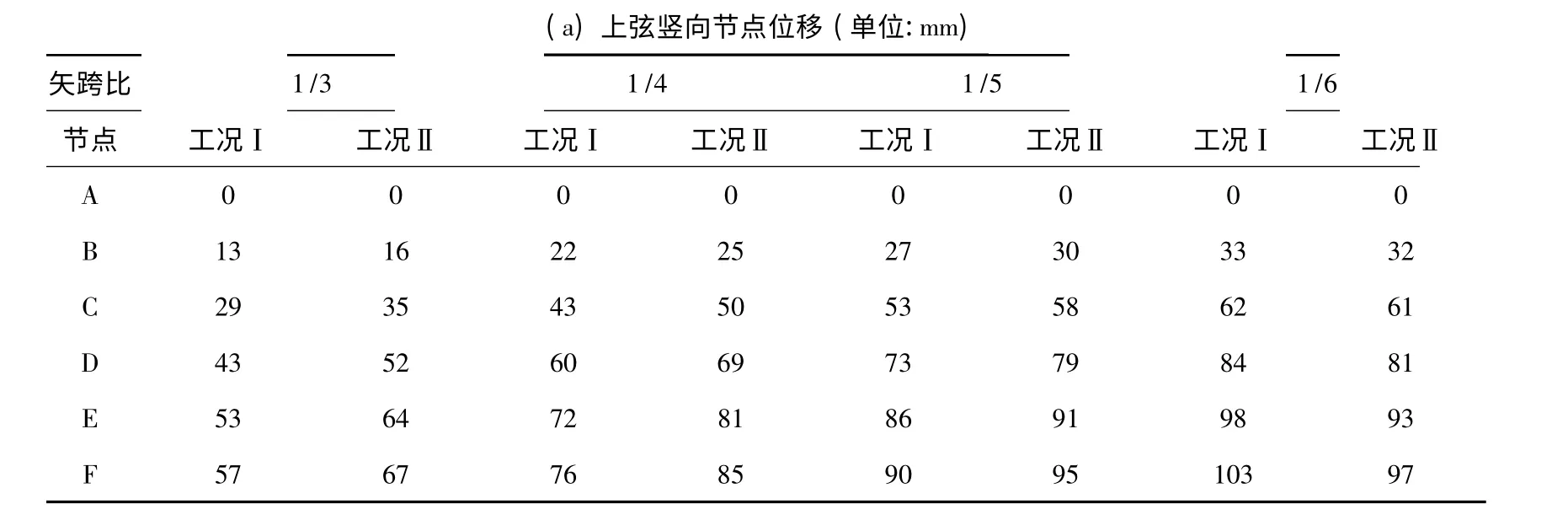
表3 1－1 剖面节点竖向位移

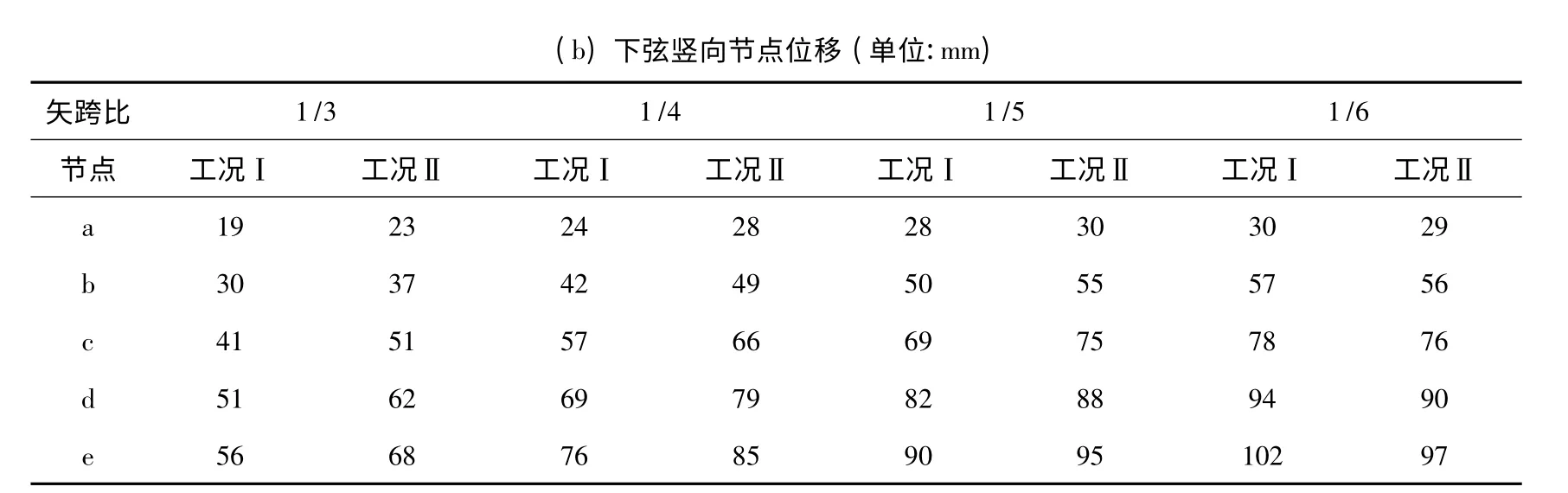
(b)下弦竖向节点位移(单位:mm)矢跨比1/3 1/4 1/5 1/6节点 工况Ⅰ 工况Ⅱ 工况Ⅰ 工况Ⅱ 工况Ⅰ 工况Ⅱ 工况Ⅰ 工况Ⅱa 19 23 24 28 28 30 30 29 b 30 37 42 49 50 55 57 56 c 41 51 57 66 69 75 78 76 d 51 62 69 79 82 88 94 90 e 56 68 76 85 90 95 102 97

工况Ⅰ下，两弦层节点竖向位移均随矢跨比减小而增大，上弦跨中节点竖向位移最大差值为46 mm，增幅为81%，下弦跨中节点的竖向位移最大差值为47 mm，增幅为82%.工况Ⅱ下，两弦层节点竖向位移同样随矢跨比减小而增大，上弦跨中节点竖向位移最大差值为30 mm，增幅为45%，下弦节点竖向位移最大差值为29 mm，增幅为43%.可见，矢跨比对雪荷载均匀分布情况下网壳的节点竖向位移影响更大.仅在矢跨比为1/6 时，工况Ⅱ下网壳的节点竖向位移小于工况Ⅰ，且前者与后者的比值随矢跨比减小而减小.

2.3 支座侧向反力

由于拱形结构的存在，支座处水平推力较大，一般会给下部支承结构的设计带来困难，因此解决水平推力过大成为拱形结构设计的一个关键点.各支座编号见图1(a)，选取图3 中左半跨的支座，考虑到对称性，对1－6 号支座的侧向反力进行分析，各支座侧向反力见表4 和图6，图6 中各支座的侧向反力值均取绝对值.

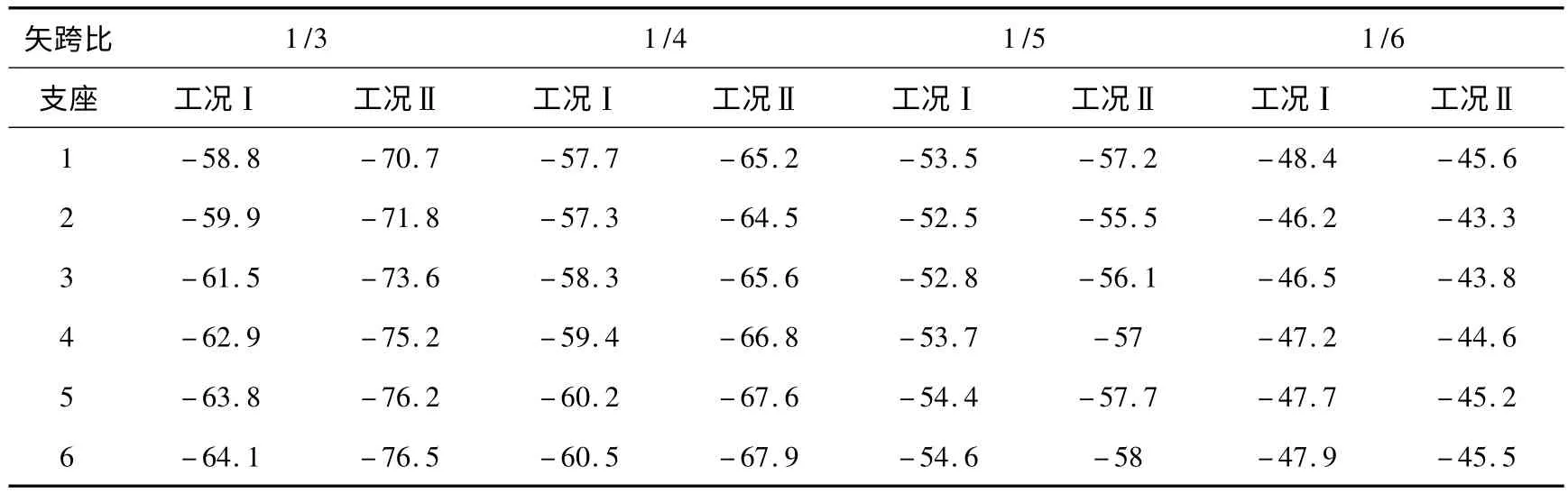
表4 支座侧向反力(单位:kN)

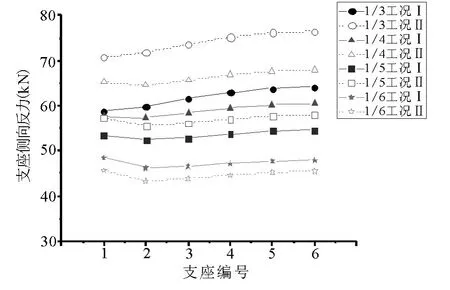
图6 支座侧向反力图

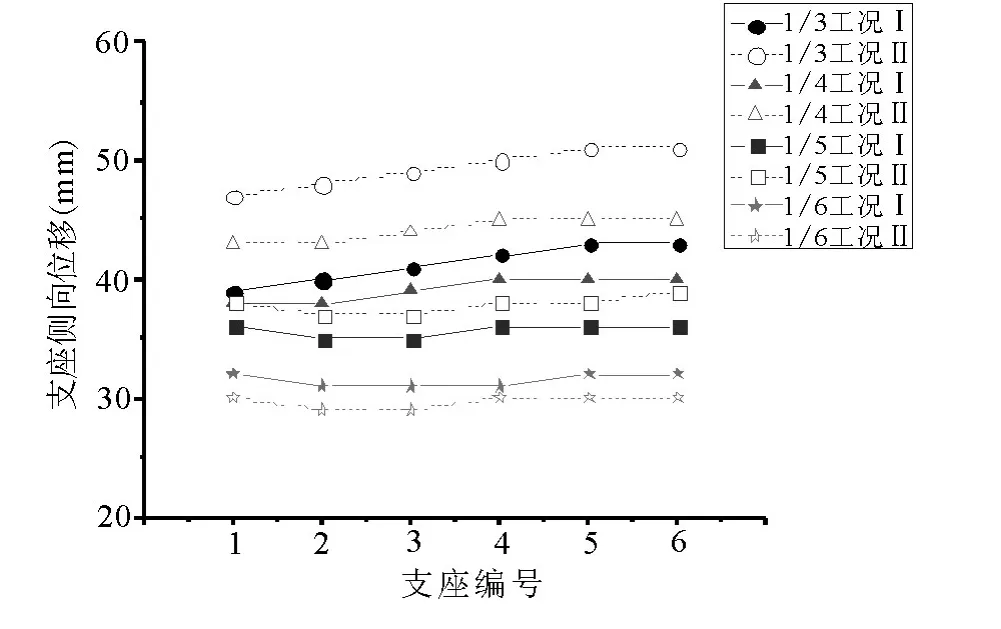
图7 支座侧向位移

工况Ⅰ下，支座的侧向反力随矢跨比减小而减小，最大值约为最小值的1.34 倍.工况Ⅱ下，支座的侧向反力随矢跨比减小的变化趋势与工况Ⅰ相同，但递减幅度更为明显，最大值约为最小值的1.68 倍.仅在矢跨比为1/6 时，工况Ⅱ的支座侧向反力小于工况Ⅰ，其他情况下工况Ⅱ下的支座侧向反力均大于工况Ⅰ，两种工况下支座侧向反力之比(工况Ⅱ/工况Ⅰ)随矢跨比减小而减小，在矢跨比取1/6 时小于1.仅在矢跨比为1/3 时，支座侧向反力随支座编号增大而增大，即支座侧向反力从端边跨向中间跨递增，增幅达8.2%，其他情况下，支座侧向反力随支座编号增大出现先减小后增大的现象，矢跨比越小其增幅越小，各支座侧向反力值趋于平均.当矢跨比一定时，各支座在两种工况下的侧向反力之差趋于一致，分别约为12.2 kN，7.5 kN，3.3 kN 和－3.3 kN，且该差值随矢跨比减小而减小.

2.4 支座侧向位移

拱形结构除支座水平推力外，支座的水平侧移值也是结构设计的重要参考依据.取图1(a)中1－6 号支座的侧向位移进行分析，结果如表5 所示

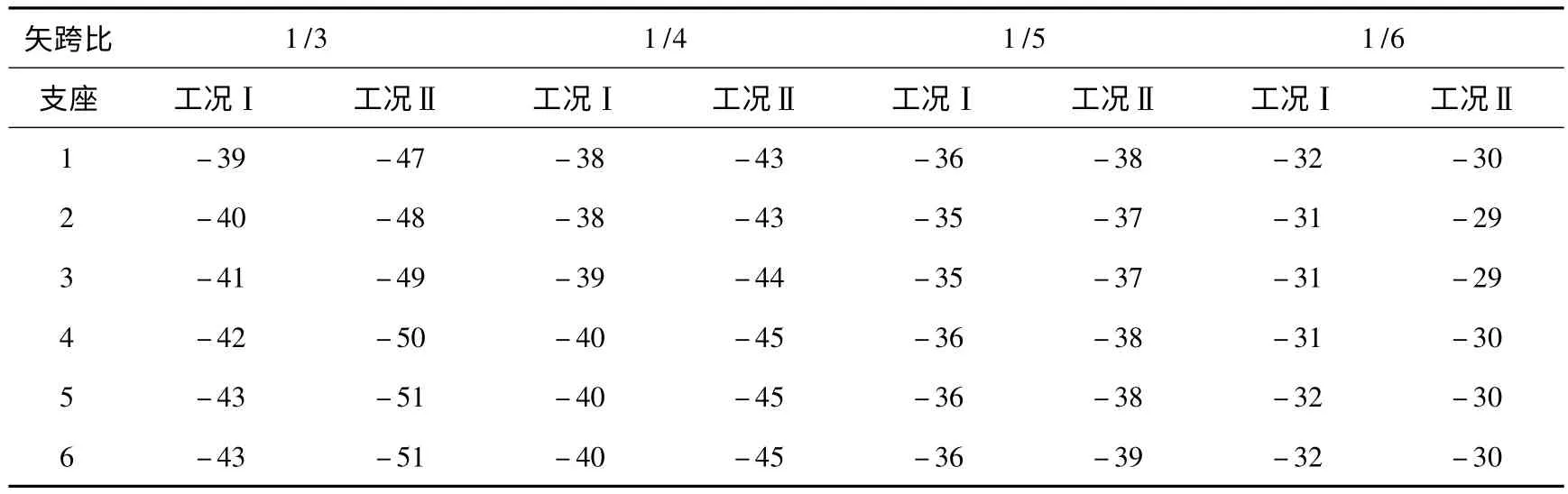
表5 支座侧向位移(单位:mm)

工况Ⅰ下，支座的侧向位移随矢跨比减小而减小，同一支座最大侧向位移之差为11 mm，减幅为25.4%.工况Ⅱ下，支座侧向位移的变化趋势同工况Ⅰ，同一支座最大侧向位移之差为20 mm，减幅为41.2%.仅在矢跨比为1/6 时，工况Ⅱ下支座的侧向位移小于工况Ⅰ，且前者与后者的比值随矢跨比减小而减小.当矢跨比较大，取1/3、1/4 时，支座侧向位移随支座编号增大总体呈递增趋势，即支座侧向位移从端边跨向中间跨递增，增幅达8.5%，且同矢跨比下各支座在两种工况下的侧向位移之差趋于一致，分别为8 mm 和5 mm.然而当矢跨比较小，取1/5、1/6 的情况下，各支座的侧向位移差别不大，并随支座编号增大呈先减后增趋势，此外同矢跨比下各支座在两种工况下的侧向反力之差并不一致.

3 结 论

(1)网壳的杆件内力随矢跨比减小而增大，下弦层均比上弦层对矢跨比变化更为敏感，下弦层支座附近杆件均较跨中杆件更为敏感.积雪均匀分布情况下，上弦层支座附近杆件较跨中杆件更为敏感;积雪均匀分布情况下，上弦层支座附近轴力对矢跨比变化不敏感，跨中杆件对矢跨比变化比较敏感.因此，进行强降雪地区网壳结构设计时，应当重视风致积雪飘移堆积效应，特别注意下弦层支座附近杆件的内力变化.

(2)网壳节点竖向位移均随着矢跨比减小而增大，相同雪荷载分布情况上下弦节点竖向位移对矢跨比变化的敏感程度相同，但在雪荷载均匀分布情况下节点竖向位移对矢跨比的变化更为敏感.网壳选型时，矢跨比较小会引起较大的竖向位移，可能导致屋面结构挠度过大，影响正常使用，应当予以重视.

(3)网壳的支座侧向反力随矢跨比减小而减小.矢跨比较大时，网壳的支座侧向反力在雪荷载不同分布情况下的差值较大，中间跨支座的侧向反力明显大于端边跨;矢跨比较小时，各支座反力受积雪分布情况影响较小，数值比较接近.网壳选型时采用较大矢跨比，会产生较大的支座侧向反力，应注重支承结构材料特性、截面尺寸及经济性的综合考虑.

(4)网壳的支座侧向位移随矢跨比减小而减小.矢跨比较大时，网壳的支座侧向位移从端边跨向中间跨递增明显，在雪荷载不同分布情况下支座侧向位移差值较大;矢跨比较小时，支座侧向位移由端边跨向中间跨先减后增，但变化幅度不大，受积雪分布情况影响较小.网壳选型时采用较大矢跨比，会产生较大的支座侧向位移，应重视下部支承结构应选用侧向刚度，避免产生过大侧移.

［1］ 张毅刚，薛素铎，杨庆山，等.大跨空间结构［M］.北京:机械工业出版社，2014.

［2］ 周毅，顾明，李雪峰.大跨度屋盖表面风致雪压分布规律研究［J］.建筑结构学报，2008，29(2):7－12.

［3］ 周晅毅，顾明.风致积雪漂移堆积效应的研究进展［J］.工程力学，2008，25(7):5－17.

［4］ GB50009－2012.建筑结构荷载规范［S］.北京:中国建筑工业出版社，2012.

［5］ 金新阳.建筑结构荷载规范理解与应用［M］.北京:中国建筑工业出版社，2013.

［6］ 范峰，莫华美，洪汉平.中、美、加、欧屋面雪荷载规范对比［J］.哈尔滨工业大学学报，2011，43(12):18－22.

［7］ JGJ7－2010.空间网格结构技术规程［S］.北京:中国建筑工业出版社，2010.

［8］ 赵鹏飞.空间网格结构技术规程理解与应用［M］.北京:中国建筑工业出版社，2013.

［9］ 董继斌.双层柱面网壳的选型与设计［J］.钢结构，1997，1(12):49－55.

［10］ 董继斌，刘晓勇.双层柱面网壳设计研究［J］.建筑结构，1999，6(6):25－29.