车辆主动悬架的遗传粒子群LQG控制方法*

陈 双，宗长富

(1.辽宁工业大学汽车与交通工程学院，锦州 121000；2.吉林大学,汽车仿真与控制国家重点实验室，长春 130022)



2015034

车辆主动悬架的遗传粒子群LQG控制方法*

陈 双1，宗长富2

(1.辽宁工业大学汽车与交通工程学院，锦州 121000；2.吉林大学,汽车仿真与控制国家重点实验室，长春 130022)

针对LQG最优控制算法中权重系数依靠经验确定的不足，综合遗传算法和粒子群算法优点，将粒子群算法中粒子速度和位置的更新和遗传算法的选择、交叉与变异操作相结合，提出遗传粒子群LQG控制算法，以优化性能指标权重系数。建立2自由度1/4主动悬架车辆模型，利用Matlab/Simulink软件，对车辆悬架的遗传粒子群LQG控制进行仿真，并与传统LQG控制结果进行对比。结果表明，所提出的遗传粒子群LQG控制方法能同时改善汽车的平顺性和操纵稳定性。

车辆；主动悬架；LQG控制；遗传粒子群算法

前言

在设计主动悬架最优控制器时，通常情况下是根据系统物理过程和实践经验初步确定性能指标量的权重系数，并进行车辆模拟仿真[1-2]。如果仿真结果不理想，设计人员再根据响应量逐步调整权重系数，直到获得满意的输出响应量为止。这种依靠经验选择权重系数的方法需要设计人员对系统有非常充分的了解，需要大量的时间反复调试。目前，有些学者提出通过遗传算法优化得到权重系数，文献[3]中利用遗传算法，以系统瞬态响应为目标确定线性二次型最优控制加权阵。文献[4]中针对主动悬架最优控制，建立了一种基于遗传算法的线性二次型调节器，对性能指标车身垂向加速度、悬架动挠度和轮胎动变形权重系数进行寻优，增加了获得最优权重系数的可能性，取得了一定成果。

本文中提出一种基于遗传算法和粒子群算法混合优化的LQG最优控制方法，简称遗传粒子群LQG控制方法，其中，LQG算法用于设计悬架控制器，遗传粒子群算法用于悬架控制器中性能指标权重系数的优化。通过1/4车辆悬架控制的仿真，验证了控制方法的正确性和有效性。

1 1/4车辆悬架模型

本文中构建了一个主动悬架2自由度1/4车辆简化模型，即车身垂向运动和车轮垂向运动[5]2自由度模型，如图1所示。

由牛顿运动定理可得到振动系统的微分方程。

车身垂向运动：

(1)

车轮垂向运动：

(2)

式中：ms为车身质量，kg；muf为车轮质量，kg；Kf为弹簧等效静刚度，N/m；Ktf为轮胎垂向刚度，N/m；F为主动悬架力，N；Cf为减振器等效阻尼系数，N·s/m；zs为车身垂向位移，m；zu为车轮垂向位移，m；q为路面垂向位移，m。

2 遗传粒子群LQG控制器设计

车辆悬架LQG控制器中，性能指标权重系数的大小反映系统对不同性能指标的重视程度，直接影响控制器设计的好坏。遗传粒子群LQG的控制原理如图2所示。

2.1 悬架LQG控制器设计

(3)

其中：

取1/4车辆悬架LQG控制器性能指标函数JA为

ρ3(zu-zs)2+ρ4F2}dt

(4)

式中：ρ1为车身垂向加速度权重系数；ρ2为轮胎动载荷权重系数；ρ3为悬架动行程权重系数；ρ4为悬架控制力权重系数。

将式(4)整理成标准的二次型：

(5)

其中：

2.2 遗传粒子群优化算法

遗传算法和粒子群算法都是从需要解决问题空间中的多个点开始搜索，具有相同的寻优能力。虽然遗传算法比传统优化方法(如单点搜索方法)具有良好的收敛性，但由于遗传算法的局部搜索能力较差，导致单纯的遗传算法非常费时，在种群进化后期局部搜索效率较低，且很容易出现早熟收敛的情况[7]。遗传算法的另一个缺点是，算法的程序须通过二进制编码来实现，容易出现汉明悬崖问题，不利于优化算法的实际应用。但遗传算法具有独特的选择、交叉和变异操作，可以增加种群的多样性，提高寻优过程的可靠性。与遗传算法相比，粒子群算法不仅具有与遗传算法相同的优化能力，而且个体具有较好的记忆功能，适合求解复杂的优化问题，运行速度较快[8]。

本文中结合遗传算法和粒子群算法的优点，建立一种基于遗传粒子群优化的LQG控制算法，通过实值优化LQG控制器性能指标各权重系数。算法的基本思想是在粒子群优化算法基础上，增加遗传算法的选择、交叉和变异操作，实现种群的多样性，保证获得优化参数的全局最优解。具体流程如下：(1)给定优化算法参数，包括种群规模、迭代代数、选择概率、交叉概率、变异概率、惯性权重、加速因子等；(2)初始化种群，定义种群个体的速度vi和位置xi；(3)评价初始种群的适应度函数，对种群排序；(4)根据种群个体的历史最优位置和种群当前最优位置更新个体的速度和位置，生成新的种群；(5)对种群执行GA选择操作，根据适应度值排序的大小，以选择概率ps选择优良的个体，生成下一代；(6)对种群执行GA交叉操作，以交叉概率pc选择交叉的个体生成下一代；(7)对种群执行GA变异操作，根据变异概率pm在种群中选取一定数量的个体进行变异操作，生成下一代；(8)评价当前种群中的适应度函数，对种群排序；(9)如果满足迭代停止条件，得到全局最优解，否则转回步骤(4)，重复优化过程，直到满足迭代停止条件。

2.3 权重系数优化模型

优化方法是应用最优化原理，结合计算机技术确定某些参数或结构设计方案最优的工程设计方法。优化方法根据优化数学模型的特性，通过适当的优化算法求得最优解。优化数学模型主要包括设计变量和目标函数。针对2自由度1/4车辆悬架LQG控制器，权重系数优化的设计变量和目标函数如下。

2.3.1 优化变量

1/4车辆悬架LQG控制器中包含的权重系数有车身垂向加速度权重系数ρ1、轮胎动载荷权重系数ρ2、悬架动行程权重系数ρ3和悬架控制力权重系数ρ4。因此，优化过程的设计变量为

x=(ρ1,ρ2,ρ3,ρ4)T

(6)

2.3.2 目标函数

权重系数代表了性能指标在悬架控制中的重视程度，优化目标与悬架LQG控制目标相同，都是使车辆系统性能指标值尽量小。本文中将悬架控制得到的车辆系统性能指标值进行归一化，以无控制空气悬架的汽车性能指标值为基准，采用相同结构参数和相同激励下，有控制空气悬架汽车性能指标与无控制空气悬架汽车性能指标的比值作为优化目标函数，即

(7)

综合上述设计变量和目标函数，建立2自由度车辆悬架LQG控制器性能指标权重系数的优化数学模型为

(8)

3 控制策略仿真分析

控制仿真过程中所用模型参数和优化参数如表1所示。

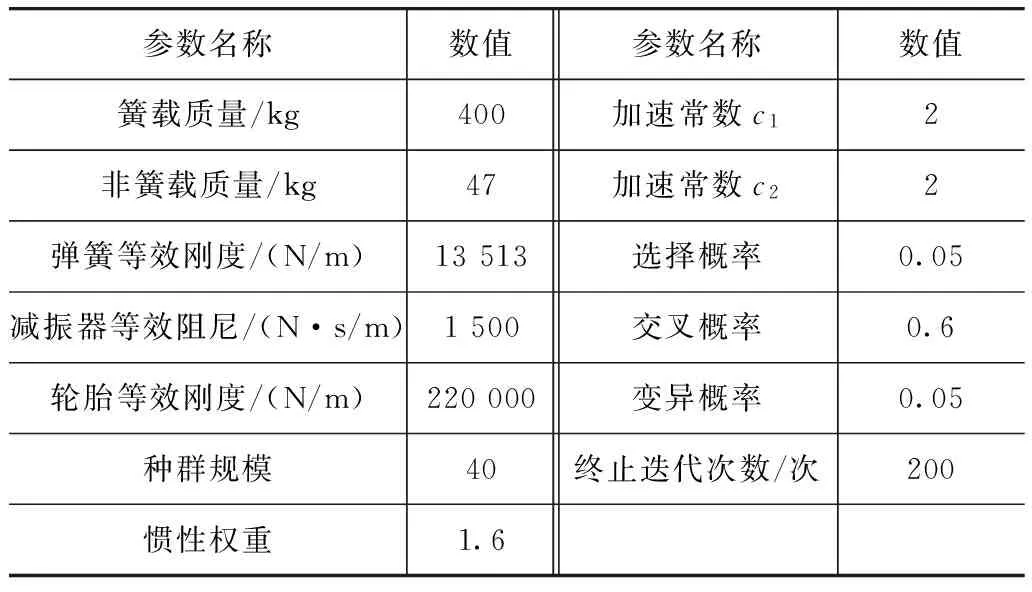
表1 仿真分析主要参数

设定优化设计变量取值范围分别为：ρ1∈[1 10]、ρ2∈[1 105]、ρ3∈[1 105]、ρ4∈[0 1]，最终通过遗传粒子群算法优化得到权重系数为ρ1=1.318 3，ρ2=4.12×104，ρ3=2.9×103，ρ4=2×10-5。根据轿车实际行驶情况，分别选取B级路面行驶速度70km/h和C级路面行驶速度40km/h作为仿真工况。在相同结构参数和路面激励下，分别对传统经验方法确定权重系数的LQG控制和遗传粒子群LQG控制进行了模型仿真。传统经验方法确定权重系数的LQG控制中，按照经验确定权重系数分别为ρ1=1，ρ2=10 000，ρ3=1 000，同时性能指标函数中不考虑悬架力的控制，即ρ4=0。两种控制方法仿真结果对比曲线如图3～图8所示。

从图3～图5的对比曲线可以看出，遗传粒子群LQG控制与LQG控制在相同结构参数和路面激励下得到的车身垂向加速度、悬架动行程和轮胎动载荷时域响应曲线在幅值和趋势上差异不明显。

从图6～图8的频域响应对比曲线中可知，两种控制方法的车身垂向加速度在低频和高频范围内几乎没有差别，在频率5～10Hz范围内，遗传粒子群LQG控制结果稍劣于LQG控制。比较轮胎动载荷的频域结果，遗传粒子群LQG控制在高频范围内控制效果明显优于LQG控制。车身垂向加速度和轮胎动载荷的对比结果表明，LQG控制虽然使车身垂向加速度幅值减小的更多，提高了舒适性，但轮胎动载荷明显恶化，破坏了操纵稳定性。与之相比，遗传粒子群LQG控制使两个指标的幅值和功率谱都有所减小，同时改善了平顺性和操纵稳定性。说明遗传粒子群LQG控制算法优于依靠经验确定权重系数的传统LQG控制算法，具有获得系统性能最优解的能力。另外，遗传粒子群LQG控制使悬架动行程也减小更多，有利于汽车平顺性的提高。

为了进一步验证遗传粒子群LQG控制方法，表2给出了两种行驶工况下，遗传粒子群LQG控制悬架和LQG控制悬架的车身垂向加速度、悬架动行程和轮胎动载荷性能指标仿真对比结果。从表中数据可以看出，在相同的结构参数和路面激励下，采用遗传粒子群LQG控制后，车身垂向加速度、轮胎动载荷和悬架动行程均方根都产生了下降，C级路面3个评价指标的变化率分别为-6.19%、-6.51%和-30.76%，B级路面的指标变化率分别为-16.33%、-6.44%和-31.93%。与之相比，经验确定权重系数的LQG控制悬架，在相同的结构参数和路面激励下，虽然车身垂向加速度均方根减小较多，但轮胎动载荷均方根反而增大，悬架动行程也稍有恶化。

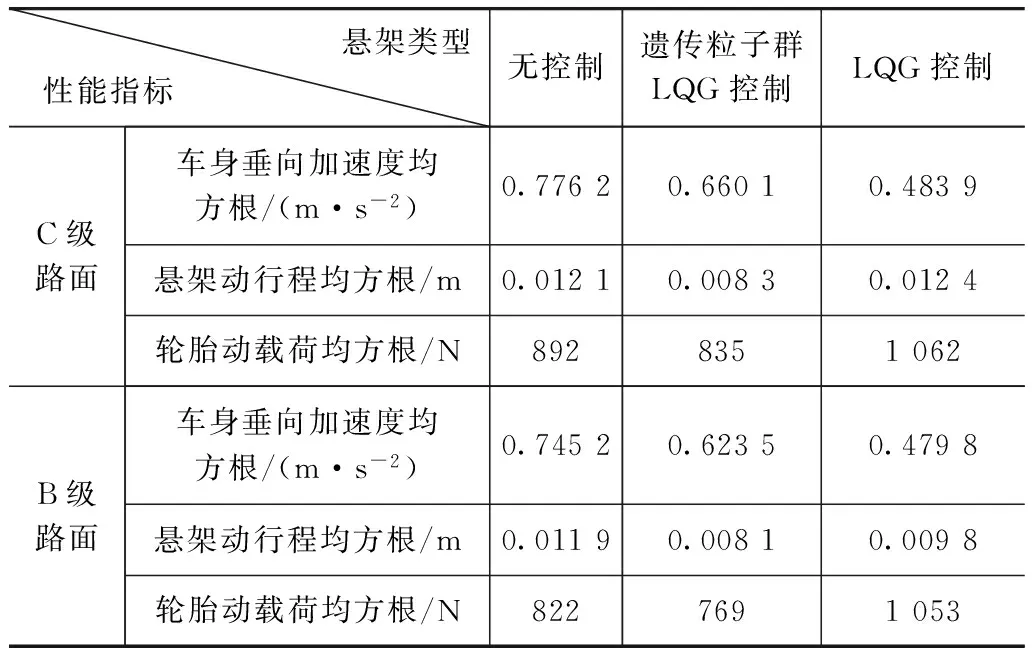
表2 随机输入路面仿真结果性能指标对比

4 结论

针对以往LQG控制权重系数选择方法的不足，在粒子群优化算法中增加遗传算法的选择、交叉和变异的操作，设计了车辆悬架的遗传粒子群的LQG控制方法，其中LQG算法用于实现悬架控制，遗传粒子群算法用于实现悬架控制器中性能指标权重系数的优化。通过单轮随机输入路面下1/4车辆悬架模型的控制仿真分析，对遗传粒子群LQG控制方法进行了验证。结果表明，所提出的遗传粒子群LQG控制方法能够同时改善汽车的平顺性和操纵稳定性，控制效果更接近最优解，为整车平顺性和操纵稳定性的遗传粒子群最优控制应用奠定了基础。

[1] Youn Ijoong.Optimal Control of Semi-active Automobile Suspension Including Preview Information[D].State University of New York at Stony Brook,1992.

[2] 兰波,喻凡.车辆主动悬架LQG控制器的设计与仿真分析[J].农业机械学报,2004,35(1):13-17.

[3] 黄卫忠,高国琴.基于遗传算法的最优控制加权阵的设计[J].计算机测量与控制,2003,11(10):761-762,772.

[4] 张国胜,方宗德,李爱民,等.基于遗传算法的主动悬架最优控制方法研究[J].中国机械工程,2007,18(12):1491-1495.

[5] 喻凡,林逸.汽车系统动力学[M].北京:机械工业出版社,2005.

[6] Nikzad S V, Naraghi M.Optimizing Vehicle Response in a Combined Ride and Handling Full Car Model by Optimal Control Strategies[C].SAE Paper 2001-01-1581.

[7] 周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.

[8] 崔航.基于微粒群算法的汽车行驶平顺性参数优化[D].长春:吉林大学,2007.

Genetic Particle Swarm LQG Control of Vehicle Active Suspension

Chen Shuang1& Zong Changfu2

1.CollegeofAutomotiveandTransportation,LiaoningUniversityofTechnology,Jinzhou121000；2.JilinUniversity,StateKeyLaboratoryofAutomotiveSimulationandControl,Changchun130022

Aiming at the deficiencies of traditional LQG optimal control-the experiences dependence in determining weighing factor, a genetic particle swarm LQG control algorithm is proposed by combining the updating of particle velocity and position in particle swarm algorithm with the selection, crossover, and mutation operation of genetic algorithm, to optimize the weighting coefficients of performance indicators.A 2-DOF 1/4 active suspension vehicle model is built and a simulation is conducted on vehicle suspension.The results of genetic particle swarm LQG control are compared with that of conventional LQG control and the outcomes indicate that the control algorithm proposed can concurrently improve both the ride comfort and handling stability of vehicle.

vehicle; active suspension; LQG control; genetic particle swarm algorithm

*辽宁工业大学教师科研启动基金(X201204)资助。

原稿收到日期为2012年12月26日，修改稿收到日期为2013年7月26日。