松弛方法在计算凝聚炸药爆轰问题中的应用*

陈秋阳，于 明

(1.中国工程物理研究院研究生部，北京 100088； 2.北京应用物理与计算数学研究所计算物理国家重点实验室，北京 100094)



松弛方法在计算凝聚炸药爆轰问题中的应用*

陈秋阳1，于 明2

(1.中国工程物理研究院研究生部，北京 100088； 2.北京应用物理与计算数学研究所计算物理国家重点实验室，北京 100094)

利用松弛近似，将非线性的凝聚炸药爆轰控制方程转化为线性的松弛方程组，并采用五阶WENO格式和五阶线性多步显隐格式对线性松弛方程组进行空间方向和时间方向的离散，由此建立具有高精度和高分辨率性质的计算凝聚炸药爆轰的松弛方法。建立的松弛方法可以避免求解Riemann问题及计算非线性通量的Jacobi矩阵，同时无需分裂处理反应源项。通过对凝聚炸药的平面一维定常爆轰波结构及球面一维聚心、散心爆轰起爆和传播过程的数值模拟，验证了所建立的松弛方法能够很好地计算凝聚炸药爆轰问题。

爆炸力学；松弛方法；高分辨格式；凝聚炸药；爆轰波

目前工程应用最广泛的计算凝聚炸药爆轰问题的数值方法是Lagrange方法[1]，它存在如下主要问题：(1)通常采用交错离散网格，总能量不守恒；(2)爆轰波在人为黏性捕捉过程中往往被抹平，且人为黏性系数靠经验确定；(3)时间和空间方向均仅有一阶精度，且难以推广到高阶精度；(4)使用细密离散网格时，网格容易扭曲从而导致计算失效。随着爆轰物理精密化要求，对爆轰细致流动图像与规律需要更深入地了解。高精度、高分辨率的Euler方法，由于能够较好地克服Lagrange方法的缺点，因此在计算凝聚炸药爆轰问题时得到越来越多的关注。国外应用的一些典型Euler方法有如下主要特点[2-5]：使用二阶Godunov型离散格式；采用简单形式状态方程和化学反应模型；运用反应率源项分裂格式等。

凝聚炸药爆轰的控制方程是带强刚性化学反应源项和复杂形式状态方程的非线性的双曲型守恒系统。强刚性化学反应源项和复杂形式状态方程这两个特点给运用高精度、高分辨率格式进行数值计算带来极大困难。

对强刚性源项的处理，不管是否采用分裂格式，都可能计算出错误的强间断传播速度。H.C.Yee等分析指出[6-7]，计算出错误的强间断传播速度来源于流动控制方程中对流项离散格式的数值耗散过大，从而引起虚假的化学反应。因此，正确捕捉爆轰波传播速度需采用数值耗散小的高分辨离散格式。目前，大多数高分辨离散格式都是基于完全气体等简单形式状态方程而采用Riemann求解器进行的。凝聚炸药爆轰过程中的未反应固体炸药和爆轰气体产物经常使用JWL形式、BKW形式、Davis形式、HOM形式等各种复杂形式状态方程，甚至使用SESAME数据库等形式，并且化学反应混合区通常在压力平衡和温度平衡的假设下进行温度迭代运算处理[8]，这样，采用基于Riemann求解器的高分辨格式来离散凝聚炸药爆轰控制方程是困难的。并且，为了更好地捕捉爆轰强间断，除了空间项的离散需要高分辨率，时间项的离散也需要高分辨率。从目前典型成果看[9]，无分裂的显隐格式是较好的处理方式：对流项离散采用高精度显式格式，刚性源项离散采用高精度隐式格式。

近年来正在发展的松弛方法是数值求解双曲型守恒系统的一种有力方法，其主要思想是利用松弛近似，将非线性的双曲型守恒系统转化为线性的双曲型松弛方程组，当松弛率趋近于零并满足一定的限制条件后，松弛方程组的解趋近于原守恒系统的解[10-13]。松弛方法的优点是可以直接采用一些简单、高效的高分辨率数值格式，勿需求解Riemann问题及计算非线性通量的Jacobi矩阵，因此它特别适合Riemann问题复杂或难以求解的双曲型守恒律方程。本文中将松弛方法应用于一维空间的凝聚炸药爆轰问题的数值计算。通过对凝聚炸药PBX9404的平面一维定常爆轰波结构及球面一维聚心、散心爆轰起爆和传播过程的数值模拟，验证所建立的松弛方法能够很好地计算凝聚炸药爆轰问题。

1 凝聚炸药爆轰控制方程

凝聚炸药爆轰在欧拉坐标下的一维化学反应流动方程为：

(1)

式中:

其中N为几何因子(N=0表示平面，N=1表示柱面，N=2表示球面)，R为化学反应率，本文中取三项式Ignition-Growth化学反应率[8]：

对凝聚炸药，化学反应率源项中包含有很大的数(如PBX9404炸药，I=7.43×1011、G1= 3.1、G2=400.0)，因此源项被认为是强刚性的。

本文中凝聚炸药爆轰的未反应固体炸药和爆轰气体产物采用JWL形式状态方程。在化学反应混合区采用压力平衡和温度平衡的假设下，混合区的状态可以表示(下标s表示固相、g表示气相)为：

式中:V=ρ0/ρ为相对体积，e为单位质量的内能，q为化学反应释放的单位热量。

2 松弛方程组的建立

利用松弛近似，将凝聚炸药爆轰控制方程式(1)转化为如下松弛方程组：

(2)

式中:w是中间变量，A=diag[a1,a2,a3,a4]是元素为正的对角矩阵，0<ε≤1是松弛率。

如此，将非线性的双曲型守恒系统(1)转化为线性的双曲型松弛方程组(2)，这样可以利用松弛方程组(2)的线性特征场构造简单、高效的高分辨率数值格式。文献[10-11]中分析指出，在满足-ak≤∂f(u)/∂u≤ak(k=1,2,3,4)条件下，如果松弛率ε→0，则式(2)的解趋于式(1)的解：w→f(u)。

下面简单分析松弛率在数值离散格式中的角色[12]。

由于w趋近于f(u)，可对w使用Chapman-Enskog级数展开，有：

(3)

将该展开式代入到式(2)中，保留ε的一阶项并消去w，可得：

(4)

从式(4)可以看出，引入松弛率相当于引入了数值耗散。

3 松弛方程组的离散求解

为方便求解，将式(2)进行对角化运算，有：

(5)

可以看出，方程组(5)具有常系数线性性质，其特征线为dr/dt=±A，特征线上的Riemann不变量为：w±Au。

考虑空间网格均匀的有限差分离散，式(5)的半离散表达式为：

(6)

方程组(6)进行时间离散时，可写成如下常微分方程组形式：

(7)

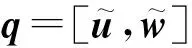
采用保持总变差有界(TVB)和单调性质的五阶精度线性多步显隐格式[9]来求解式(7)：

(8)

线性多步显隐格式的起步值采用三阶精度的显隐格式Runge-Kutta方法确定。

至此，获得凝聚炸药爆轰流动控制方程式(1)在空间和时间方向均具有五阶离散精度的数值格式。可以看出来，爆轰控制方程式在离散过程中没有进行Riemann问题求解。

4 典型算例分析

以凝聚炸药PBX9404为例，考察其平面一维定常爆轰波结构及球面一维聚心、散心爆轰起爆和传播性能。选取炸药尺度为4.0 cm，以CJ条件起爆。PBX9404炸药的未反应物JWL状态方程主要参数为(g-cm-μs制)：As=69.69、Bs=-1.727、R1s=7.8、R2s=3.9、ws=0.857 8、ρ0=1.842；爆轰气体产物JWL状态方程主要参数为：Ag=8.524、Bg=0.180 2、R1g=4.55、R2g=1.30、wg=0.38、q=0.102；相应的Ignition-Growth化学反应率参数可见文献[8]。PBX9404炸药的Von Neumann尖峰值为：pN=0.563，VN=0.607 5，uN=0.347；相应的CJ条件为：pCJ=0.370，VCJ=0.740 3，uCJ=0.229，DCJ=0.880 9。数值模拟时松弛率取为ε=10-7。

4.1 PBX9404炸药平面一维定常爆轰波结构

平面炸药左端起爆，计算获得爆轰达到定常状态时化学反应区内的压力p、速度v、相对比容V、反应道λ分布，如图1所示，所用离散网格为Δr=1/1 000、1/2 000、1/5 000、1/10 000 cm；同时获得爆轰CJ速度和压力Von Neumann尖峰值随网格大小变化关系，如图2所示。从计算结果看出，计算出的爆轰前导冲击波间断附近没有出现非物理振荡；随网格变小时数值解逐渐趋近精确解；PBX9404炸药反应区宽度约为0.01 cm(相应反应区内网格数目为10、20、50、100)，当采用Δr=1/5 000 cm或更小的离散网格尺度(即反应区内的网格数目至少达到50个)时，计算获得的数值解与精确解符合良好。图1中同时给出Δr=1/5 000 cm网格尺度下二阶MUSCL[13]格式的计算结果，可以看出本文的五阶精度格式结果更接近精确解。

数值模拟给出Δr=1/5 000 cm条件下炸药爆轰起爆过程几个典型时刻的压力和速度变化趋势，如图3所示，图中每条曲线对应的时刻为t=0.05、0.1、0.2、0.4、0.8、1.2、1.6、2.0、2.4、2.8、3.2、3.6、4.0 μs。可以看出，起爆约0.2 μs后爆轰基本达到定常状态。

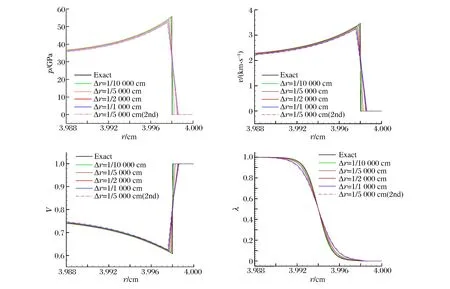
图1 PBX9404炸药化学反应区内物理量分布Fig.1 Distrubitions of physical variables in chemical reaction zone of PBX9404

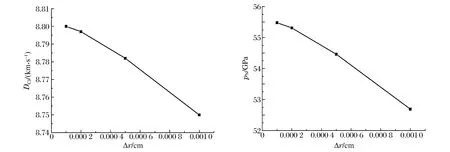
图2 PBX9404炸药CJ爆速和Von Neumann压力与离散网格尺度的关系Fig.2 Relations of the CJ velocity and Von Neumann pressure to the mesh sizes in PBX9404

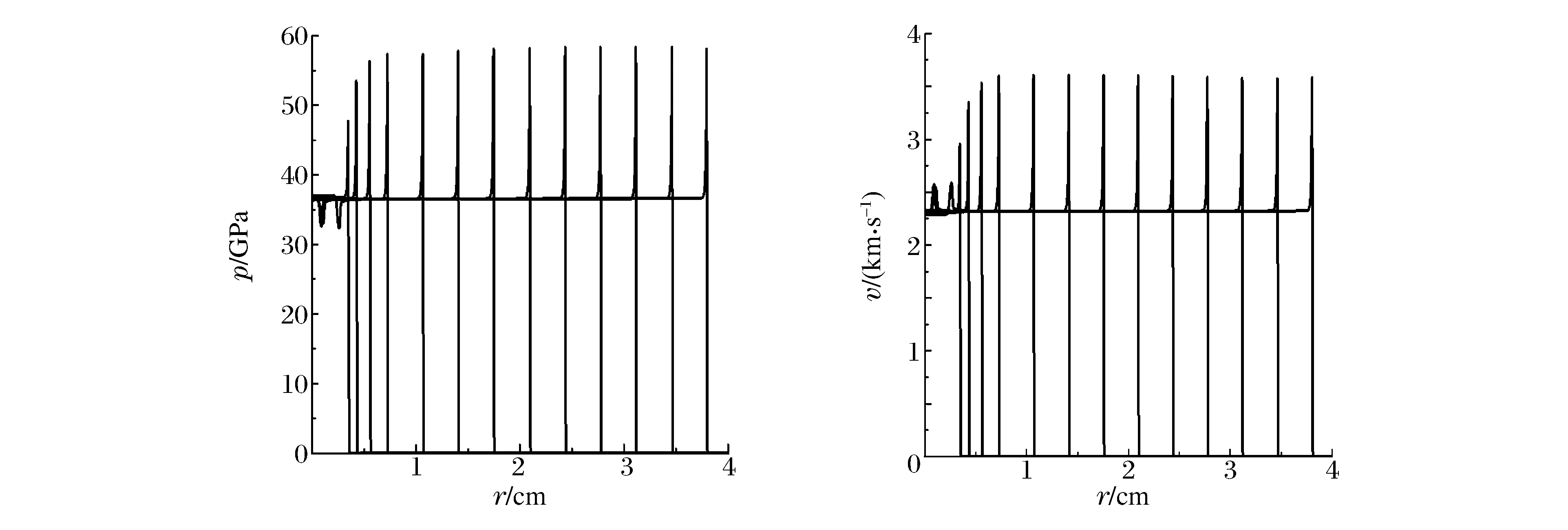
图3 PBX9404炸药平面爆轰波传播过程中压力和速度分布变化趋势Fig.3 Distributions of pressure and velocity of planar detonation wave in PBX9404

4.2 PBX9404炸药球面一维聚心爆轰的起爆和传播

炸药聚心爆轰波在传播过程中将逐渐出现超压爆轰现象，不正确的计算方法往往会获得反常的双波结构[1]。球状炸药外端起爆，计算获得炸药爆轰波传播过程几个典型时刻的压力和速度变化趋势，如图4所示，图中每条曲线对应的时刻为t=0.05、0.1、0.2、0.4、0.8、1.2、1.6、2.0、2.4、2.8、3.2、3.6、4.0 μs，所用离散网格为Δr=1/5 000 cm。可以看出，随着半径减小爆轰波压力和速度增大；爆轰波传播约0.8 μs后出现超压爆轰现象。

4.3 PBX9404炸药球面一维散心爆轰的起爆和传播

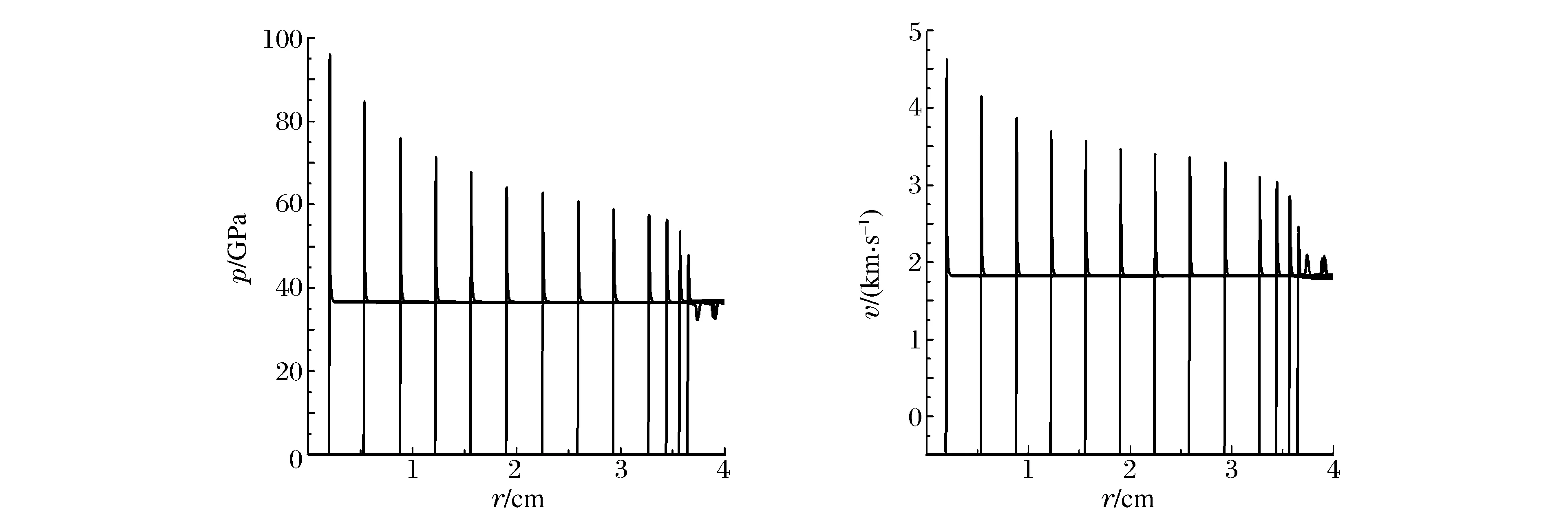
图4 PBX9404炸药球面聚心爆轰波传播过程中压力和速度分布变化趋势Fig.4 Distributions of pressure and velocity of spherically convergent detonation wave in PBX9404

炸药散心爆轰波在传播过程中前导冲击波阵面后面的物理量会急剧下降，差的计算方法不能正确处理发散几何因素的影响会导致爆轰波熄火[1]。球状炸药在中心区域起爆，计算获得炸药爆轰波传播过程几个典型时刻的压力和速度变化趋势，如图5所示，图中每条曲线对应的时刻为t=0.05、0.1、0.2、0.4、0.8、1.2、1.6、2.0、2.4、2.8、3.2、3.6、4.0 μs，所用离散网格为Δr=1/5 000 cm。从图中可以看出：炸药爆轰波的压力和速度均随波面半径的增加而增加；爆轰波传播2.8 μs后压力值变化不明显，散心爆轰的最大压力尖峰值约为0.551、最大速度尖峰值约为0.342，均低于相应的平面一维爆轰的压力和速度尖峰值。

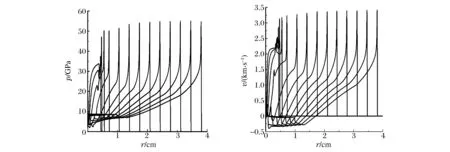
图5 PBX9404炸药球面散心爆轰波传播过程中压力和速度分布变化趋势Fig.5 Distributions of pressure and velocity of spherically divergent detonation wave in PBX9404

5 结 论

(1)将松弛方法应用于计算凝聚炸药的爆轰问题，采用五阶WENO格式和五阶线性多步显隐格式对爆轰松弛方程组进行空间离散和时间离散，避免了由于复杂状态方程引起的求解Riemann问题及计算非线性通量的Jacobi矩阵的困难。

(2)通过对PBX9404炸药的平面一维定常爆轰波结构及球面一维聚心、散心爆轰波传播过程的数值模拟，验证了所建立的松弛方法能够很好地计算凝聚炸药爆轰的主要特征，同时可以看出给出的离散格式具有高精度和高分辨率的性质。

(3)下一步的工作是将建立的松弛方法推广到二维空间下的凝聚炸药爆轰问题。

[1] Mader C L. Numerical modeling of explosives and propellants[M]. 2nd ed. New York: CRC Press, 1998.

[2] Henshaw W D, Schwedeman D W. An adaptive numerical scheme for high-speed reactive flow on overlapping grids[J]. Journal of Computational Physics, 2003,19(2):420-447.

[3] Kapila A K, Schwedeman D W, Bdzil J B. A study of detonation diffraction in the ignition-and-growth model[J]. Combustion Theory and Modeling, 2007(11):781-822.

[4] Banks J W, Schwedeman D W, Kapila A K. A study of detonation propagation and diffraction with compliant confinement[R]. UCRL-JRNL-233735, 2007.

[5] Schwedeman D W, Kapila A K, Henshaw W D. A study of detonation diffraction and failure for a model of compressible reactive flow[R]. UCRL-JRNL-M43735, 2010.

[6] Yee H C, Kotov D V, Sjogreen B. Numerical dissipation and wrong propagation speed of discontinuties for stiff source terms[C]∥Proceedings of ICCFD. Hawaii, 2011.

[7] Yee H C, Kotov D V, Shu C W. Spurious behavior of shock-capturing methods: Problems containing stiff source terms and discontuities[C]∥Proceedings of ICCFD7, 2012.

[8] 孙承纬,卫玉章，周之奎.应用爆轰物理[M].北京：国防工业出版社，2000.

[9] Hundsdorfer W, Ruuth S J. IMEX extensions of linear multistep methods with general monotonicity and boundedness properties[J]. Journal of Computational Physics, 2007(225): 2016-2042.

[10] Liu T P. Hyperbolic conservation laws with relaxation[J]. Communications in Mathematical Physics, 1987(108):153-175.

[11] Jin S, Xin Z. The relaxation schemes for systems of conservation laws in arbitrary space dimensions[J]. Communications of Pure and Applied Mathematics, 1995(48):235-276.

[12] Chalabi A. Convergence of relaxation schemes for hyperbolic conservation laws with stiff source[J]. Mathematics of Computation, 1999(68):955-970.

[13] Tang T. Convergence of MUSCL relaxing scheme to the relaxed scheme for conservation laws with stiff source terms[J]. Journal of Scientific Computing, 2000,15(2):173-195.

[14] Henrick A K, Aslam T D, Powers J M. Mapped weighted essentially non-oscillatory schemes: Achieving optimal order near critical points[J]. Journal of Computational Physics, 2005(207):542-567.

(责任编辑 曾月蓉)

Application of relaxation method for calculating detonation in condensed explosives

Chen Qiu-yang1, Yu Ming2

(1.GraduateSchool,ChineseAcademyofEngineeringPhysics,Beijing100088,China; 2.KeyLaboratoryforComputationalPhysics,InstituteofAppliedPhysicsandComputationalMathematics,Beijing100094,China)

Based on the theory of relaxation approximation, the nonlinear governing equations of detonation in condensed explosives are transformed into linear relaxation systems, which can easily adopt simple and effective high resolution scheme. A fifth-order WENO reconstruction scheme in spatial discretization and a fifth-order IMEX scheme of linear multistep methods with monotonicity and TVB in time discrtiezation are utilized, where it can leave out solving Riemann problem and computing the Jacobian matrix of the nonlinear flux, and make it unnecessary to split the stiff source term resulting from the chemical reaction. The developed method is applied to simulating the steady structure of one-dimensional planar detonation wave and unsteady initiation and propagation of one-dimensional spherically convergent and divergent detonation wave in condensed explosives PBX9404, with the results demonstrating the excellent performance of the present method.

mechanics of explosion; relaxation method; high resolution scheme; condensed explosives; detonation wave

10.11883/1001-1455(2015)06-0785-07

2014-05-07；

2014-10-07

国家自然科学基金项目(11272064); 中国工程物理研究院科学技术发展基金重点项目(2010B0201030)

陈秋阳(1990— )，男，硕士研究生;通讯作者： 于 明,yu_ming@iapcm.ac.cn。

O381 国标学科代码： 13035

A