南海北部典型区块岩石圈有效弹性厚度分析

张向宇

(1.国土资源部海底矿产资源重点实验室，广东 广州 510075;2.广州海洋地质调查局，广东 广州510075)

0 引言

板块构造理论的基础模型是刚性岩石圈在软流圈上漂浮并滑动，上覆在软流圈上的岩石圈对地质时间尺度(＞105a)的负载(包括地形、岩石圈内部负载、下部负载)所作出的响应，可以研究浮在流体层上的薄弹性板，这个薄弹性板的厚度即为岩石圈的有效弹性厚度(用Te表示)。

国内众多学者进行过关于岩石圈有效弹性厚度的研究，如袁炳强等(2001)通过对黑水—泉州地学断面Te值的计算，论述了用相关技术计算Te的方法及计算流程;赵俐红等(2004)在空间域采用垂直和水平受力的多个变刚度的三维有限差分方法来计算中国西部大陆岩石圈有效弹性厚度值;付永涛等(2005)以滇西为实例介绍了对相干值曲线计算的新认识和岩石圈Te研究的新趋势;安美建等(2006)利用地震波速反演得到的温度数据按照热学岩石圈标准研究了中国大陆岩石圈厚度。

本次研究选取南海北部4个典型区块，运用目前较常用的均衡响应函数法来求取每个区块的岩石圈有效弹性厚度值，根据计算结果初步分析研究区的构造运动情况。

1 均衡响应函数法原理

均衡响应函数法认为重力异常是由地形及其下部补偿密度引起，如果二者呈线性关系，则存在这样一个函数：当地形与之卷积时会重现所观测到的重力异常。这种函数称为均衡响应函数，相当于一个滤波器。

如果岩石圈的均衡响应是各向同性的，则布格重力异常对地形负载的响应是线性的，均衡响应函数可以由地形和布格重力异常的2位傅里叶变换获得(刘保华等，1998)，即：

一般情况下，N()与地形不相关，则更稳定的估计值为：

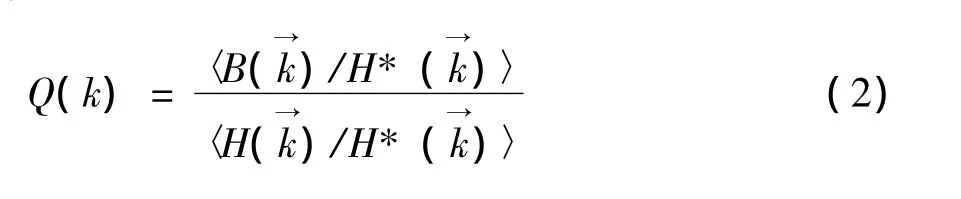
式(2)即为实验均衡响应函数的计算公式。*表示复数共轭;〈〉表示对不同波段或不同测线取平均值。

根据地球动力学理论，弹性板对地形负载的理论响应函数为(傅容珊等，2001)：

考虑海水层的负载影响，同时不考虑层间密度的不同，则得到：

式(4)中，ρc为地壳平均密度;ρm为地幔平均密度;ρw为海水平均密度;z为莫霍面深度;d为水深平均值;G为万有引力常数;g为重力加速度;D为弹性板刚度。有关系式：

有了实验及理论均衡响应函数公式，即可获得岩石圈有效弹性厚度值，将先期由其他手段获得的研究区平均水深值和平均莫霍面深度值代入公式(4)中并变换不同Te值，便可得到针对该研究区的一簇理论响应函数曲线;再将研究区实测水深数据和布格重力异常数据经过网格化，进行趋势消除后做离散傅里叶变换，由公式(2)求取实验均衡响应函数值;将实验均衡响应函数值与理论响应函数曲线进行最小二乘拟合对比可求取研究区有效弹性厚度值Te。

吴健生等(2011)对均衡响应函数法的可靠性和影响因素进行了模型计算分析，通过3个构造的典型地形模型，运用上述方法求取Te值，在合理的波数区间计算结果与模型初始Te值一致，证明该方法的可靠性。又通过另外3组模型分析了随机误差的加入和圆滑方式不同对计算结果的影响，与地形波长相近的误差的加入对方法影响较小，对于较复杂的地形情况，需要对实验均衡响应函数进行圆滑处理，采用中位数聚合圆滑处理效果较好。

2 典型区块Te值计算

选择的4个典型区块均位于南海北部，其位置分布如图1所示。

图1 研究区位置示意图Fig.1 Sketch showing location of the research area

4个区块的布格重力异常和地形数据已先期获得，首先将布格重力异常数据和地形数据进行同样精度的网格化，然后将重力和地形数据按测线取值后，分别进行离散傅里叶变换，代入公式(4)中求取实验均衡响应函数值，最后将多条测线的结果进行平均，得到该区块的实验均衡响应函数值。

求取理论均衡曲线时几个固定参数的取值为：

计算前4个区块的莫霍面深度已通过其他方法获得，故公式(2)中的d和z2个参数已知。这样就可以分别通过公式(2)、(4)计算出理论均衡曲线和实验均衡响应函数，并进行曲线拟合。

首先计算区块1的实验均衡响应函数，选取该区块实测水深数据和布格重力异常数据，经相应处理后运用公式(4)得到的结果如图2所示。

图2 区块1实验均衡响应函数计算结果区块Fig.2 Calculation by experimental isostatic response function for the block

从图2中看到，通过谱相关方法得到的实验均衡响应函数较离散，且因为地下结构复杂，如岩石圈之上还附着沉积盖层，导致散点中还包含了来自地下不同地层的响应，为分离出来自岩石圈的响应函数散点，引入统计学中常用的聚类分析方法对散点进行分类，聚类结果如图3所示，图中每一种颜色代表1组分类。

图3 区块1实验均衡响应函数聚类分析结果示意图Fig.3 Schematic diagram showing cluster analysis result by experimental isostatic response function for the block 1

图3中第①—⑥组的散点对应的均衡响应函数值都较小，根据谱分析可知这些散点并非是来自地下岩石圈部分的响应，而是其他部分(如沉积盖层)的响应，故进一步处理前应删除这部分点。

在通过聚类分析删除掉部分散点后，需要运用圆滑手段对数据进行处理，这里采用滑动窗口中位数圆滑方法，得到的最终结果见图4。

图4 区块1均衡响应函数法处理后结果Fig.4 Results after processing by the isostatic responsefunction method for the block 1

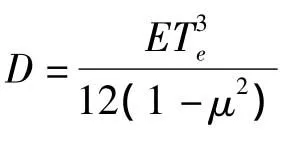
同样，对于其他3个区块也用此方法进行计算，为了进行对比，将4个区块的结果同时呈现在1张图中，取d=3 000 m，z=26 km(依据4个区块水深和莫霍面深度数据给出)作理论均衡响应函数曲线(图5)。

图5 4个区块均衡响应函数法计算结果对比图Fig.5 Comparison of the results determined by isostatic response function for the 4 blocks

图5显示，在0.01～0.04 km－1波数区间内，4个区块拟合的岩石圈有效弹性厚度值相近，其中区块1的厚度值最小，约为55 km;区块3的厚度值较区块2略大，区块2的厚度值约为65 km，区块3的厚度值约为70 km;区块4的厚度值最大，约为80 km。根据图1所示4个区块的相对位置可知，对于南海北部陆坡区，岩石圈有效弹性厚度由西北向东南方向逐渐增大。在0.04 km－1波数处，4个区块的实验均衡响应函数均出现了拐点，在0.04～0.08 km－1波数区间内，4个区块的实验均衡响应函数均集中在D=1.0×1023N·m理论曲线附近;而在0.08 km－1波数处，4个区块实验均衡响应函数均出现了第二个拐点;在大于0.08 km－1波数区间内，实验均衡响应曲线逐渐减小。由此分析，该研究区发生了多次构造运动，出现了不同时期地形的叠加现象，因此实验均衡响应函数出现了2个拐点。根据有关文献分析，在0.01～0.04 km－1波数区间内拟合得到的厚度值为现今时期的岩石圈有效弹性厚度值，可以用来分析地质构造，而其他波数区间内的拟合厚度值可以为分析早期岩石圈地质构造运动提供依据。

3 结论

(1)运用均衡响应函数法推算出了南海北部区域4个典型区块的岩石圈有效弹性厚度值，由对比可知，在南海北部陆坡区，岩石圈有效弹性厚度值由西北向东南方向逐渐增大。

(2)通过实验均衡响应函数的变化，可以看出研究区经历了多期构造，如今的地下结构为多期构造运动叠加造成。

安美建，石耀霖.2006.中国大陆岩石圈厚度分布研究［J］.地学前缘，3(3)：23－30.

傅容珊，黄建华.2001.地球动力学［M］.北京：高等教育出版社.

付永涛，范守志，施小斌.2005.关于岩石圈有效弹性厚度的地质理解［J］.地质科学，40(4)：585－593.

刘保华，吴金龙，辛柏森，等.1998.冲绳海槽海底地形的补偿模式研究I：理论均衡响应函数的计算［J］.海洋学报，20(6)：70－75.

时立文.2012.SPSS 19.0统计分析［M］.北京：清华大学出版社.

吴健生，张向宇.2011.均衡响应函数法影响因素的模型分析［J］.同济大学学报：自然科学版，39(11)：1703－1709.

袁炳强，王平.2001.用相关技术计算大陆岩石圈有效弹性厚度［J］.西安工程学院学报，24(2)：55－58.

姚伯初，万玲.2006.中国南海海域岩石圈三维结构及演化［M］.北京：地质出版社.

赵俐红，姜效典，金煜，等.2004.中国西部大陆岩石圈的有效弹性厚度研究［J］.地球科学：中国地质大学学报，29(2)：481－488.