卷积公式在求连续型随机变量和分布中的应用

王 静，赵会娟

(河北科技师范学院数学与信息科技学院，河北 秦皇岛，066004)



卷积公式在求连续型随机变量和分布中的应用

王 静，赵会娟

(河北科技师范学院数学与信息科技学院，河北 秦皇岛，066004)

对卷积公式进行推广，得到了求二维连续型随机变量线性组合分布的卷积公式，该方法在求二维连续型随机变量线性组合分布时较分布函数法更加简洁、高效，更适用于此类问题的求解。

连续型随机变量；分布函数；卷积公式

对二维连续型的随机变量(X,Y)，总可以用分布函数法求得函数Z=g(X,Y)的密度函数。但这种方法计算量大，尤其当(X,Y)的密度函数p(x,y)是分段函数时，计算过程较为繁琐。当Z=X+Y时，文献[1]中介绍了卷积公式法，这种方法可以看作是特殊情形下分布函数法的简化。特别的，当Z=X+Y是分段函数时，用卷积公式求随机变量Z的密度函数pZ(z)时，如何分区间讨论及确定积分限是一个难点。笔者致力于对卷积公式及其应用进行尽可能详细地分析，为读者今后学习、使用卷积公式提供一定帮助。

1 卷积公式的推广

本次研究中提到的随机变量均指连续型的随机变量。

定理1[1]设二维随机变量(X,Y)的概率密度函数为p(x,y)，X,Y的边沿概率密度函数分别为pX(x),pY(y)，Z=X+Y，则Z的概率密度函数为

(1)

或

(2)

当X与Y相互独立时，则

(3)

或

(4)

公式(3)与(4)称为卷积公式。

采用公式(1)、公式(2)，或公式(3)、公式(4)，求出Z=X+Y的密度pZ(z)的方法称为卷积公式法。

卷积公式法可用来求X与Y和的密度，如果函数是X与Y的线性组合，即Z=aX+bY,(a,b≠0)，用卷积公式法还可以求Z的密度。由此引出下面的定理2。

定理2 设二维随机变量(X,Y)的概率密度函数为p(x,y),X,Y的边沿概率密度函数分别为pX(x),pY(y),Z=aX+bY,(a,b≠0)，则Z的概率密度函数为

(5)

或

(6)

当X与Y相互独立时，则

(7)

或

(8)

公式(7)与公式(8)称为X与Y的卷积公式。

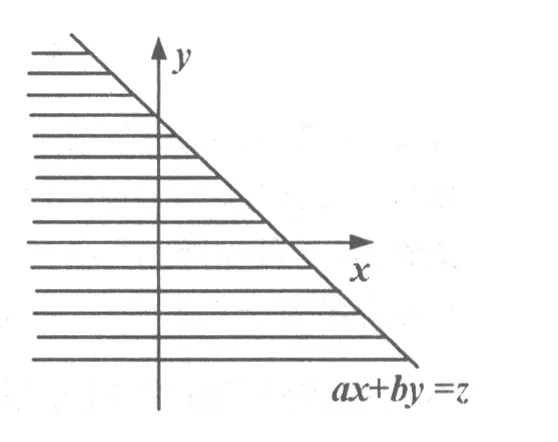
图1

证明 据y前系数b的正负，积分区域D位于直线ax+by=z的下方或上方。下面分情况讨论。

若b>0，分2种情况讨论如下：

两边对z求导，得到：

类似的，可以得到

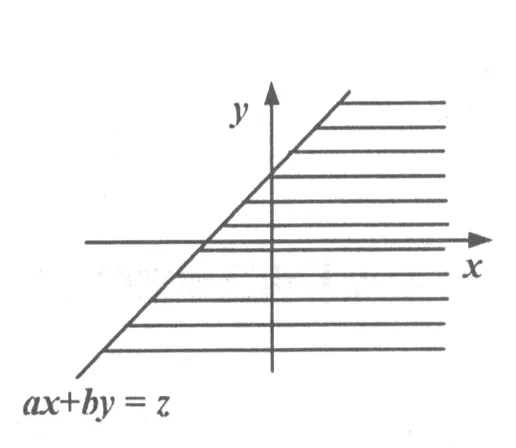
图2

b<0时，和上面讨论相似，故略。

同样地，采用公式(5)、公式(6)，或公式(7)、公式(8)，求出Z=aX+bY,(a,b≠0)的密度pZ(z)的方法就成为卷积公式法。

2 分布函数法与卷积公式法的应用与比较

例1 设随机变量X,Y相互独立，并分别在[-5,1]与[1,5]内服从均匀分布，其概率密度函数分别为

求随机变量Z=X+Y的分布密度函数。

解法1 分布函数法。

首先，随机变量X,Y相互独立，故得X,Y的联合密度函数

当z<-4时，FZ(z)=0；

当z≥6时，FZ(z)=1。

解法2 卷积公式法。

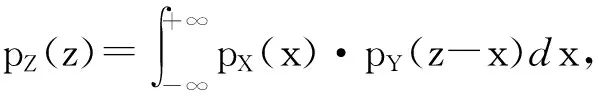
当z在[-4,6]的不同区间段上取值时，自变量x的变化范围不同，分段如下：

当z<-4或z≥6时，PZ(z)=0;

故

例2 设随机变量(X,Y)的概率密度函数为

解法1 分布函数法。

设Z的分布函数为FZ(z)，则

根据(X,Y)的密度函数p(x,y)的实际取值范围，对z的范围讨论如下：

当z≤0时，FZ(z)=0；

故得Z的密度函数

解法2 卷积公式法。

当z≤0时，pz(z)=0；

故Z的密度函数

3 结 论

通过以上两道例题，可清楚地看到卷积公式法在求二维随机变量(X,Y)的线性组合函数Z=aX+bY,(a,b≠0)的密度时的简捷应用。在求Z=aX+bY,(a,b≠0)的密度函数时，使用卷积公式法较分布函数法有两点优势：其一，z的分段区间易讨论，根据x,y的实际取值范围就可确定；其二，计算简便，在z的实际取值区间内，pZ(z)是一个定积分容易计算，而在分布函数法中，相应区间的FZ(z)是一个二重积分，计算起来较麻烦。

[1] 郑国萍，郭亚君.概率论与数理统计[M].北京：中国农业科学技术出版社,2010.

[2] 盛骤，谢式千，潘承毅.概率论与数理统计[M].第三版.北京：高等教育出版社，2001.

[3] 孙清华，孙昊.概率论与数理统计内容、方法与技巧[M].第二版.武汉：华中科技大学出版社，2006.

[4] 霍海峰，温鲜.二维连续型随机变量卷积公式探讨[J].价值工程，2011(27):305.

[5] 赵娟，张晓阳.卷积公式的推广及应用[J].淮北师范大学学报:自然科学版，2012，33(1)：86-89.

[6] 罗建华.卷积公式的应用注记[J].中南林业科技大学学报:自然科学版，2007,27(1):152-154.

[7] 胡杨利，李应求，赵晓芹.卷积公式的妙用[J].当代教育理论与实践，2013,5(12):185-186.

[8] 刘怡娣.卷积公式商分布的推导与应用[J].长春教育学院学报，2013，29(3):98-99.

(责任编辑：朱宝昌)

The Application of Convolution Formula in Two Dimension Continuous Random Variable’s Sum Distribution

WANG Jing，ZHAO Hui-juan

(School of Mathematics and Information Science & Technology, Hebei Normal University of Science & Technology, Qinhuangdao Hebei，066004,China)

The convolution formula was generalized in the paper, and general convolution formula which to solve two dimension continuous random variable’s linear combination distribution was obtained. Comparing with distribution function, the new formula is more succinctly and more efficient, which will be better for solving such problems.

continuous random variable; distribution function; convolution formula

10.3969/J.ISSN.1672-7983.2015.02.012

2015-01-31; 修改稿收到日期: 2015-06-01

O211.5

A

1672-7983(2015)02-0057-04

王静(1981-)，女，硕士，讲师。主要研究方向：代数密码。