量子力学中基于离散化空间的的一维定态问题的快捷数值试验
黎永耀,刘 丹,吕红英,刘 岩
(华南农业大学 电子工程学院 应用物理系,广东 广州 510642)
利用计算机对物理问题进行数值或仿真研究是近年来物理研究的一种非常重要的理论研究手段.在传统的量子力学教学中,适当引入数值仿真的模块,近年来受到不少教学工作者的关注[1,2],也是理论物理教学改革一个方向之一[3].通过在教学中引入一些简单的数值方法,通过编程,计算机做图获得量子力学的结果并和解析结果做对比,不仅对于学生理解量子力学的基本概念和思想有重要的促进作用,可以提高学生的学习兴趣,而且可以为其今后进一步深造进行科学研究打下一定的基础.
本论文对量子力学中一维定态问题中求解谐振子能量本征值和波函数的问题展开讨论,并借助空间离散化的方案,构造坐标表象的矩阵方程,通过矩阵对角化的方法获得系统的本征值和本征波函数.其中矩阵的对角化过程通过数学软件MATLAB实现,对比与传统的量子力学教学,该方法简单快捷有助于学生理解一维问题的物理含义和本质,同时对表象理论,和矩阵力学的学习和理解有较大的帮助.
传统的量子力学教科书中,对于谐振子能量本征值的求法大多都是利用特殊函数的方法,通过引入厄米多项式,获得谐振子波函数和能量本征值的解析表达式.由于现代的教学系统中,学生在数学物理方法等重要课程的课时数收到很大的限制,特殊函数并不是作为一个主要讲授内容出现在数学物理方法中,因此,许多学生在学习这一部分的时候,并没有掌握太多的特殊函数只是,这对学生理解和掌握这部分内容带来极大的困惑.本论文将提出一种简单的基于坐标表象的数值差分方法,把坐标表象下的连续哈密顿量变成一个矩阵形式,通过对角化获得能量本征值和本征函数.这些简单的方法可以辅助同学们理解和学习波函数和能量本征值的本质意义,并加深他们对求解手段的熟悉,对于他们理解解析的方法有重要的帮助.
在自然单位制(m=攸=ω=1)下一维谐振子定态薛定谔方程为如下的形式:
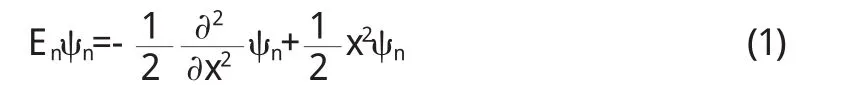
其结果为
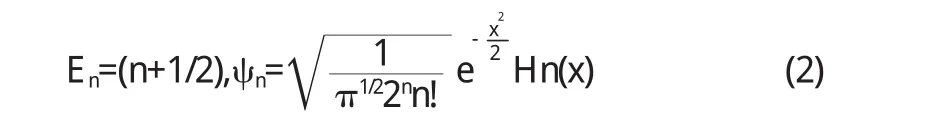
其中Hn(x)为厄米多项式[4].
众所周知,数值方法的一个核心问题是把连续的问题离散化,我们把空间离散化为x1,x2,…xN,相应的波函数在这些离散坐标点下表示为一个列矩阵:(其中上标“T”代表一个转置的操作),对于该一维问题我们采用最常规的离散方案,把方程(1)中两个对时间和空间的一阶和二阶导数改写成如下的形式[5]


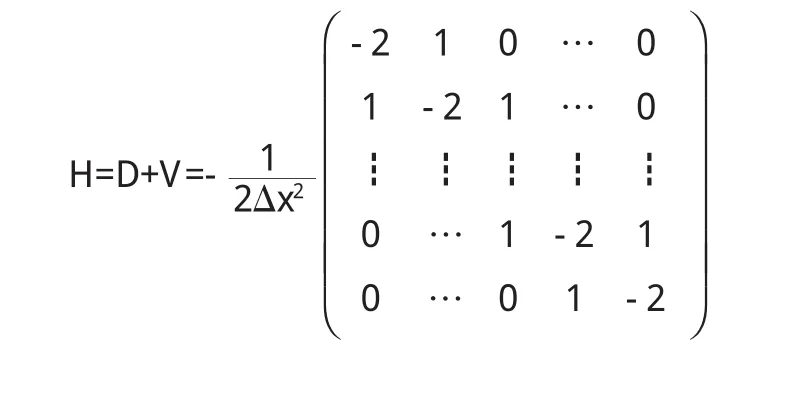
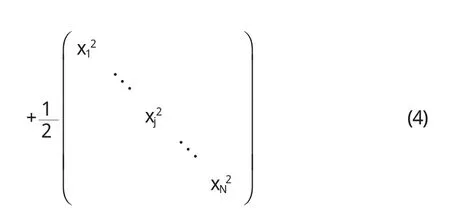
其中N为离散化后空间的网格数.相应的定态薛定谔方程(1)变成如下的矩阵形式

根据量子力学中矩阵力学的知识,我们知道,在Q表象下,力学量算符可以用一个矩阵来表示,如果Q为该力学量的本身,则该矩阵为一个对角矩阵,对角元为力学量的本征值.如果Q不是该力学量,则可以通过幺正变换把矩阵进行对角化来获得本征值,而幺正矩阵的相应本征值的列矩阵为该本征值在Q表象下的本征矢[6].
基于上述的分析,我们把方程(4)中的矩阵进行对角化.矩阵对角化是一种很成熟的算法,在这里我们是基于一个常规的商用软件MATLAB对其进行对角化,在MATLAB平台下,我们输入

就可以把哈密顿矩阵对角化[7].在命令(6)中,V和E均为一个N×N的方阵,其中,E为对角矩阵,第j个对角元即为能量本征值Ej,而V则为幺正矩阵,其第j列的子矩阵,为Ej的本征矢,即为离散形式下的坐标波函数.注意,通常来说,这个通过MATLAB获得的离散形式的波函数是没有被归一化的,所以,需要运用归一化条件对其进行归一化.
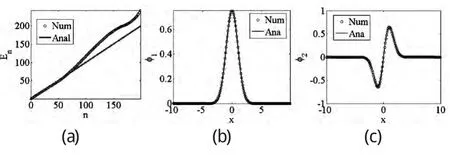
图1(a)解析结果(红色线)与数值结果蓝色圆圈的对比.我们选择的范围为x∈[-10,10],离散化为200个格点.从图中我们可以看到在低能态的时候(n<70)蓝色圆圈和红色线完全符合,但是在高能态之后,蓝色圆圈偏离与红色线.(b)基态波函数的解析表达式(蓝色线)和归一化后的V矩阵的第一列数值结果比较,两者完全符合.(c)第一激发态的波函数解析表达式和归一化后的V矩阵的第二列数值结果的比较,两者完全符合.
图1为数值结果和解析结果的对比,从图1(a)中我们可以看到,当体系处于低能态的时候,数值结果和解析的结果稳合得很好,但是当趋向于高能态的时候,数值结果和解析结果就出现了偏离,这个偏离是我们在数值上不得不使用有限的空间及离散格距所造成的,我们可以通过增加我们数值窗口的宽度和使用更多的各点数使得这个解析结果和数值结果稳合的距离增长.不过其代价就是需要更多的计算机资源去计算矩阵对角化了.图1的结果表明,我们采用x∈[-10,10]的数值空间,和200个格点数,已经可以很好得在n<70这个范围内把一维谐振子的能量本征值和本征函数准确表达出来.
通过上述的例子,我们通过引入差分和空间离散化,简单快捷地把谐振子的能量本征值和本征函数计算出来.该方法不仅可以使得学生更方便地去理解谐振子模型的物理性质,更使得学生对于表象理论,矩阵力学和幺正变换的含义有更深刻的认识.并可以为学生将来进一步科研进修,做数值仿真打下良好的基础.值得一提的是,量子力学问题中,可解析求解的系统并不多,该方法对于处理各种处于束缚形式的一维势阱问题具有很大的实用价值.
〔1〕黎永耀,麦志杰,吴剑雄,付神贺,刘岩.基于 Matlab 平台下量子力学课中的“实验”课[J].赤峰学院学报,2011,27(10):13-14.
〔2〕陈桂华,谭穗妍,庞玮.光学课程中一个数值仿真例子:光折变离散孤子[J].赤峰学院学报,2012,28(9):10-12.
〔3〕刘岩,杨小红,罗志环,黎永耀,林建荣.高校《理论物理导论》课程教学改革的探索与实践[J].赤峰学院学报,2009(25):18-19.
〔4〕曾谨言.量子力学(第三版)(上,下册)[M].北京:科学出版社,2001.
〔5〕陆金甫,顾丽珍,陈景良.偏微分方程差分方法[M].北京:高等教育出版社,1988.
〔6〕S.福里格.实用量子力学(上册)[M].北京:高等教育出版社,1983.
〔7〕张志涌,杨祖樱.Matlab教程[M].北京航天航空大学出版社,2006.

