运用建模思想 解决数学问题

江苏盐城市第二小学（224005） 商林付

解决问题的教学一般要经过阅读、观察、分析、操作、抽象等几个过程。解决问题的方法有许多，但是自从新课标实施以来，关注数学建模，学会用建模思想指导教学，解决数学问题则是其极力提倡的。那么，怎样才能有效运用建模思想，帮助学生解决数学问题呢？

一、理解四则运算意义，构建解决问题的基本模型

四则运算是解决问题最基本的模型，这是因为所有的解决问题都是与加减乘除分不开的，更是在理解运算意义的基础上进行的。因此，在教学中，教师可在四则运算意义的基础上引导学生建立基本的数学模型，进而达到解决问题的目的。

例如，在解决“桌上有3个盒子，每个盒子里有5个乒乓球，一共有几个乒乓球”这个问题的过程中，教师可以结合具体情境引入“5＋5＋5”这个加法算式合并的例子，然后在此基础上抽象出“份数乘个数”这个数学模型，帮助学生轻松解决数学问题。

这样教学，集解决问题与理解算法于一体，不仅有助于学生认识四则运算在解决问题中的价值，而且还有效地增强了学生的应用意识。

二、探析信息的关联性，构建解决问题的关系模型

在新课改理念指引下，现行的数学教材较以往有了很大改变，那就是弱化了“数量关系”这个环节，直接从“情境创设”跳转到了“实际应用”，这对我们的教学提出了挑战。因此，教师要善于从具体的情境中抽象出数量关系模型，以使学生在直观理解的基础上把握问题之间的具体联系，并使之在建模过程中得到内化与发展，提高学习效果。

例如，在学习“购物问题”时，以下表为例，笔者是这样引导学生构建关系模型的：

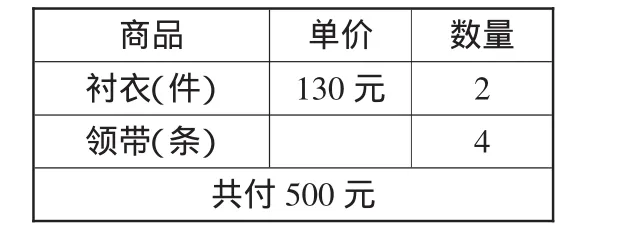
商品 单价 数量衬衣（件） 130元 2领带（条） 4共付500元

1．从图中你看到了哪些有价值的数学信息？利用这些信息可以帮助我们解决什么问题？

2．从给出的已知条件“衬衣单价130元，数量2件”中，你能求出什么？（引导学生抽象出模型：单价×数量＝总价。）

3．题目中有哪些未知条件？应该如何解决？（引导学生得出模型：单价＝总价÷数量。）

4．在领带总价不知的情况下，铺路搭桥，从中间条件出发解决问题，得出方法模型：领带总价＝500元－衬衣总价。

5．自行尝试列式计算。

在这个教学过程中，教师主要从问题之间的相互关联性入手，引导学生进行层层剥茧式的探究学习。在这个学习过程中，学生边探析边构建关系模型，轻松地解决了数学问题。

三、引导分析与综合，构建解决问题的思维模型

分析与综合是数学学习最基本、最重要的思维方法。在数学教学中，教师应注重引导学生进行分析与综合，构建解决问题的思维模型，进而促进学生有效解决问题。

例如，在解决“小英家养了12只白兔，7只黑兔，求白兔比黑兔多几只”这个问题的过程中，教师可以引导学生轻声读题，学生在一遍又一遍的朗读中得出已知条件以及具体要求的问题是什么，必要时可以通过画图的方式来帮助学生分析。

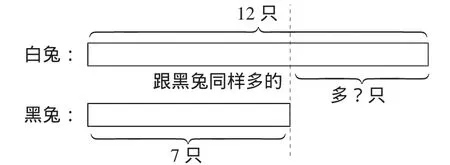
在结合图例分析的过程中，教师要引导学生说出要求的是哪一部分，以及虚线在图中表示的意义等，在此基础上，经过分析与综合得出“求比一个数多几”的问题的思维方式，从而帮助学生构建出“要求出谁比谁多几，就要从多的数中减去和它同样多的部分，用减法计算”的思维模型。

由此可见，巧用分析与综合，不仅可以帮助学生理清解题思路，找到解决问题的突破口，而且还可以逐步提升学生运用所学知识解决实际问题的能力。

总之，在数学学习过程中，运用模型思想可以有效降低学生的学习难度，使学生在基本数学模型的指引下，思考问题方便直接，解决问题有凭有据。因此，教师要注重建模思想在解决问题中的渗透，逐步提高学生解决问题的能力。