人的高度,就是数学教学的高度
江苏启东市中小学教师研修中心(226200) 蔡宏圣(特级教师)
一、学科教学的终极使命
近年,北京师范大学有关人员做了一个专题研究:以联合国系统专门人才为对象,收集了1742份招聘说明书,并对国际公务员进行了深入访谈,提炼了国际组织人才需要具备的十大基本素养。研究结果表明,“崇尚专业”是联合国秉持的重要原则,除此以外,国际组织人才还需要:
民族文化身份认同:即爱自己的祖国,爱国才更为自信和积极;
尊重多元文化的价值观:尊重不同的文化,自觉审视自身的偏见;
语言沟通能力:起码掌握两种联合国官方语言,并能清晰简练和准确可信地沟通、演讲、协商。
团队合作能力:能与各种身份的人合作,能灵活地转换合作中的角色;
学习意愿和持续学习的能力:能根据任务需要及时分享知识、更新知识;
……
进一步思考,我们的教学活动中是否有和上述基本素养一一对应的专一课程?国际组织人才需要具有认真负责、积极抗压的个性,那我们是否应该设计一个课程直接来培养学生这样的个性?事实上,与上述基本素养相对应的专一课程是不存在的,显然,学科教学的最终使命不在于学科本身,而在于通过学科学习的独特价值、独到路径去培养人。这也正是北京十一学校李希贵先生所说的:“我们学校的教师不是教学科的,而是教学生的。”“不是教学科的”,不是对学科的漠视,更不是对学科的否定,而是在把握学科本质基础上对学科的超越,站在人的高度上去育人!
二、数学学习的终极价值
一个普通人,通过义务教育起码要学九年数学,但步入社会却又很少用数学,于是,很多人问:为什么人人都要学数学?数学学习的终极价值何在?
为此,日本数学教育家米山国藏在《数学的精神思想和方法》中指出,学生走出校门后很快就忘掉学校里所学的数学知识,“然而不管他们从事什么工作,唯有深深地铭记在头脑中的数学的精神、数学的思想、研究的方法和着眼点等这些都随时随地发生作用,使人受益终身。”美国数学家M·克莱因在他的名著《西方文化中的数学》中指出:“数学是一种精神,一种理性的精神。正是这种精神,激发、促进、鼓舞并驱使人类的思维得以运用到最完善的程度,也正是这种精神,试图决定性地影响人类的物质、道德和社会生活;试图回答人类自身存在提出的问题;努力去理解和控制自然;尽力去探求和确立已经获得知识的最深刻和最完美的内涵。”很显然,我们需要在知识技能的学习过程中引导学生积淀数学的精神,唯有数学的精神才能融入一个人的血液、个性、举止投足间,成为其一生都能带在身边的财富。
更为具体地说,在小学数学教学活动中,宜结合相关知识的学习与相关技能的训练,利用数学的内在魅力帮助学生拥有下面这些素养。
理性的态度。“一张白纸不停地对折会有多高”,这样的活动不在于计算出最终结果,而在于形成这样的态度:遇到问题,不要凭空猜测,也不要迷信权威,自己动手尝试做做,收集数据,用理性的方式作出回答。学习数学,就是要学会如何独立地,运用逻辑性的思维解决问题。
思考的方法。数学是思维的体操。学习数学,就是学习如何思考——如何把事物分成几类,如何比较不同事物间的异同,如何有条理地进行推理,如何在大量例子的基础上提炼出规律来,如何在已有知识的基础上提出新的猜测,如何对猜测进行验证,等等。
开放的心态。无论是多么聪慧的人,终究有思维的盲区。所以,数学学习首要的是独立思考,然后是自信大方、简明扼要地表达,以及从容淡定、有根有据地争辩。不要顾忌对和错,任何想法都值得骄傲和分享;也不要坚持己见,谁更有道理就接受谁的想法,而且一个人有一个想法,通过交流,就能对知识就有更多的感悟,在这样的学习过程中,学生不但能得到提高,还会养成坦诚开放的心态和交流辩论的技巧。
反思的习惯。古人说“千金难买回头看”,华罗庚也说:“做了好题不回顾反思,就像入了宝山,却空手而归。”真正的智慧都不是别人告诉你的,而是自己醒悟的。所以,探索了知识、解答了某题,对于个人来说不仅获得了知识,更大的价值在于作为第三者对自己刚才所思所为的回顾总结,想想是什么保证了解答的正确,是什么导致了探索的曲折。这些才是人生的一笔财富。
坚韧的品质。学习没有坦途。课堂里学习的任何一个数学结论,都是几十年乃至几百几千年人类思维的结晶。要在教学中捕捉契机,让学生体会,在学习中遇到困难的时候,只有坚持下去才能获得成功。不以个人的聪慧论英雄,而以能不能坚持论成败。
三、数学育人的终极入口
理论上,一切教学都具有教育性,但如果不是恰当的方式,即便教师有良好的教育愿景,也可能事与愿违。因此,学科教学的育人功能,一方面要深究整个课程体系中每个学科不可替代的独到育人价值,另一方面也要寻找最能体现学科特点的、贴切的学科路径。
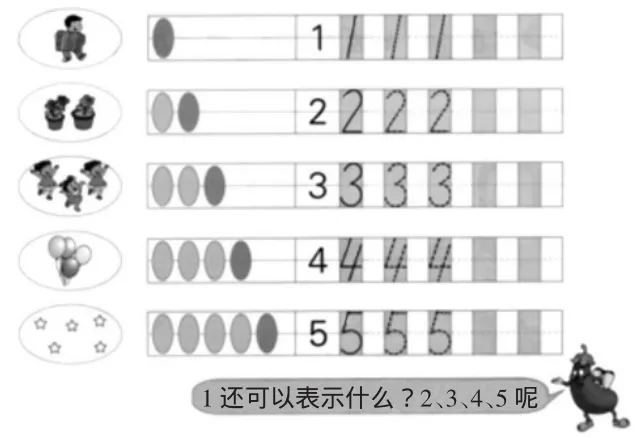
例如一年级上册的“认数1~5”,教科书把人类建立数的概念的近万年历史浓缩为四个环节(如图),首先把相关的实物画上一个圈(即看做一个集合),这意味着我们只聚焦于它在量方面的属性,它等价于1粒算珠,算珠比起“一个小朋友拉手风琴”来说抽象多了,但却是实实在在看得见的;再以此为桥梁,进一步抽象为符号“1”;正因为“1”是抽象来的,所以它具有广泛的代表性,“1还能表示什么?”的追问,就是让学生体会此意义。即便是认识数“1”——不能再简单的数学知识,也必须经历上述四个阶段,更何况其他数学知识呢?所以,抽象性是数学的根本属性,要学习数学,必须经历思考,没有思考就没有数学。
可能有人说,著名的数学大师陈省身先生不是说“数学好玩”吗?抽象的东西,怎么会“好玩”?
说起“好玩”,大家都会想到游戏。大多数成人都有过游戏的经历和体会。一个好玩的游戏,首先是容易入手,不复杂,能很快地玩起来;其次是有点小难度,随着技巧的逐渐熟练,不断有新的进阶等着去挑战,让人废寝忘食。在数学里也有游戏,比如七巧板、华容道、九连环等。七巧板,在国际上被称为“唐图”。拿破仑在滑铁卢兵败之后的流放岁月里常玩七巧板,为什么他没有感到厌倦?因为,七巧板能拼成的图案成千上万!中国科学院院士张景中教授著的《好玩的数学》科普丛书,其中就有吴鹤龄先生《七巧板、九连环和华容道——中国古典智力游戏三绝》一书,剖析了三个经典游戏背后的数学道理。原来,玩智力游戏的本质是在玩数学!
数学知识源于人类的生产劳动实践,但数学科学却源于古希腊人的理性思辨。在人类文明史上,公认的古代文明有古中国、古埃及、古印度、古巴比伦,世人称之为“四大文明发源地”。古中国、古埃及的数学成就都和解决生产劳动中的实际问题紧密联系,而古希腊人通过航海贸易获得了这些数学结果后,在人类历史上破天荒地第一次对这些数学结果进行了理性的哲学考察——为什么它们会如此?相传古希腊的第一个贤者泰勒斯,提出了4个几何命题的一般形式,并设法证明了“等腰三角形底角相等”。公元前387年,柏拉图建立了自己的学院,门口赫然竖立着“不懂几何者禁入”的牌子,能进入学院聚在一起讨论交流的已不可能有真正意义上的劳动者,阳光下、草地上,大家温文尔雅讨论的也不是一个数学结论就能直接解决生产生活中的那个问题,而是交流如何赋予一个数学结论以逻辑性。在这过程中,吸引人的已经不是数学的使用价值,而是纯粹的智力乐趣。因而,英国数学家哈代说:“激励数学家做研究的主要动力是智力上的好奇心,是谜团吸引力。”
陈省身先生说“数学好玩”,这凝聚着一代数学大师自身学习数学、研究数学的切身体会。也正因为陈省身先生是一代数学大师,对数学的理解和感悟也非常人所能比拟,所以这句话从某种意义上也揭示了数学对人的智力挑战的特质,这种特质和数学的抽象性不矛盾,恰恰互为支撑。陈省身先生在天津扶轮中学求学时,乐此不疲地寻找弦切角定理的多种证明方法,撰写了《一个几何定理的十六个证明》,刊登于校刊《扶轮》杂志上,享受的便是思考的乐趣,这是对“好玩不是轻松悠闲,而是享受智力挑战”的有力佐证。
数学穿着抽象的外衣,是个“冰美人”,要走近和走进它,只有一条路,那就是思考起来。数学就其客观意义,本身并无“好玩”之说,要被学习者建立起“好玩”的主观感受,那总结起来不外乎两条:其一,简单有趣;其二,别有洞天。简单有趣,能让学习者容易起步;别有洞天,能让学习者欲罢不能。不少人觉得数学难,所以不爱数学,实际上这是表面现象。数学能让一部分人终生追随,不是因为简单,恰恰是因为“有点难”。
一个教师,不但要从教育学、心理学的角度运用外在的形式吸引学生学习数学,更要通过彰显数学的内在魅力去征服学生。数学,是人类智力的皇冠,吸引人沉醉其中的是可以享受智力的“高峰体验”!一个高明的数学教师,要呈现与儿童的认知水平相匹配的那些数学——能解决又不能随手可得,有信心又需要再作努力。如此,学习的过程犹如陶渊明先生的《桃花源记》:“山有小口,仿佛若有光。便舍船,从口入。初极狭,才通人。复行数十步,豁然开朗。”这样的数学学习过程,经历着“辗转反侧、冥思苦想到石破天惊、豁然开朗”的思考乐趣。由此,学生就走近和走进了数学,只有这样才能感受到数学的理性,才能体会到数学思考的方法,积淀开放的心态,养成回顾的习惯,培育坚韧的品质。
数学从来就是一种文化力量,正如M·克莱因所说:“数学是人类最高超的智力成就,也是人类心灵最独特的创作。音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能扣人心弦,哲学使人获得智慧,科学可以改善物质生活,但数学却能提供以上的一切。”既如此,数学学习还只是学习数学吗?

