飞机颤振模态参数辨识试验的快速滤波算法
王建宏 许莺 熊朝华 徐波
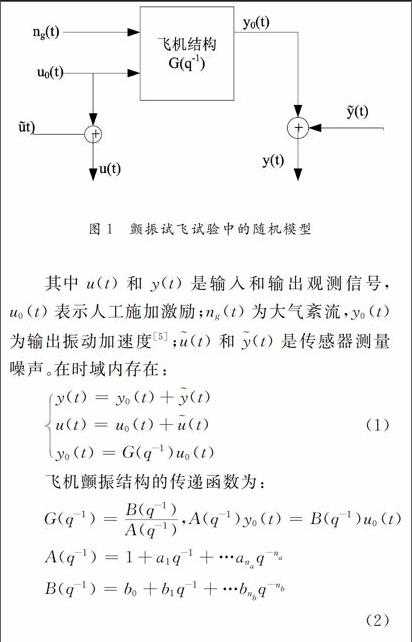

摘 要:研究飞机颤振随机模型中实际输入-输出信号序列的最优滤波估计问题,利用矩阵论中的矩阵因式分解和统计信号处理中的条件期望公式,将由新息过程构成的块Toeplitz矩阵进行三角分解,得到一种有效的递推滤波算法。对于滤波输入输出信号的估计值,推导该算法下的估计误差和方差表达式。最后用仿真算例验证采用滤波后得到的输入输出信号估计值作为飞机颤振模态参数辨识试验的观测信号可得到较为准确的传递函数,进而使得模态参数的辨识也更精确。
关键词:飞机颤振;模态参数;递推滤波;矩阵分解
中图分类号:TP273 文献标识码:A
Abstract:This paper,studied the optimal filtering estimation problem of the actural input and output sequences in the aircraft flutter modal parameter identification experiment. Based on the matrix factor decomposition from matrix theory and conditional expectation formula from statistical signal processing, an efficient recursive filtering algorithm was proposed. It is an innovation based approach that relies on the triangular decomposition of block Toeplitz matrices. We derived the estimation error and covariance expression about the estimation of the filtered input and output sequences. Finally in the simulation, we applied the filered input and output sequences to be the observed signals,which were used in the aircraft flutter modal parameter identification experiment. Then we can obtain the more accurate transfer function and the modal parameters.
Key words:aircraft flutter; modal parameter; recursive filtering; matrix decomposition
1 引 言
目前对飞机颤振模态参数辨识的研究围绕辨识方法及精度展开,根据系统辨识理论体系可知,整个辨识试验应该具有四个研究步骤:试验设计、模型结构辨识、模型参数辨识和模型验证[1]。对于飞机颤振随机模型选择赫伯尔特在飞行动力学下所建立的二维机翼颤振数学模型,因数学模型中的未知参数可转化为模态参数值,对未知参数的辨识求解可采用各种辨识策略;而对飞机颤振试验的试验设计和模型验证研究较少。
试验设计中都是人为地选择人工施加的激励信号,并假设此激励信号足够丰富,能够持续激励颤振随机模型的所有模态被辨识出来[2]。但实际中激励信号的选择往往很难把握,其激励的振幅大小、激励点的位置、采集传感器的布置等都需要斟酌。为此展开对飞机颤振模态参数辨识试验的试验设计是有必要的,在试验设计中需要事先具备关于输入-输出信号的某些先验信息,以此先验信息作用于整个辨识试验的基础,为模态参数的辨识提供充分激励和足够丰富的先决条件[3]。对输入-输出信号先验知识的掌握即为本文所涉及的滤波问题,即采用滤波算法来得到关于输入-输出信号的估计值,以此估计值作为下次辨识试验的激励信号。整个飞机颤振模态参数辨识试验过程可叙述如下:对经典的赫伯尔特二维机翼颤振随机数学模型,首先选择人工施加的激励信号如脉冲信号、阶跃信号和正余弦信号等,利用常用的辨识方法得到颤振随机模型中的未知参数矢量;其次利用得到的参数估计值和已测量得到的输入-输出观测信号采用滤波算法去估计激励信号;再次将估计激励信号又作用于整个飞机颤振随机模型,不断地循环试验,直至未知参数矢量和激励信号的估计值不再发生较大的改变时,则停止循环过程[4]。此时最终得到的参数估计值和激励信号即为最为理想,保证整个辨识试验足够丰富。
2 问题描述
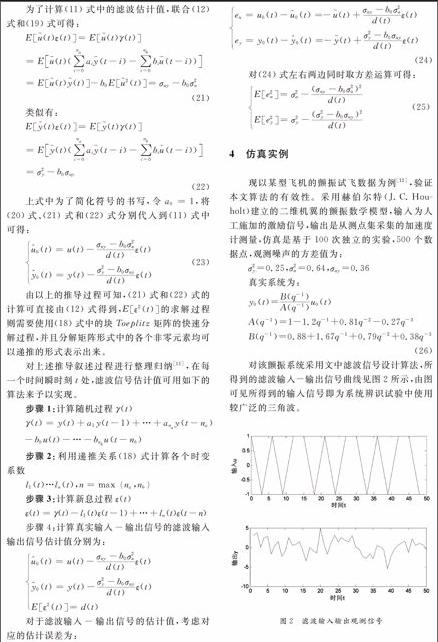
为了验证滤波后的输入-输出观测信号的确比未滤波的输入-输出观测信号更具有实用性。分别将最初的输入-输出观测信号和图2所示的输入-输出观测信号应用于原颤振系统,利用文献[7]提出的全局非线性可分离最小二乘法来辨识颤振系统中的未知参数矢量。将所得到的两组参数估计值代回(24)式的A(q-1)和B(q-1)中,进而构成原颤振系统的传递函数。对于此传递函数的检验,应用matlab中现有的bode plot程序进行仿真。仿真之后的bode plot见图3所示。图3中红色曲线表示原真实系统的频域响应曲线,黑色曲线表示利用滤波之后的输入-输出观测信号得到的系统的频域响应曲线,蓝色曲线表示直接利用最初的输入-输出观测信号得到的系统的频域响应曲线。由图3可见,三条频域响应曲线的相位是一致的,而在振幅上蓝色曲线与红色曲线存在较大的偏离,黑色曲线与红色曲线吻合的较好。此即表明利用滤波之后的输入-输出观测信号能得到较为准确的传递函数,从而同样能得到较为准确的模态参数。
5 结论
本文研究飞机颤振模态参数辨识试验的滤波设计问题,将由新息过程构成的块Toeplitz矩阵进行三角分解,采用条件期望公式建立颤振随机模型中出实际输入-输出信号序列的最优滤波估计,此最优滤波估计即可作为下步系统辨识理论框架系统中的最优输入信号设计。因本文作为飞机颤振模态参数辨识试验中关于试验设计问题的初步研究,对于颤振随机模型的可辨识性,传感器的布局和模型验证等还有待进一步的研究分析。
参考文献
[1] PINTELON R,SCHOUKENS J. System identification: a frequency domain approach [M]. New York: IEEE Press, 2001.
[2] Torston Soderstorn. A covariance matching approach for identifying errors in variables systems[J]. Automatica, 2009, 45(9): 2018-2031.
[3] Torston Soderstorn. Relations betweeen bias-elimizating least squqres, the Frish scheme and extended conmensated least squares method[J]. Automatica, 2009, 45(1): 277-282.
[4] JUAN C. Augero. A virtual closed loop method for closed loop identification[J]. Automatica, 2011, 47(8): 1626-1637.
[5] JUAN C. Augero. Accuracy of linear multiple input multiple output models obtained by maximun likelihood estimation[J]. Automatica, 2012, 48(4): 632-637.
[6] HJALMARSSION H.A geometric approach to variance analysis in system identification[J]. IEEE Transactions of Automatic Control, 2011, 56(5): 983-997.
[7] 王建宏,王道波.基于全局非线性可分离最小二乘法的飞机颤振模态参数辨识[J].振动与冲击,2011,30(2): 210-213.
[8] 王建宏,朱永红,肖绚.飞机颤振模态参数的辅助变量方差辨识及渐近性分析[J].应用科学学报,2012,30(4): 433-440.
[9] Christian Feller. An improved algorithm for combinatorial multiparameteric quadratic programming[J]. Automatica, 2013, 49(5 ): 1370-1376.
[10]PAUL M J Vanden Hof. Identification of dynamic models in complex networks with prediction error methods [J].Automatica, 2013, 49(10): 2994-3006.
[11]Henrik Ohlsson. Identification of switched linear regression models using sum of norms regularization[J]. Automatica, 2013, 49(4 ): 1045-1050.
[12]Anne Van Mulders. Identification of systems with localised nonlinearity: from state space to block structured models[J]. Automatica, 2013, 49(5 ): 1392-1396.

