一种基于超声和射频融合的无线传感器网络网格定位方法*

姜 华， 何风行， 陈文权， 毛 嘉， 苑广欣

(中国科学院 上海高等研究院 城市公共安全中心，上海 201210)

一种基于超声和射频融合的无线传感器网络网格定位方法*

姜 华， 何风行， 陈文权， 毛 嘉， 苑广欣

(中国科学院 上海高等研究院 城市公共安全中心，上海 201210)

提出了一种基于超声和射频融合的网格定位方法。首先对射频的无线信号强度进行筛选，采用压缩感知方法进行粗定位。然后基于粗定位结果对超声测量的计时结果进行评价和加权，以抵抗局部非视距(NLoS)环境影响。之后再迭代时进行进一步精细定位与超声计时结果的评价加权，直至达到终止条件。测试结果显示：所提出的融合定位方法的定位精度优于经典的CHAN算法，在实际测试中取得较好的定位性能。

无线传感器网络； 融合定位； 压缩感知； 网格定位

0 引 言

室内复杂场景下的目标定位问题越来越引起学者关注[1,2]，由于室内不具有GPS信号覆盖，基于无线传感器网络(WSNs)的系统是解决室内目标定位问题的主要方法[3～5]，其中基于射频的接收信号强度(RSS)[2～5]和超声波[6,7]是常用的定位手段， RSS定位成本低廉、部署方便，但是定位精度较差，一般在m级；室内超声定位精度较高，文献[6]在室内无遮挡的情况下达到了10 cm以内的定位精度，但是由于室内复杂环境的限制，受非视距(NLoS)影响较为严重。

本文提出了一种基于超声和射频融合定位的方法，以抵抗室内复杂环境的影响。首先将基于RSS的定位问题转换为压缩感知问题，得到粗定位结果，然后根据粗定位结果对超声测量结果进行筛选，消除局部NLoS环境影响，根据优选结果迭代进行超声网格精细定位。测试结果显示：本文提出的方法具有较好的定位效果。

1 系统总体设计

1.1 系统模型

系统模型如图1所示，设需要定位的区域为室内一矩形区域，将此矩形区域划分为N个网格。此区域中移动目标周期性发射射频信号和超声信号，在区域周围布设M个传感器节点，可接收超声和射频信号，每个传感器节点的位置为已知。传感器节点将信号测量结果(RSS值和到达时间(ToA)值)发送给融合中心。融合中心运行网格融合定位算法，计算出目标位置。

图1 采用超声和射频融合的网格定位系统模型

1.2 算法架构

超声和射频融合定位算法的整体架构如图2所示，首先采用Fisher准则进行RSS测量结果筛选，然后压缩感知方法进行RSS粗定位，根据粗定位结果和ToA结果匹配、评价、加权，进行超声信号的网格精细定位。

图2 超声和射频融合定位算法的整体架构

2 射频信号网格粗定位压缩感知算法

2.1 压缩感知

假设已知测量矩阵Φ∈RM×N(M≪N)和某未知信号X∈RN在采用该测量矩阵时的线性测量值Y∈RM

YM×1=ΦM×NXN×1.

(1)

Y也可以看作信号X在测量矩阵Φ下的线性投影。压缩感知主要解决的问题是由测量结果Y重构信号X。由于X的维数远大于Y的维数，这是一个欠定线性方程组求解问题，有无穷多解。但是,压缩感知理论证明，如果信号X是K稀疏的，并且Y与Φ满足一定条件，信号X可以由测量值Y通过求解l1范数最小的最优化问题精确重构[8,9]

X=argmin‖X‖1,s.t.ΦX=Y.

(2)

2.2RSS测量结果筛选

由于室内无线信道受多径等因素影响，空间某一位置的RSS测量结果在一定范围内波动。为了去除RSS异常值带来的定位偏差，在离线情况下，采用Fisher准则对RSS结果进行评价[10]，排除掉异常传感器节点带来的影响

(3)

式中φi,j为传感器节点i接收到的位于参考点j的目标发射的RSS值，分子的含义为RSS在不同参考点测量值的变化幅度，衡量了传感器节点区分不同参考点的能力，数值越大区分度越强。Δi,j为传感器节点在不同时刻接收同一位置参考点RSS值的方差，分母的含义为衡量了传感器节点RSS的时间稳定性，分母越小表示测量结果在时域上更稳定。

2.3 压缩感知问题建模

文献[5]建立了压缩感知定位模型。系统的压缩采样过程可用式(4)描述，xn=0或1(1≤n≤N)，当第n个网格中有目标时,xn=1;否则,xn=0。传感器的测量结果Y为测量矩阵与稀疏向量X的乘积，其物理意义为传感器节点ym(1≤m≤M)接收到的目标信号强度。

(4)

式(4)简记为

YM×1=PM×NXN×1.

(5)

根据上面的模型，基于RSS的目标定位问题转换为压缩感知问题。可以运用l1范数最小等重构算法求出问题的解。测量矩阵P的生成有两种办法：一种方法是采用信号衰减模型生成测量矩阵，适用于室内环境理想的情况；另一种方法是根据实际测试结果得到测量矩阵，适用于室内环境复杂的情况。本文采用后一种方法，根据各网格参考点中的目标信号进行实际测试得到测量矩阵。

2.4 压缩感知贪婪匹配重构算法

压缩感知重构算法可分为以下五类[11]：贪婪追踪法、凸松弛法、贝叶斯法、非凸优化法和穷举法。贪婪追踪法和凸松弛法有较完备的理论基础，成为应用最多的两种方法。凸松弛法性能比较稳定，但计算量大；贪婪追踪法实现简单，运行时间短，但需要一定量的先验信息。本文采用贪婪匹配算法[12]，定位算法设计如下：

输出：重构信号X

1)初始化，匹配余量y′=y，重构结果X=0，支撑集为全部网格N；

2)求解如下优化问题，其中,z为稀疏度为1的列向量(只有第i个元素的值为zi，其余元素均为0)

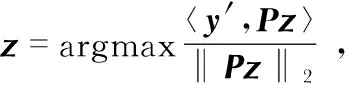
3)如果z≠0，则y′=y′-Pz，X=X+z，支撑集减去当前网格，跳转到第2步；

4)信号重构结束，重构结果为X。

上述算法通过求余量y′与测量矩阵中各原子的相关性进行信号逼近和余量更新，保证了每次迭代的最优性，迭代次数最大为N。

3 超声信号网格精细定位算法

3.1 对抗局部NLoS影响的超声节点信号筛选

4.家庭教育方式不当。家长过度的唠叨、责骂、猜疑、嘲讽甚至动之以拳脚或不切实际的加大学习量，使学生有可能产生抵触情绪进而演化为厌学情绪。

超声的传播速度约为340 m/s，超声飞行时间(time of flight,ToF)测量精度可以达到μs级，所以,超声定位精度一般明显高于RSS定位。但由于室内环境的复杂性，NLoS对超声定位结果有很大影响。文献[13]对室内环境下超声波传输特性进行了详细研究，分类如下：

1)无遮挡情况(视距传播):如图3中的目标和传感器节点B1，这种情况下ToF测量误差小于0.15 %，主要是温差对声速的影响，如果温度相差5 ℃，误差约为1 %。

2)轻微遮挡(远处):如图3中的目标和传感器节点B2，这种情况下误差具有一定的随机性，最大误差约为5 %。

3)较严重遮挡(近处):如图3中的目标和传感器节点B3，这种情况下误差和遮挡物距离非常相关，最大误差可能达到10 %～100 %。

4)严重遮挡(完全遮挡):如图3中的目标和传感器节点B4，这种情况下无ToF测量结果，或为噪声、干扰触发的无意义的结果。

图3 室内环境对超声传输的影响

本文假设受NLoS影响的是少数传感器节点，大部分传感器节点和目标之间是视距路径。利用RSS粗定位结果，对超声信号的ToA结果进行评价和加权，对抗局部NLoS影响

(6)

式中 wi为传感器节点i的权重，x为RSS粗定位结果与传感器节点i的ToA结果之间的偏差。当偏差小于阈值a(约为网格大小)，对应为视距传播情况，评价结果为“good”，权重为1；当偏差大于阈值b(约为2倍网格大小)，对应为严重遮挡情况，评价结果为“bad”，权重为0；当偏差介于a～b之间，评价结果为待定，按照式(6)计算权重值，介于0～1之间。

3.2 超声信号网格定位方法

超声信号网格定位方法如图4所示，由粗到精的迭代进行网格定位。网格大小的初值取为RSS粗定位网格大小，面积每次缩小为1/4。

图4 超声信号网格定位方法

目标函数为加权的定位偏差最小

(7)

上述目标函数最优化求解迭代进行。初值根据粗定位结果得到，wi为权重值，di为测量结果得到的距离值，d0为根据上次迭代定位结果得到的距离值。终止条件为达到期望精度或目标网格内有效ToA结果小于阈值。

4 实验验证

4.1 测试平台

实验室环境下基于自研硬件平台进行了实际测试，图5(a)为传感器节点，每个节点包含射频收发模块与数据处理模块，数据处理模块采用意法半导体ARMCortexM3系列STM32F103VG处理器，射频模块采用德州仪器CC1101射频芯片。每个节点含2只MIC，相距1m。图5(b)为超声和射频发射节点，每个节点含3只超声扬声器，互成120°夹角。

图5 超声和射频融合定位硬件平台

4.2 定位性能

实验室大小为8m×12m，由于实验台、机柜、人员走动，存在NLoS路径。在墙壁上部署了6个传感器节点，如图6。参数设置为：粗定位网格大小为2m。超声评价阈值的初值a=1.5m，b=3m。人员移动路线和定位结果见图6。定位偏差最大为50cm左右，原因是由于该处超声信号被严重遮挡。

图6 超声和射频融合定位结果

对本文提出的融合算法和经典的CHAN算法的定位性能进行了对比，如图7所示。在相同测试环境下(有2个节点存在遮挡)，本文算法的定位误差小于15cm，CHAN算法的定位误差小于45cm。不同定位环境下的定位效果对比如表1所示。本文算法采用射频和超声融合，对超声信号进行筛选、加权，剔除了局部NLoS影响，取得了更好地定位效果。

图7 累积误差分布对比

表1 不同室内环境情况下定位精度对比

5 结 论

室内定位有着重要和广泛的应用场景。本文利用超声和射频融合进行无线传感器网络网格定位，系统易于部署，测试结果表明：本文提出的融合定位方法的定位精度优于经典的CHAN算法，在具有局部NLoS路径的室内实际环境下取得了较好的定位效果。

[1] 高云峰，周 伦，吕明睿,等.自主移动机器人室内定位方法研究综述[J].传感器与微系统,2013,32(12):1-6.

[2] Paramvir Bahl,Venkata N Padmanabhan.RADAR:An in-building RF-based user location and tracking system[C]∥Proceedings of INFOCOM 2000,Israel,2000:775-784.

[3] Lee Hojae,Lee Sanghoon,Kim Yeonsoo,et al.Grouping multi-duolateration localization using partial space information for indoor wireless sensor networks[J].IEEE Transactions on Consumer Electronics,2009,55(4):1950-1958.

[4] 孙 妍，陶正苏，陈德富.基于无线传感器网络的室内精确定位算法[J].传感器与微系统,2009,28(5):99-102.

[5] 何风行,余志军,刘海涛.基于压缩感知的无线传感器网络多目标定位算法[J].电子与信息学报,2010,23(3):347-353.

[6] 韩 霜，罗海勇，陈 颖，等.基于TDOA的超声波室内定位系统的设计与实现[J].传感技术学报,2010,34(3):716-721.

[7] 刘 君，吴建国，褚曦丹.Cricket室内定位系统的研究与改进[J].计算机技术与发展,2011,21(5):206-209.

[8] Donoho D L.Compressed sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[9] Candes E,Romberg J,Tao T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency informa-tion[J].IEEE Transactions on Information Theory,2006,52(2):489-509.

[10] 冯 辰.基于压缩感知的RSS室内定位系统的研究与实现[D].北京：北京交通大学，2011.

[11] Tropp J A,Wright S J.Computational methods for sparse solution of linear inverse problems[C]∥Proceedings of the IEEE,2010,98(6):948-958.

[12] Zhang Bowu,Cheng Xiuzhen.Sparse target counting and localization in sensor networks based on compressive sensing[C]∥INFOCOM,Shanghai,China,2011:10-15.

[13] Casas R,Marco A,Guerrero J J,et al.Robust estimator for non-line-of-sight error mitigation in indoor localization[J].European Association for Signal Processing Journal on Applied Signal Processing,2006,6(2):156-163.

A method of grid localization in WSNs using fusion of ultrasonic and radio frequency*

JIANG Hua, HE Feng-hang, CHEN Wen-quan, MAO Jia, YUAN Guang-xin

(Center for Urban Public Safety,Shanghai Advanced Research Institute,Chinese Academy of Sciences,Shanghai 201210,China)

A grid localization method using fusion of ultrasonic and radio frequency is proposed.Firstly,wireless signal strength is screened for coarse localization by compressed sensing model.Then,timing results of ultrasonic measurement are evaluated and weighted based on coarse localization results,to conquer effect of local NLoS environment.Further,fine localization is performed and weighted by evaluation of ultrasonic timing result by iteration algorithm,until the termination condition is reached.Test results show that the proposed method achieves better localization precision than classical CHAN algorithm,and better localization property is achieved in practical test.

WSNs; fusion localization; compressed sensing; grid localization

10.13873/J.1000—9787(2015)03—0024—04

2014—07—09

国家电网公司科技计划资助项目

TP 393

A

1000—9787(2015)03—0024—04

姜 华(1977-)，男，山东威海人，博士，副研究员，研究方向为无线传感器网络、物联网。