一种基于双随机相位编码的光学加密系统设计
王彩玲,王洪伟,刘瑞香
(1.西安石油大学计算机学院,陕西 西安 710065;2.中国人民武装警察部队工程大学,陕西 西安 710086)
·光电技术与系统·
一种基于双随机相位编码的光学加密系统设计
王彩玲1,王洪伟2,刘瑞香1
(1.西安石油大学计算机学院,陕西 西安 710065;2.中国人民武装警察部队工程大学,陕西 西安 710086)
针对于有加密需求的监控领域,图像数据剧增对加密算法提出严峻考验。复杂的加解密算法将会增大运算开支,最终影响视频传输的实时性能。本文根据视频加解密要求,提出在视频监控领域进行光学加解密并设计了基于双随机相位编码的单通道加解密光学系统。该光学系统加解密速度和光速相等,加解密时耗几乎为零,在高清视频迅速普及的未来将会产生重要的应用价值,在军事加解密领域将有着广阔的应用前景。
光学加解密;双随机相位编码;视频加密;傅里叶变换
1 引 言
随着科学技术的发展以及网络通信设施基础的日渐完善,网络信息安全与国家安全、社会稳定关联越来越强。信息技术得到了广泛运用,举足轻重的地位也日益凸显[1]。同时,信息通信的蓬勃发展也对信息安全提出了更高的要求。
近年来,信息通信中的图像侦查技术在各行各业进行了大规模开发应用,随着软硬件的快速发展,高清时代已经来临。目前视频监控图像数据量越来越大,视频监控系统覆盖面越来越广,对图像的辨识度的要求也越来越高,高清化成为了未来的一种发展趋势[2]。但是由于监控领域的某些加密需求,图像数据量的增大将会对加密算法提出严峻的考验,图像尺寸的增大将会严重增加加密算法的开支以及加解密的运算时间[3-5],因此进行快速有效地加解密算法的研究就成为了一项重要的研究方向。
本文根据视频加密要求,提出在视频监控领域进行光学加解密的思想,在此基础上设计了基于双随机相位编码的加密光学系统[6],同时根据光路可逆原理就实现了光学解密。光加密的加解密速度和光速相等,因此在加解密系统中,将加解密时间降低为零,极大提高了视频传输性能。在高清视频迅速普及的未来将会产生重要的应用价值,在军事加解密领域将有着广阔的应用前景。
2 光学加解密系统介绍
光学加解密系统具有处理速度快,加密维度高、分辨率高等优点,因此基于光学信息处理的图像加密技术已经成为国内外的研究热点。本系统经过光学系统的傅里叶变换以及反变换并辅以两个随机相位板进行加密,加密后的图像接近均匀随机噪声,所以加密后的图像在未知解密密钥的情况下几乎不可能恢复出原来的真实图像。
光学加解密系统如图1所示,目标光线通过光学成像镜头成像后进入光学加密镜头,加密后在CCD成像感光芯片上将加密后的光学成像记录下来,并通过有线或者无线网络传输出去。
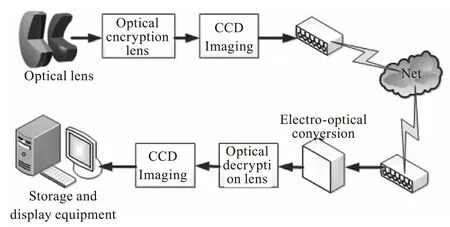
图1 光学加解密系统框图
解密是其逆过程,将加密镜头倒置即可作为解密镜头使用。网络传输回来的图像经过电光转换后,经过光学解密镜头在CCD成像芯片上成解密后的真实图像,然后通过电脑服务器进行存储,并用终端设备将图像予以显示。
3 双随机相位编码技术
为防止加密后的图像被破译,将加密后的图像尽可能地趋于均匀的随机噪声,本文使用双随机相位编码技术,利用傅里叶变换将图像变换到频率域后进行一次置乱,再利用傅里叶反变换,然后再进行一次置乱,便可得到一幅接近于均匀噪声的图像。这就是双随机相位编码技术[7-9]。
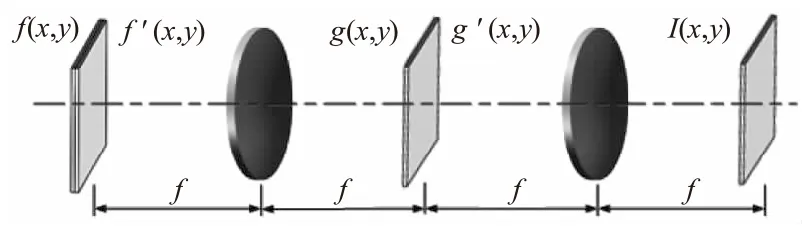
图2 双随机相位编码技术光学实现示意图
该技术采用如图2所示的4-f系统来实现:先把一块随机相位板放在光学系统的输入位置,对图像f(x,y)的空间信息进行置乱后图像变为f′(x,y),然后经傅里叶变换后变为g(x,y),然后再用一块相位板对傅里叶变换后的频谱图像再进行一次信息置乱图像变为g′(x,y),然后再经过一次傅里叶反变换得到统计特性随时间平移不变化的平稳白噪声I(x,y)。f(x,y)既可以是振幅型的实函数,也可以是经过预编码为相位型的虚函数。如果经过预编码的话,破译将会更加困难,并能提高图像解密的抗噪声能力。
将随机相位板中的p(x,y)与b(u,v)分别为[0,1]之间均匀分布的随机数列,其中u,v分别为傅里叶空间坐标,则加密后的图像可以表示为:
(1)
因为光路可逆,所以解密只是加密的逆过程。由于接收解密图像时用的光强敏感器件,因此如果f(x,y)是实函数,只需要傅里叶谱平面的加密密钥的复共轭作为解密密钥,而如果f(x,y)是虚函数,则需要两块随机相位板对应的复共轭作为解密密钥。
在光学加密中所使用的随机相位板具有加密秘钥的作用,所以要求其所具有的分辨率极高,在数平方毫米的面积上分布着上百万个像素,因而密钥空间非常大,在不得知密钥相位分布的情况下,很难通过盲目反卷积运算恢复加密图像,因而该算法具有较高的安全性。
4 彩色图像编码
为了降低光学加密系统的体积以及成本,本文采用三色复合光栅对彩色图像进行分离,将彩色图像分解成红、绿、蓝三个分量的灰度图像。然后利用三色复合光栅将彩色图像编码成灰度图像,从而只需对一路编码后的图像进行光学加解密,简化了系统。
三色复合光栅是一种特殊的空间光调制器[10-11],由横向、竖向、135°方向三个Ronchi子光栅叠加组成。目前利用计算机辅助制造技术在一块材料上即可制作。其结构如图3所示。三个Ronchi子光栅能分别透过红色、绿色、蓝色,并对其进行空间频率调制,调制后衍射光波按子光栅的方向进行传播。从而使一级频谱分别照射到各自的位置上,实现各衍射一级频谱的分离。
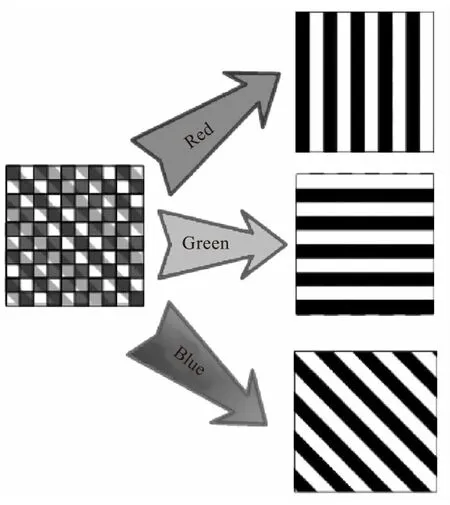
图3 三色光栅组成结构
彩色图像编码的光学系统如图4所示,用三色光栅对彩色图像进行灰度编码,然后再进入加密光学系统。

图4 彩色图像编码光学系统
一副彩色图像可以表示为:
fcolor(x,y)=fr(x,y)+fg(x,y)+fb(x,y)
(2)
其中,r、g、b分别表示为彩色图像中的红、绿、蓝的分量。
三色复合光栅的透过量可以表示为:
g(x,y)=gr(x,y)+gg(x,y)+gb(x,y)
(3)
彩色图像经过三色复合光栅编码后得到的灰度编码可以表示为:
f(x,y)=fr(x,y)gr(x,y)+fg(x,y)gg(x,y)+fb(x,y)gb(x,y)
(4)
5 加解密系统光学设计
光学加解密系统的核心是傅里叶变换透镜组的设计,其性能的好坏对光学加解密的结果将产生直接的影响。目前较为常用的有两种傅里叶镜组结构主要由单组元型和双远距型[12-13]。单组元结构又包括单片型、双分离或双胶合,其结构简单、造价低,但系统较长、像质差。双远距型包括对称型和非对称型,其结构紧凑、像质较好,但结构复杂、成本较高。鉴于此,本文使用双远距型并结合光学加解密系统的实际需求,设计了傅里叶变换透镜。
傅里叶变换透镜的主要参数有相对孔径、焦距和能处理的最高空间频率Nmax相当于分辨率。而傅里叶变换透镜的最高空间分辨率Nmax必须大于图像传感器的最高空间频率(ξmax,图像传感器的最高空间频率由传感器像元大小决定(即线对分辨率)。经初步选型后初步确定使用三片式双胶合透镜作为初始结构,图 5为所设计傅里叶透镜的光路图。

图5 傅里叶镜组光路图
由于傅里叶变换透镜是个小像差系统,所以可以通过调制传递函数(MTF)、波相差(PTV)来评价光学系统的成像质量。由图 6可见傅里叶变换透镜的各视场的传递函数曲线与衍射极限几乎重合,并在在60 lp/mm处的MTF值达到了0.78以上。图 7为系统的波前图,由图可见系统的PTV值为0.1519λ,小于瑞利判据的0.25λ标准。因此可以看出系统已经达到了较好的成像质量。

图6 调制传递函数MTF曲线

图7 波前图
傅里叶镜组设计好之后,就可对整体加解密系统进行设计了,光学加解密系统设计好之后光路图如图 8所示。光路经过折叠之后系统体积相对紧凑。

图8 光学加解密光学系统
6 模拟仿真结果分析
根据上述方法,在Matlab中进行仿真计算,计算结果如图 9所示,其中图 9(a)是一副大小为512×512一幅彩色图像,图 9(b)是将彩色图像编码后的图像,图 9(c)是编码后图像的频谱图像,图 9(d)是采用双随机相位加密技术对图 9(b)加密后的接近于白噪声的图片,图 9(e)是解密后得到的编码灰度图像,图 9(f)是解码后的彩色图像。

图9 光学加解密仿真结果
由图可见,经过仿真计算,彩色图像经过编码以及光学加解密之后图像基本完全复原。
7 结 论
本文采用三色复合光栅编码技术以及双随机相位加密技术实现了对一个通道将彩色视频图像进行加解密,简化了系统结构、降低了制造成本、提高了系统适用性。由于光学加解密技术是在视频链路的最前端以及最后端实现的,不涉及中间的编码和传输,所以本系统容易实现、具有通用性,并且对现有视频链路改造简单。同时由于采用了两个相位因子是随机的相位板,在没有掌握随机相位板具体分布的情况下解密原图像时相当困难的,从而保证了视频传输的安全性。
[1] WU Kenan,HU Jiasheng,WU Xu.Optical encryption for information security[J].Laser & Optoelectronics Progress,2008,45(7):30-38.(in Chinese) 吴克难,胡家升,乌旭.信息安全中的光学加密技术[J].激光与光电子学进展,2008,45(7):30-38.
[2] LIN Dong.HD technology:the development direction of digital video surveillance system[J].China Security & Protection,2009,Z1:38-39.(in Chinese) 林冬.高清化:数字视频监控系统发展方向[J].中国安防,2009,Z1:38-39.
[3] ZHANG Kun,GAN Xiaoting.Image encryption algorithm based on tangent-delay ellipse reflecting cavity map system and lifting wavelet transform[J].Laser & Infrared,2013,43(5):573-577.(in Chinese) 张坤,甘小艇.TD-ERCS混沌系统和提升小波相结合的图像加密方法[J].激光与红外,2013,43(5):573-577.
[4] YANG Fengxia.Encryption of compressed image based on logistic mapping[J].Laser & Infrared,2013,43(5):565-568.(in Chinese) 杨凤霞.基于Logistic映射的压缩图像加密算法[J].激光与红外,2013,43(5):565-568.
[5] YANG Fengxia.Image grouping encryption algorithm based on Logistic mapping and z-mapping[J].Laser & Infrared,2014,44(1):103-107.(in Chinese) 杨凤霞.基于Logistic映射和z-映射的图像分组加密算法[J].激光与红外,2014,44(1):103-107.
[6] LIU Yi,WANG Shipan.Cryptographic recording of hologram nestling closely to phase plate[J].Laser Journal,2000,02:34-35.(in Chinese) 刘艺,王仕璠.位相板紧贴全息图的加密记录[J].激光杂志,2000,02:34-35.
[7] PENG Xiang,TANG Hongqiao,TIAN Jindong.Security analysis of double random phase encoding optical encryption system[J].Acta Physica Sinica,2007,56(5):2629-2636.(in Chinese) 彭翔,汤红乔,田劲东.双随机相位编码光学加密系统的唯密文攻击[J].物理学报,2007,56(5):2629-2636.
[8] PAN Wu,DING Yunbo,YANG Jing,et al.Security analysis of double random phase encoding optical encryption system[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2008,01:74-77.(in Chinese) 潘武,丁云波,杨静,等.双随机相位编码光学加密系统的安全性分析[J].重庆邮电大学学报:自然科学版,2008,01:74-77.
[9] LIU Zhengjun,LIU Shutian.Image encryption encoding scheme based on anti-commutation rule[J].Infrared and Laser Engineering,2006,S4:64-67.(in Chinese) 刘正君,刘树田.基于反对易关系的图像加密编码方案[J].红外与激光工程,2006,S4:64-67.
[10]GAO Lijuan,YANG Xiaoping,LI Zhilei,et al.A method of color image single-channel encryption[J].Acta Physica Sinica,2009,58(2):1053-1056.(in Chinese) 高丽娟,杨晓苹,李智磊,等.一种单通道彩色图像加密方法[J].物理学报,2009,58(2):1053-1056.
[11]ZHANG Baoying.Study of digital frequency in tricolor grating color photography[J].Laser & Optoelectronics Progress,2010,47(3):030502.(in Chinese) 张宝颖.三色光栅彩色摄影数字化频率的研究[J].激光与光电子学进展,2010,47(3):030502.
[12]FANG Jingyue,ZHOU Pu,KANG Qiang.Encrypting optical image based on compound encoding on space-fractional domain[J].Infrared and Laser Engineering,2005,34(3):345-347,372.(in Chinese) 方靖岳,周朴,康强.基于空域-分频域混合编码的光学图像加密[J].红外与激光工程,2005,34(3):345-347,372.
[13]ZHU Congxu,CHEN Zhigang.Image encryption with chaotic mask encoding virtual-optics imaging system[J].Infrared and Laser Engineering,2006,S4:73-78.(in Chinese) 朱从旭,陈志刚.基于混沌掩码虚拟光学成像系统的图像加密[J].红外与激光工程,2006,S4:73-78.
Optical encryption system design based on double random phase encoding
WANG Cai-ling1,WANG Hong-wei2,LIU Rui-xiang1
(1.The School of Computer Science Xi′an Shiyou Universicy,Xi′an 710065,China;2.Engineering University of APF,Xi′an 710086,China)
The increase of image data presents a serious challenge for the encryption algorithm in video surveillance.Complex encryption and decryption algorithm will increase the cost of calculation,which influences real-time performance of video transmission.In this paper,according to encryption and decryption requirements of the video,optical encryption and decryption is proposed in the field of video surveillance,and optical encryption and decryption system was designed based on double random phase encoding.The calculation speed of encryption and decryption is equal to the speed of light.Therefore,the spent time is almost equal to zero.The optical system will generate important value with the rapid popularity of high definition video and have broad application prospect in the domain of military encryption and decryption.
optical encryption and decryption;double random phase encoding;video encryption;Fourier transform
国家自然基金(No.41301382,41301480)资助。
王彩玲(1984-),女,讲师,博士,主要从事光学成像技术方面的研究。E-mail:azering@163.com
2014-10-09;
2014-11-04
1001-5078(2015)07-0834-05
TN29
A
10.3969/j.issn.1001-5078.2015.07.022

