重构X射线脉冲星信号的纯数值模拟新算法*

桂先洲，黄森林，孙 晨

(国防科技大学航天科学与工程学院，湖南长沙 410073)

空间探测中如何实现深空探测器的完全自主导航是一个头等难题。目前应用的导航方式主要有天文导航、卫星导航、惯性导航和地基导航。传统的天文导航依赖近天体进行定位，定位精度不高，且操作复杂［1-3］。近地空间航天器可以利用卫星导航系统实现较精确导航，但卫星导航系统本身需要定位，自主性较差。惯性导航系统的误差累积效应严重，不能单独进行长时间的导航，一般作为组合导航的辅助导航手段［4］。地基导航系统通常使用雷达测距和光学跟踪进行定位，但对于深空导航，其定位的横向精度差，且完全依赖地面站，地面站要进行大量的运算［5］。X射线脉冲星是一类高速旋转，并发射X射线的中子星，探测器接收到的X射线信号体现为周期性的脉冲，其周期稳定性可以媲美现在精度最高的原子钟［6］。X射线脉冲星是天然的导航信标，脉冲星导航是目前最具潜力实现深空自主导航的技术。

目前对X射线脉冲星导航的研究主要集中在定位方面［7-8］，关键之一是脉冲相位估计［9-10］。脉冲相位估计算法的仿真分析需要以X射线脉冲星光子的到达时间作为实验数据［11］。由于观测数据的精确相位未知，不能进行误差分析;而重构的X射线脉冲星信号其相位已知，因此利用模拟算法重构的脉冲星信号进行相位估计算法仿真十分必要。

X射线脉冲星信号的模拟有两种方法，实物模拟和纯数值模拟。文献［12］采用实物模拟方法，该方法成本高、精度低。文献［13］提出使用可见光源和单光子探测器搭建实物模拟系统，提高系统的灵活性和精度。

文献［14］提出的模拟方法为纯数值模拟，该方法成本低、灵活性强，但模拟过程将非线性泊松过程的强度函数分段近似为恒定值，极大地降低了模拟的精度。文献［15-16］都基于反函数构建了数值模拟算法的数学模型，但前者并没有进一步阐述反函数如何求解，后者则是对模型进行了近似化简，避免了反函数的求解，这导致了信号模拟的精度不高。

本文提出一种基于精确光子流量函数的纯数值X射线脉冲星信号的模拟算法。该算法的数学模型基于反函数建立，脉冲轮廓通过分段线性函数拟合，从而反函数易求。然后以χ2拟合优度检验作为验证方法，对信号模拟算法的有效性进行定量验证。最后比较了三种信号模拟算法，并将本文提出的算法生成的观测脉冲轮廓与标准轮廓比较，对信号模拟算法的有效性进行验证。

1 信号模拟算法

1．1 信号模型

X 射线脉冲星发射X射线光子是一个随机过程，探测器记录的光子到达时间则服从非齐次泊松分布。设光子流量函数为λ(t)，该函数表征单位时间到达探测器的光子数目，标准脉冲轮廓函数的表达式与光子流量函数相同。观测时段为(t0，t)内到达的光子数目为(t，s)内到达的光子数目，则Nts服从参数为的泊松分布，在(t，s)内到达 k 个光子的概率为:

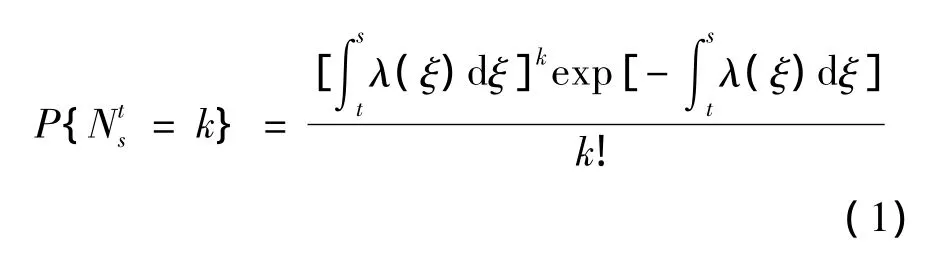
其期望和方差为

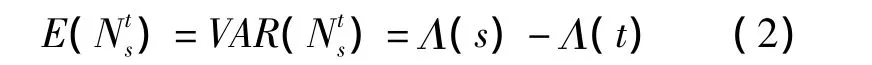
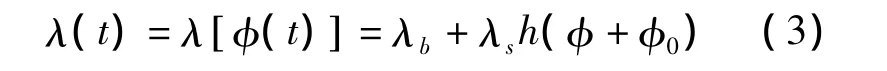
其中，φ+φ0为t时刻对应的相位，φ0为信号的初始相位和 λs分别是背景辐射密度和脉冲星辐射平均密度，单位与λ相同(ph/s，即每秒接收的光子数目)，这两个量可从天文观测数据得知。h(φ)以1为周期，且满足归一化条件

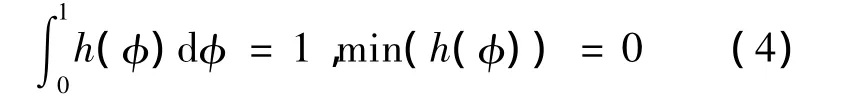
当 φ ＞1时，h(φ)=h(φ -n)，n=floor(φ)，n是不大于φ的最大整数。

1．2 脉冲轮廓函数

脉冲轮廓可由历元折叠方法构建。X射线脉冲星的信号由时间序列组成，在信号周期已知的前提下，可以将若干个周期的信号折叠到一个周期内。时间序列可表示为{ti}m1，转换方法如式(5)所示。

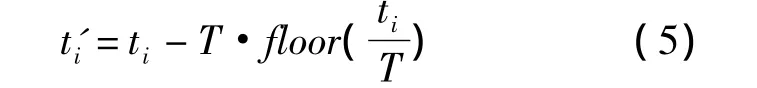
其中，T为信号周期，floor(x)表示不大于x的最大整数。将一个周期划分为Nb个足够小的区间，统计落在每个区间的光子数目ni，每个区间长度为L=T/Nb，共有 Np个周期的数据，则第 i个区间的平均光子流量函数

当观测时间足够长时Np→∞，Nb→∞每个区间的长度L→0，可以得到光滑、近似连续的标准脉冲轮廓。

由式(2)可得

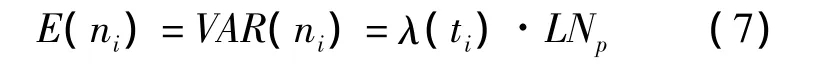
其中ti为第i个时间段的中点，故

1．3 信号模拟算法

X射线脉冲星信号的数值模拟算法可分为两种，一种基于光子数分布率，一种基于分布函数的反函数。

1．3．1 基于光子数分布率的信号模拟算法

在(t，s)内到达k个光子的概率P{Nts=k}可由式(1)计算，将一个周期划分为Nb个足够小的区间，每个区间称为一个时间仓(bin)，第i个时间仓内的光子数记为Ni，其分布率可记为

k 0 1 … ＞p P{Ni=k} P0 P1 … 1-∑p i=1 Pi

当时间仓足够小时，每个时间仓中的光子数目取值基本为0或1。对于某一特定长度的时间仓，大于p个光子数的事件为小概率事件，可以将其光子数近似为p。

根据分布律可以利用随机数生成每个时间仓内的光子数目，以时间仓的中点作为该时间仓内光子的到达时刻。

1．3．2 基于反函数的信号模拟算法

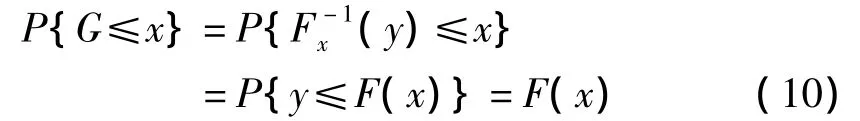
X射线脉冲星信号用光子到达时间表示，因此，其模拟算法可按如下方法导出。

设X射线脉冲星光子的到达时间间隔为x，则x的分布函数与具体的时刻t有关，可用条件分布函数表示为

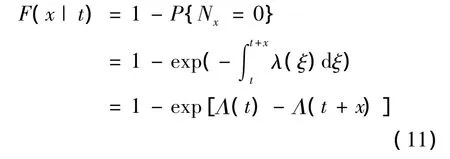
其反函数为

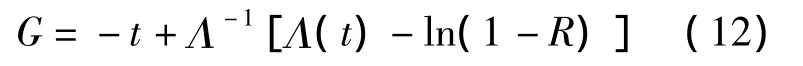
由于R是(0，1)区间上的随机变量，故(1-R)也是(0，1)区间上的随机变量，式(12)可简化为

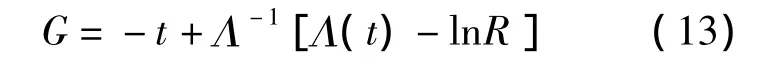
又G为光子到达时间差，t为当前时刻光子的到达时间，故下一个光子的到达时间为

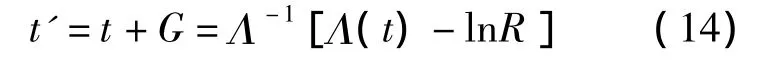
脉冲轮廓λ(φ)的表达式一般并不规则，故使用解析方法不易求出Λ(t)和Λ-1。基于反函数的信号模拟算法之间的区别就在于如何处理Λ(t)和 Λ-1。

1)针对这一问题文献［16］采用了近似模型，当光子到达时刻间隔很小，即δt→0时，

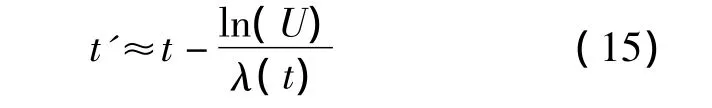
但是当脉冲星光子流量较小时，并不满足δt→0的条件，不能采用上式进行信号模拟。

2)本文采用分段线性函数拟合脉冲轮廓函数λ(φ)。脉冲标准轮廓也是通过历元折叠构建，因此由离散点表示。当利用指数函数或高斯函数等拟合时［17-18］，虽然可以得到平滑的轮廓曲线，但相应的求轮廓函数积分及积分函数的反函数时十分困难。

信号模拟主要是为了分析相位估计算法，轮廓形状会影响相位估计的精度，因此必须针对不同的脉冲星采用其标准脉冲轮廓。但是轮廓是否光滑并不影响结果。因此采用分段线性函数拟合脉冲轮廓是可行的，而且λ(φ)分段可积，Λ(t)的反函数也易求。

设历元折叠的时间仓数目为M，则标准脉冲轮廓的离散点数目为M+1，为了保证离散点可以表示整个周期的轮廓，使第一个点的相位为0，最后一个点的相位为1。第 i个离散点表示为，括号中第一项为相位，第二项为光子流量。线性函数拟合的脉冲轮廓可表示为

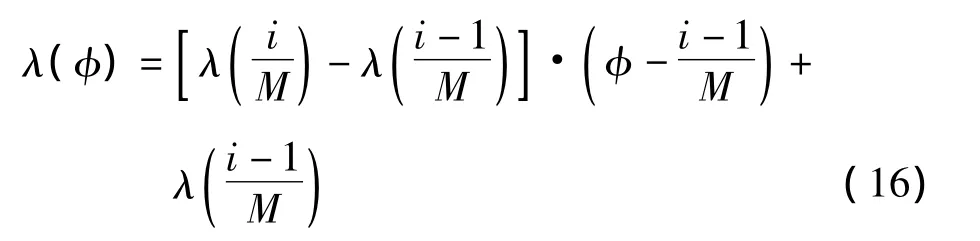
由于式(16)是线性的，所以Λ(t)易求，而Λ(t)是关于相位φ的二次函数，故Λ-1可以通过求解二次方程得到，为了简化计算，还可以通过内插值得到近似解。值得一提的是，这里的近似解是利用精确模型确定光子到达时刻范围后取近似值，基本不会影响后续信号的模拟，而式(15)则是对模型取近似，然后用近似的模型生成光子到达时刻，该时刻可能偏离精确模型计算值较远，从而影响后续信号的生成。

图1 crab脉冲星标准脉冲轮廓Fig．1 Standard template pulse profile of crab pulsar

2 实验与结果分析

2.1 泊松过程检验

本节分析1．3．2节中提出的基于分段线性函数拟合的标准脉冲轮廓的信号模拟算法，采用χ2拟合优度检验法验证生成的信号是否服从泊松分布。以某一时间段内的X射线光子数a={0，1，2…ai}，i=1，2，3…作为样本，记样本中等于 ai的个数为ni并设a共有k个不同的取值，由式(18)可求得a=ai=i-1的概率pi，样本总数为n=，则皮尔逊χ2统计量为

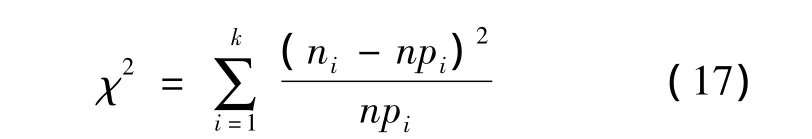
对给定的显著性水平α，检验规则为:

2.2 整段统计

生成25个周期，即1s的观测数据，即t=0，s=1。然后统计1s内观测到的光子数目。皮尔逊χ2统计量的计算为:

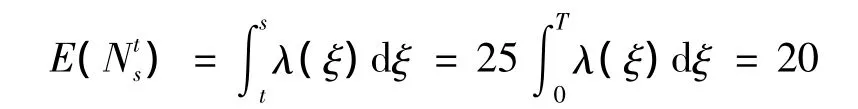
可得

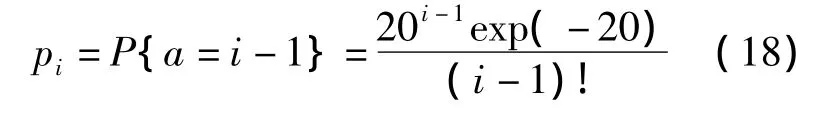
其中，i=1，2，3，…，取 a={0，1，…，48，［49，∞)}，则 k=50，i的最大值为50，记

n50为大于光子数，大于等于49的样本数。

根据式(17)即可计算出χ2。

由信号模拟算法生成5000个样本数据，ni的分布如图2所示，由图可见，在光子数集中在期望值附近，而大于或小于期望达到某一值后，样本数量变为 0。将 ni代入式(17)求得 χ2=24．263 8，又．338 6 故)，说明在一整段时间内产生的光子到达时刻服从泊松分布。

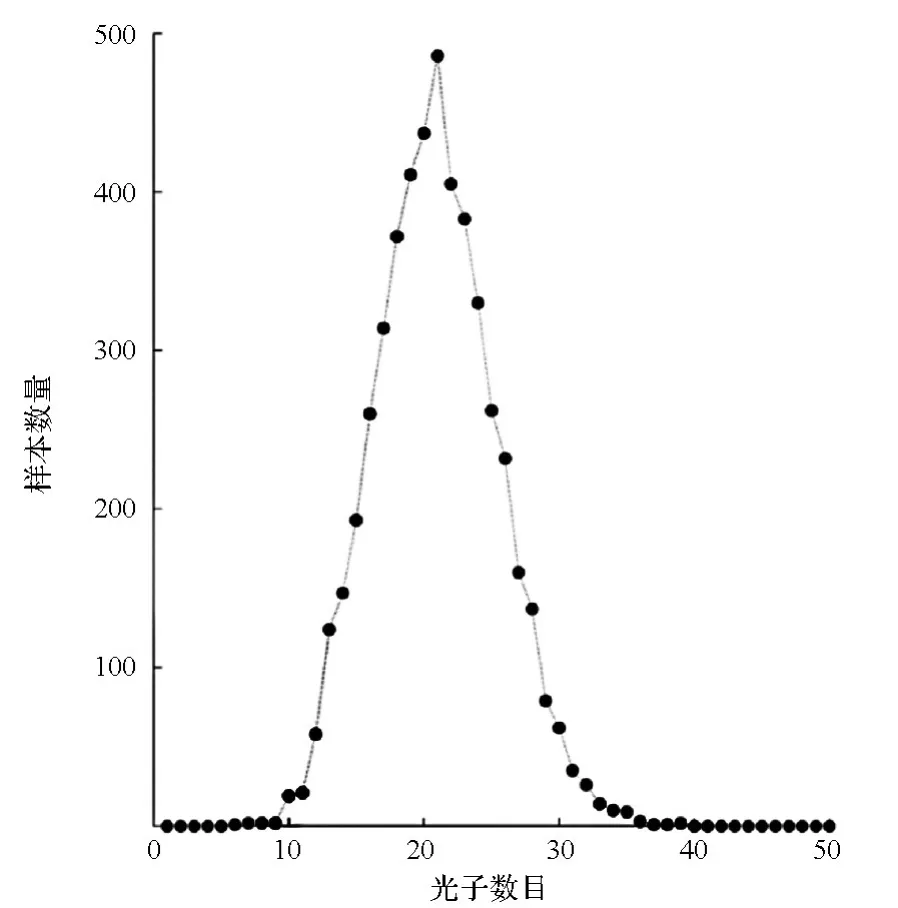
图2 光子数目分布图Fig．2 Distribution of the number of photons

2.3 分段统计

生成250个周期，即10s的观测数据，然后进行历元折叠后，将一个周期均分为8个部分，对每部分的光子数进行χ2拟合优度检验，皮尔逊χ2统计量计算方法与2．1节相同。各段的光子个数期望E(Nts)值计算如表1所示。考虑到pi过小

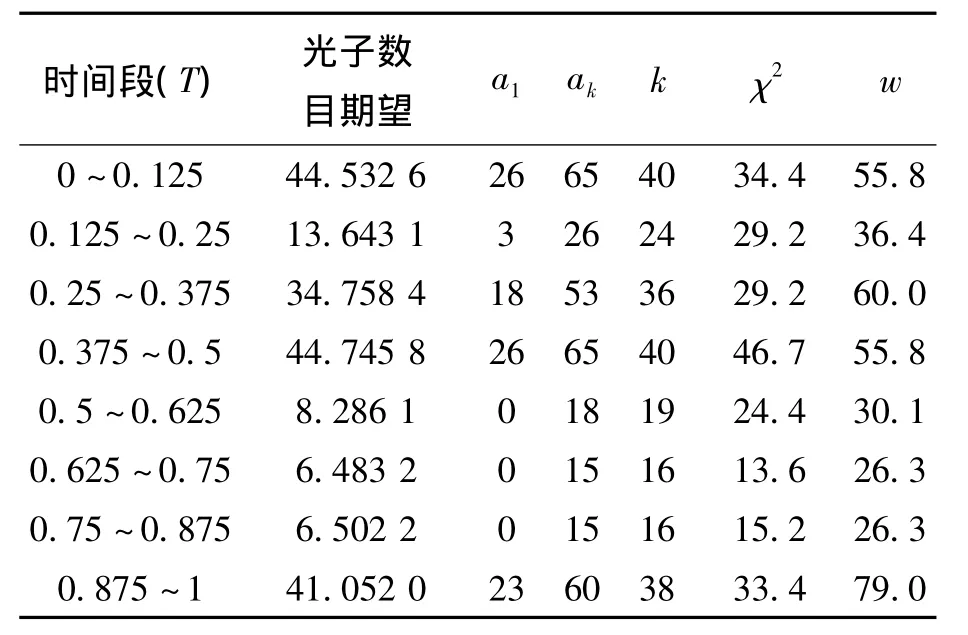
表1 分段统计各段的参数及计算结果Tab．1 Parameters and results of each section for the section-divided method

可能会导致极大的计算误差，因此将p

i

＜10

-3

的光子数目按区间统计，a的取值集合为(［0，a

1

］，

，实验数据及结果如表 1 所示。由表中数据可知每一段的统计量χ

2

均小于

，说明在每一段上产生的光子数目也服从泊松分布。

2.4 信号模拟算法比较

前面介绍了两种信号模拟算法，并提出了一种基于分段线性函数拟合脉冲轮廓函数的模拟算法，将基于光子数分布率的信号模拟算法记为方法一，将采用式(15)由反函数推导的信号模拟算法记为方法二，基于分段线性函数拟合脉冲轮廓函数的模拟算法也利用反函数导出，与方法二的区别在于计算过程不采用近似，将其记为方法三。下面分别比较三种算法生成的光子数期望和由模拟信号构建的观测脉冲轮廓。

2.5 光子数目比较

根据X射线脉冲星的光子流量分布规律，取三组不同的λs和λb，

1)λs=15ph/s，λb=5ph/s

2)λs=150ph/s，λb=50ph/s

3)λs=1500ph/s，λb=500ph/s

表2 光子数目比较Tab．2 Comparison of photon counts

观测时间取100s，统计1000次实验的光子数均值，结果如表2所示，由表可见方法二的光子数目与理论值相差较大，特别是当光子流量较小时尤为明显，而方法一和方法三则趋近于理论值。

2．6 观测脉冲轮廓比较

由于当光子流量较小时，方法二不能有效模拟脉冲信号。故取 λs=1500ph/s，λb=500ph/s，观测时间取100s，历元折叠时间仓取128，构建观测脉冲轮廓。进行1000次实验，统计观测脉冲轮廓每个离散点取值的均方差，并与理论值比较，结果如图3所示。方法二模拟的脉冲信号其轮廓误差最大，其次为方法一，而本文提出的方法三误差趋近于理论值，说明该方法可以重构标准脉冲轮廓。

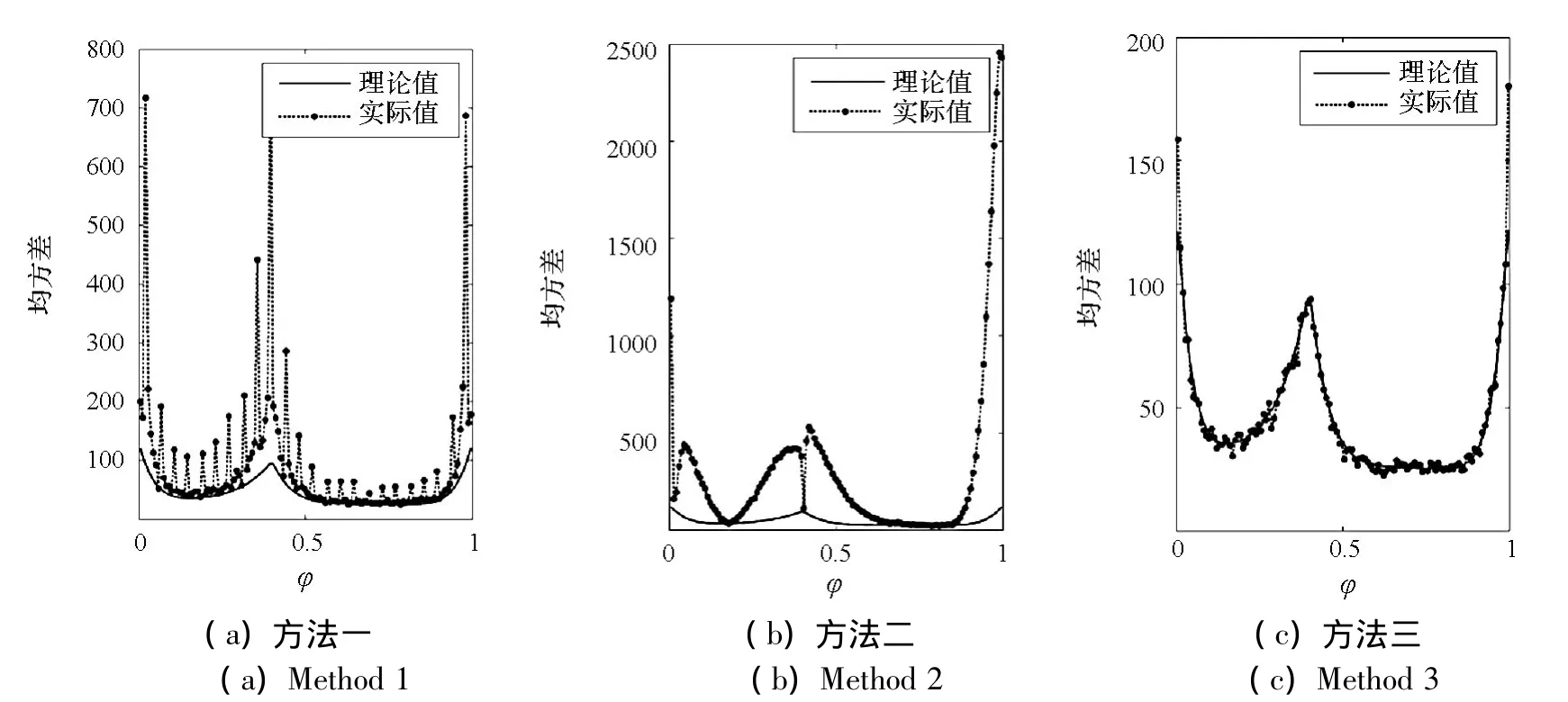
图3 脉冲轮廓误差与理论值的比较Fig．3 Comparison between the error of pulse profile and analysis result

图4 显示的是将模拟产生的 10s，100s，1000s的光子到达时刻通过历元折叠后得到的累积脉冲轮廓，可发现当时间越长时，脉冲轮廓越接近标准脉冲轮廓函数。进一步证明了方法三可以重构的脉冲星信号。

3 结论

本文提出一种基于精确光子流量函数的纯数值重构X射线脉冲星信号的模拟算法，该算法依据X射线脉冲星信号的光子到达数目服从泊松分布性质，用概率论的相关方法模拟光子到达的随机事件，并采用分段线性函数拟合脉冲轮廓解决了轮廓函数积分及其反函数不易求得的问题。该方法不需要借助其他硬件设备即可生成模拟的X射线脉冲星信号，成本低、灵活性高，可以作为X射线脉冲星导航实验的信号源。通过拟合优度检验验证，本算法重构的脉冲星信号服从泊松分布，符合脉冲星信号特征。

图4 累积脉冲轮廓与标准脉冲轮廓的比较Fig．4 Comparison of accumulated pulse profile and standard pulse profile

将提出的新算法与两种已有的算法比较，结果显示新算法在光子数和脉冲轮廓误差上都最接近理论值，说明其最接近实际信号。

通过历元折叠检验新算法表明其有效可行。将三种时间长度的模拟信号进行历元折叠，获得其累积脉冲轮廓，显示当累积时间足够长时，脉冲轮廓趋近于光子流量函数(即标准脉冲轮廓)。表明该算法可有效模拟X射线脉冲星信号，为X射线脉冲星导航的研究提供了信号源基础。

References)

［1］ Hosken R W，Wertz JR．Microcosm autonomous navigation system on-orbitoperation［C］//Proceedings of the Annual AAS Guidance and Control Conference，Keystone，Colorado，1995:491-506．

［2］ 杨博．航天器星敏感器自主定位方法及精度分析［J］．宇航学报，2002，23(3):81-84．YANG Bo．The method of autonomous position determination using star sensor and analysis of precision for spacecraft［J］．Journal of Astronautics，2002，23(3):81-84．

［3］ Counley R，White R，Gai E．Autonomous satellite navigation by stellar refraction［J］．Journal of Guidance，Control，and Dynamics，1984，7(2):129-134．

［4］ Wertz JR．Spacecraft attitude determination and control［M］．Kluwer Academic Publishers，1978．

［5］ Downs G，Reichley P E．Techniques formeasuring arrival times of pulsar signals I:DSN observations from 1968 to 1980［J］．NASA Jet Propulsion Laboratory，California Institute of Technology，Pasadena CA，NASA Technical Reports NASACR-163564，1980．

［6］ 杨廷高，仲崇霞．脉冲星时稳定度及可能应用［J］．时间频率学报，2004，27(2):129-137．YANG Tinggao，ZHONG Chongxia．Frequency stability of pulsar time scale and possible application［J］．Journal of time and frequency，2004，27(2):129-137．

［7］ 桂先洲，黎胜亮，李志豪．基于X射线脉冲星绝对定位中的整周模糊度改进算法研究［J］．国防科技大学学报，2010，32(3):33-36．Gui Xianzhou，Li Shengliang，Li Zhihao．Study of betterment arithmetic of ambiguity in absolution position based on X-ray pulsar［J］． Journal of National University of Defense Technology，2010，32(3):33-36．

［8］ Sheikh S I，Hanson J E．Spacecraft navigation and timing using X-ray pulsar［J］．Navigation，2011，58(2):165-186．

［9］ Emadzadeh A A，Speyer J L．X-ray pulsar-based relative navigation using epoch folding［J］．IEEE Transactions on Aerospace And Electronic Systems，2011，47(4):2317-2328．

［10］ Rinauro S，Colonnese S，Scarano G．Fast near-maximum likelihood phase estimation of X-ray pulsars［J］．Signal Processing，2013，93(1):326-331．

［11］ Sheikh S I．The use of variable celestial X-ray sources for spacecraft navigation［D］．University of Maryland，2005．

［12］ 胡慧君，赵宝升，盛立志，等．基于X射线脉冲星导航的地面模拟系统研究［J］．物理学报，2011，60(2):853-861．Hu Huijun，Zhao Baosheng，Sheng Lizhi，etal．A simulation experiment system for X-ray pulsar based navigation［J］．Acta Physica Sinica，2011，60(2):853-861．

［13］ 孙海峰，谢楷，李小平，等．高稳定度X射线脉冲星信号模拟［J］．物理学报，2013，62(10):109701．Sun Haifeng，Xie Kai，Li Xiaoping，et al．A simulation technique of X-ray pulsar signals with high timing stability［J］．Acta Physica Sinica，2013，62(10):109701．

［14］ 苏哲，许录平，王婷．X射线脉冲星导航半物理仿真实验系统研究［J］．物理学报，2011，60(11):819-826．Su Zhe， Xu Luping， Wang Ting． X-ray pulsar-based navigation semi-physical simulation experiment system［J］．Acta Physica Sinica，2011，60(11):819-826．

［15］ Emadzadeh A A，Speyer J L．On modeling and pulse phase estimation of X-ray pulsars［J］．IEEE Transactions on Signal Processing，2010，58(9):4484-4495．

［16］ 黎胜亮，刘昆，吴锦杰．脉冲轮廓建模仿真与去噪研究［J］．国防科技大学学报，2013，35(4):26-29．Li Shengliang，Liu Kun，Wu Jinjie． On modeling and denoising of X-ray pulsar profile［J］．Journal of National University of Defense Technology，2013，35(4):26-29．

［17］ 徐轩彬，吴鑫基．脉冲星PSR2111+46平均脉冲分析和谱特性［J］．中国科学 A 辑，2002，32(12):1134-1141．Xu Xuanbing， Wu Xing Ji． Spectrum characteristic and analysis ofmean pulse of pulsar PSR2111+46［J］．Science China(A)，2002，32(12):1134-1141．

［18］ Rankin JM．Toward an empirical theory of pulsar emission．IV-Geometry of the core emission region［J］．The Astrophysical Journal，1990，352(3):247-257．