硬式光滑非线性振动系统隔振模型仿真分析

谢 文, 王 慧

(电子科技大学 a.电子工程学院； b.物理电子学院，四川 成都 610000)



硬式光滑非线性振动系统隔振模型仿真分析

谢 文a, 王 慧b

(电子科技大学 a.电子工程学院； b.物理电子学院，四川 成都 610000)

将电磁振动给料机及摩擦摆等工程方面的硬式光滑非线性振动系统引入到汽车的隔振系统中，依据隔振和硬式光滑非线性系统的基本模型，推导计算相关动力学方程，得到受迫振动条件下相应的幅频响应关系式。分析得知，通过减小阻尼比，降低弹簧静形变，并在一定范围内增大非线性恢复力的三次项系数，可明显降低振动幅值，增强隔振效果。同时通过Matlab软件，仿真得到系统的幅频响应特性曲线。对比仿真表明，硬式光滑非线性振动系统的有效设计可提高车辆交通工具的舒适性、稳定性，这样的设计有一定的工程参考价值。

硬式光滑非线性振动系统; 隔振； Matlab； 稳定性

0 引 言

车辆平稳性，舒适性的设计中必须考察隔振系统的特性。隔振系统的隔振特性高低由车辆行驶时系统振幅的变化特性度量。目前的隔振系统主要有单极隔振系统、两级隔振[1]系统、松弛型隔振系统、气垫隔振系统、悬架隔振[2]系统、两级串联型“惯容-弹簧-阻尼”悬架隔振[3]系统、双层隔振系统和悬置系统[5-7]等,大部分系统都将现有频率改为不同的振动频率来阻尼振动的传递，达到隔振目的[8]。目前非线性振动系统或非线性振动特性的应用技术迅猛发展，硬式光滑非线性振动系统，已被用于电磁振动给料机、近共振型振动输送机和共振筛等一系列振动机械中[9]。硬式光滑非线性系统作为车辆隔振系统，可有效降低车辆振幅对车辆负载的敏感性，由此提高车辆行驶的稳定性能，舒适性能。

1 硬式光滑非线性振动系统模型

非线性弹簧作用下的系统动力学方程及所受恢复力[10-13]可表示为：

(1)

(2)

由非线性弹簧与粘性阻尼组成的质量-弹簧系统在简谐力激励下的受迫振动，通常假设其恢复力具有式(2)的三次多项式规律。其振动方程如下：

(3)

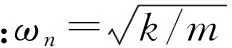
(4)

代入式(3)左边，利用三角函数公式：

可化简为：

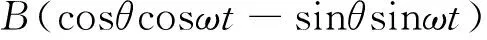
(5)

其中，省略部分为高次谐波，s为引入的量纲一的激励频率比，其大小等于ω/ωn。令上式两边一次谐波的系数相等，可得：

(6)

2ζsA=Bsinθ

从式(6)中消去参变量θ，导出受迫振动的振幅与频率的关系式：

(7)

此非线性系统的振幅与频率的关系式：

借助以上物理模型，我们可以通过Matlab对振动的幅频特性进行仿真分析。

2 模型仿真分析

运用Matlab仿真出幅频响应曲线，选取不同参数B，仿真结果如图2～4所示。

根据仿真曲线易见，当硬式弹簧的三次项系数ε在保证是小量的情况下越大，骨架倾斜越明显，且共振振幅最大值越小；阻尼比相对越大时，振幅随频率比增

图1 非线性系统幅频曲线ε=0.04，B=1

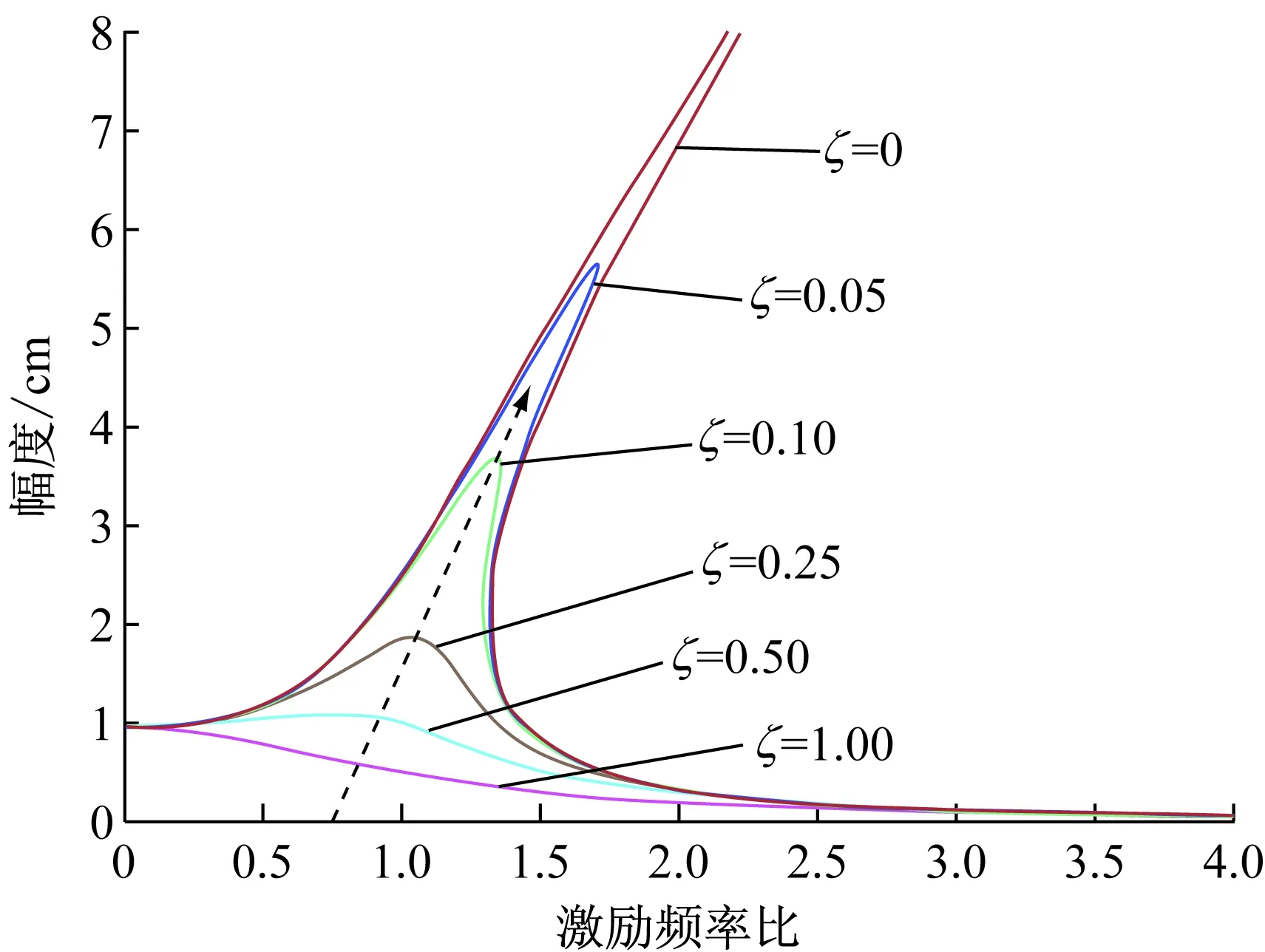
图2 非线性系统幅频曲线ε=0.08，B=1

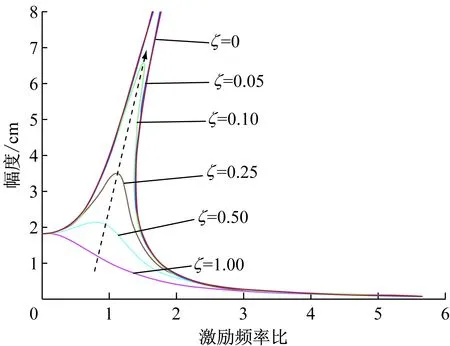
图3 非线性系统幅频曲线ε=0.04，B=2

图4 线性系统幅频曲线ε=0.04，B=1

大变化越小,在亚共振区振幅稳定性明显优于线性振动系统[14-16]。另外，非线性系统的幅频特性曲线并非单值函数。在激励频率的某些区间内，同一频率可对应于3个不同值，易出现振幅滞后现象，而在这三个振幅值随激励频率的改变而改变的过程中，可能发生跳跃现象，这是非线性系统特有的现象[14],如图5所示。

图5 振幅跳跃现象

3 结 语

通过对硬式光滑非线性弹簧隔振系统幅频关系进行推导，借助Matlab仿真出幅频特性曲线，在假设成立的基础上，得出硬式非线性隔振系统能有效地克服振幅不稳定给工作性能带来不良影响这一缺点，提高汽车等交通工具的稳定性，同时给工程设计提供一些参考方向。

[1] 陈 龙.基于二元件ISD结构隔振机理的车辆被动悬架设与能研究[J].振动与冲击,2013(32):90.

[2] 张 雨.汽车悬架隔振性能-混沌特征关系的实验分析[J].实验力学,2005，20(3)：417.

[3] 陈 龙,张孝良.基于半车模型的两级串联型ISD悬架性能分析[J].机械工程学报,2012，4(6):102.

[4] 孙玉华.双层隔振系统模态匹配分析及其振动特性[J].振动．测试与诊断,2014，34(4):728.

[5] 陈 克,吕 品.汽车动力总成悬置系统隔振性能仿真方法[J].中国机械工程,2014，25(20)：2830.

[6] 王晓锋.汽车动力总成悬置系统隔振特性研究[J].中国机械,2014(9):89.

[7] 蒋汪萍.汽车发动机的隔振研究[J].中国教育技术装备,2011(30):86-88.

[8] 赵吉刚，李玉发.悬置隔振原理及其应用[J].农业装备与车辆工程,2010，50(10):6-7.

[9] 闻邦椿,李以农.振动利用工程[M].北京：科学出版社.2005.175-177.

[10] 谢善娟.用Matlab分析非线性弹簧振子的振动[J].赤峰学院学报,2009(4)：7-8.

[11] 王海波.Duffing方程非线性振动特性的计算与分析[EB/OL].西安建筑科技大学,2009.

[12] 顾致平.非线性振动[M].北京：中国电力出版社，2012.

[13] 藤小英.Physics for Scientists and Engineers with Modern Physics(Third Edition)[M].北京：高等教育出版社,2005.

[14] 郑伯兴,周雷靖.汽轮发电机弹簧隔振基础的隔振效率分析[EB/OL].电力建设,2011.

[15] 刘延柱,陈立群.振动力学[M].2版. 北京：高等教育出版社.2011.

[16] 丁文镜.减振理论[M].2版. 北京：清华大学出版社.2014.35-51.

Simulation and Analysis of Hard Smooth Nonlinear Vibration Model in Vibration Isolation System

XIEWena，WANGHuib

(a. School of Electronic Engineering; b. School of Physics and Electronics,University of Electronic Science and Technology of China, Chengdu 610000, China)

Hard smooth nonlinear vibration system which has been used in electromagnetic vibrating feeder and friction pendulum engineering is introduced to the vibration isolation system of cars. From the basic vibration isolation and smooth hard nonlinear vibration model of restoring force, through dynamic formulas, the paper gets the corresponding relation between the amplitude and frequency under the condition of forced vibration. Decreasing the damping ratio, reducing spring static deformation, and increasing three nonlinear restoring force coefficient within a certain range can obviously reduce the vibration amplitude. At the same time, through the simulation software Matlab, we get the exact image of amplitude-frequency characteristic curves. By comparative analysis, it can come to the conclusion that it contributes positively to vehicle comfort and stability. The research has certain reference value to engineering design.

hard smooth nonlinear vibration system; vibration isolation; Matlab; stability

2015-09-09

谢 文(1995-)，男，四川德阳人，在读本科生。

E-mail:locotriangle@hotmail.com

王 慧(1963-)，女，四川成都人，副教授，研究方向为金融物理，双语物理教学。E-mail:kay_wh@163.com

O 328

A

1006-7167(2015)12-0090-02