两类教育测评的碰撞与启示

许世红

国际学生测评项目（The Program for International Student Assessment，简称PISA）是一项面向15岁在校学生的大规模国际性教育评价项目，测评目的是了解在终身学习的背景下，年轻一代在阅读、数学、科学、财经、协作问题解决等领域为成人生活所做的准备情况，并为参与测评的国家调整和制定教育政策提供决策依据。因此，PISA考察的重点是学生在现实生活中运用知识和技能的能力（采用2小时的纸笔测试或计算机测试），以及学生、教师和学校所在的教育系统和教育背景情况（采用问卷调查）。

根据教育部规划，中国部分省市将正式参加PISA2015，有关试测已于2014年4月10-12日在广东、浙江、江苏的75所样本学校举行，试测阅卷编码工作也于同年5月2-11日完成。笔者有幸参加了PISA2015试测的数学阅卷编码工作，深切感受到PISA教育测评与我国基础教育测评的差异，体会到了巨大冲击。

一、关于数学素养及其测评

（一）PISA2015数学素养与测评模型

PISA2015的主测试领域是科学，数学作为副测试领域，沿用PISA2012对数学素养的界定和测评模型。数学素养指的是“在各种各样现实情境中表达、运用和解释数学的个人能力，包括数学推理能力，运用数学概念、规则、定理和工具描述、解释和预测现象的能力；即作为一个积极主动、关心社会、善于思考的现代公民，在现实社会中遇到问题时能够顺利激活其具有的数学知识和数学能力去解决问题，并做出有理有据的数学判断和决策”[1]。因此，PISA对数学素养的测评紧密围绕解决现实生活中的问题来展开。

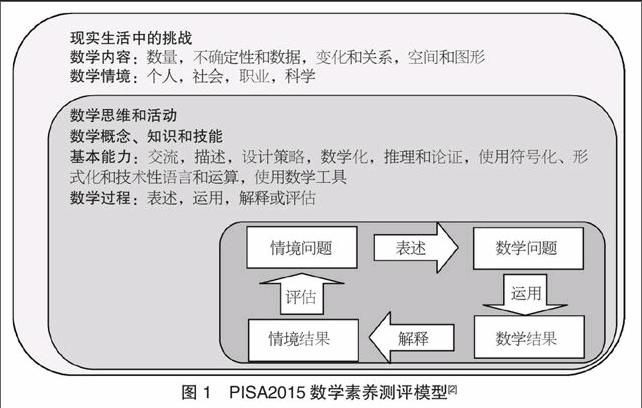
2015年数学素养测评模型表达为三层镶嵌方框（如图1），外层方框展现的是数学素养运用的领域，即解决四类现实情境和四个数学板块中产生的问题与挑战；中层方框体现的是解决问题与挑战需要运用的三个维度的数学思维和活动；内层方框则概要描述了用数学方法解决现实问题的基本流程。

根据数学素养测评模型，PISA2015试测从内容、情境、过程三个维度挑选试题，其中，数学内容四个板块占比为1∶1∶1∶1，四类数学情境占比为1∶1∶1∶1，三个数学过程的占比是表述：运用：解释=1∶2∶1，每个数学过程则从7个基本能力的角度进行描述。试题以单元为主题呈现，且每个单元分属唯一的情景类型，每道试题分属唯一的内容类型和过程类型（由于保密原因，下面选择已解密的PISA试题加以说明）。

【案例1】摇滚音乐会（PISA2003试测解密样题）[3]

摇滚音乐会预留了长100米、宽50米的长方形场地作为观众席。该场音乐会的门票全部售完，而且观众席站满了歌迷。请问：下列哪个数最有可能是出席该场音乐会的人数？

A. 2 000 B. 5 000

C. 20 000 D. 50 000

E. 100 000

分析：本题约28%的考生选择答案C，中等难度。考查的内容板块是数量（尽管也涉及到长方形知识）。问题情境属于社会类。数学过程属于表述（尽管三个数学过程都有所涉及，但主要考查的是把场地大小与形状、音乐会爆满、歌迷站满观众席等信息表述成数学形式，并确定条件中缺少一些信息，但可以根据生活经验提出假设进行估算）。

（二）国内中考数学能力与测评框架

国内初中毕业生学业考试（简称中考）是义务教育阶段的终结性考试，考查目的是全面、准确地反映初中毕业生在学科学习方面所达到的水平[4]。因此，中考数学的考查重点是数学课程标准的达成情况，也期望了解数学课程、数学教学实践、教学管理对学生数学学习的潜在影响。新课程实验以来，中考数学也一直在加强试题与社会实际和学生生活的联系，特别是加强在具体情境中综合运用所学知识分析和解决问题能力的考查，但这类试题数约占试卷总题数的15%左右。另外，各地结合当地使用的教材与教学实际还会出台相应的考试大纲。由于中考命题的主要依据是课程标准和考试大纲，根据《义务教育数学课程标准（2011年版）》，结合考试大纲对试卷结构的说明，数学内容、课程目标、数学能力这三条主线与试卷结构一起构成了各地中考数学的基本测评框架（如表1）。

根据中考数学的基本测评框架和教学课时的分布比例，在中考数学试卷中，数学内容的分布比例约为：数与代数：图形与几何 ∶ 统计与概率=4∶ 4∶ 1，“综合与实践”的考查则分散到前面内容中；四类课程目标的达成情况均有考查，但分布比例难以划分；学生的十种数学能力与意识的掌握与运用水平也均有考查，同样地，分布比例难以划分。虽然各地的试卷结构可能有较大差异，但同一个地区的中考数学试卷结构基本保持多年稳定。

【案例2】分解因式：8（x2-2y2）-x（7x+y）+xy（某市中考试题）

分析：本题满分10分，平均得分7.72分，中等难度，区分度0.64。考查内容属于数与代数板块；考查的知识技能主要包括整式运算和分解因式，需要学生先将代数式化简，然后再运用平方差公式分解因式；考查的数学能力主要是运算能力。

对比PISA数学素养测评模型和中考数学基本测评框架，我们发现，PISA和中考的考查各有侧重：PISA紧密围绕解决现实生活问题这一核心，涉及的数学内容相对浅显，但设计的问题情境丰富多样，并且对如何考查数学思维活动与过程给予了详细的规划，具有较强的可操作性；中考紧密围绕课程标准这一核心，考查的数学内容系统、全面，但涉及现实情境的题目相对单薄，对知识与技能的考查很详细，但如何有效考查数学思考与问题解决的活动与过程，尚停留在经验描述层面。中考测评在情境设计、思维过程考查等方面可以借鉴PISA的成功经验。

二、关于评卷的原则与方法

（一）PISA评卷的计分方法与编码原则

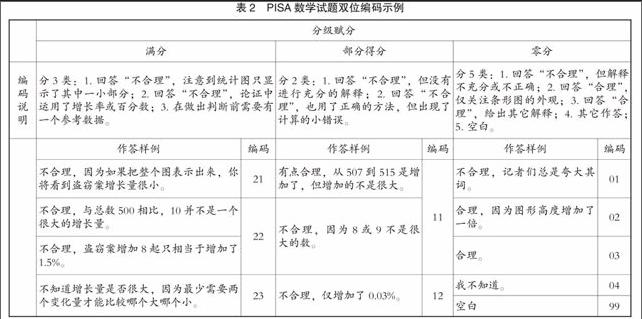
PISA测评的理论基础是项目反应理论，试题难度与考生数学素养的高低建立在同一个量尺上。试题分为选择题、封闭式解答题和开放式解答题三种题型。选择题和大部分封闭式解答题均采用0、1两级计分；少量封闭式解答题和全部的开放式解答题因为答案的多样性和考生能力水平的差异性，需要采用多级计分，阅卷呈现的是0、1、2三级计分。