中国养老金缺口的预测分析——基于滚动机制的灰色预测模型

林雪勤

(安徽师范大学 数学计算机科学学院，安徽 芜湖 241000)



中国养老金缺口的预测分析
——基于滚动机制的灰色预测模型

林雪勤

(安徽师范大学 数学计算机科学学院，安徽 芜湖 241000)

文章针对中国现存的养老金“空账”现象，构建了滚动GM(1,1)模型，研究分析养老金的收支状况，从而为降低养老金的缺口提出相应的对策。

养老金缺口；滚动GM(1,1)模型；预测

近年来，随着我国城镇职工养老保险金制度的基本建立以及退休人员待遇的逐年提高，参保覆盖面日益扩大，养老保险基金规模不断上升，在制度层面上提前完成了城市和农村居民社会保障全覆盖，成为我国社会保障事业发展的重要里程碑。然而,在现行养老保险制度确立之前，企业员工基本无需缴纳养老保险费用，但这部分职工退休后却要从养老保险基金中领取养老金，仅靠统筹账户不足以应对当期发放，加之各地财政实力不同，多数地区不得不采用了“现收现付制”的方法，这使得中国养老保险缴纳与支付同时进行，形成了非常大的养老金缺口。

科学准确地预测中国养老金收入与支出是制定养老金保险制度的重要前提，同时也有利于减轻现存养老金缺口的现状。目前国内常用的预测模型是灰色预测GM(1,1)模型，然而杨淑玲等人通过研究发现，用GM(1,1)模型进行预测时，预测时间越长，模型的精度就越低，不利于中长期的预测。Diyar Akay等人认为可以采用滚动机制，不断更新系统的信息，加强近期数据的影响。因此本文将利用滚动机制与GM(1,1)模型相结合，建立滚动GM(1,1)模型，克服GM(1,1)模型在中长期预测方面的局限性，对于中国养老金缺口给出更为准确的预测，从而为养老金政策的制定给出可靠的实证依据。

1 滚动GM(1,1)模型及检验方法

1.1 滚动GM(1,1)模型的建立

步骤一：对x(0)作一次累加生成和一次均值生成，分别得到累加数列x(1)和z(1)均值数列为：

经计算，可得a和b的值，当a∈(-2,2)时，模型是有效的。

步骤三：将a和b的值代入式(1)，并求解方程，得到白化响应函数为：

(2)

1.2 滚动GM(1,1)模型检验

1.2.1 可行性检验

1.2.2 模型精度检验

(1)残差检验

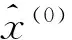
(4)

可得到模型精度为P0=(1-Δ)100%。

(2)后验差检验

计算均方差比值C和小误差概率：

(5)

平均相对误差、均方差比值和小误差概率构成的模型精度检验等级见表1，根据表1确定模型预测精度等级，判定模型是否有效。

表1 精度检验等级参照表

2 养老金缺口预测及分析

2.1 养老金缺口的核算方法

根据我国养老金制度现状的特殊性以及部分地区采用“现收现付制”的方法造成养老金缺口的形成，所以养老金缺口并不是简单地用当年养老金支出减去当年养老金收入，而应该用t年之前养老金总的支出减去t年之前每年的养老金收入与支出之差的和来计算第t年的养老金缺口。据此，给出第t年养老金缺口的计算公式为：

第t年养老金缺口=第t年之前养老金支出总和-第t年之前每年的养老金收入与支出之差的和

表2给出了我国2007年到2011年养老金的收入和支出数据。

表2 2007～2011年我国养老金收入和支出

表2来源于《2011中国养老金发展报告》

2.2 可行性检验

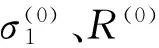
Y(0)=(4772.6,5421.6,10150,12498,16304)，

R(0)=(5668.5,6620.7,8099.4,10142,13064)，

2.3 模型模拟及精度检验

建立5维GM(1,1)基础模型，利用Matlab得到2007年～2011年养老金的模拟结果,如表3所示。

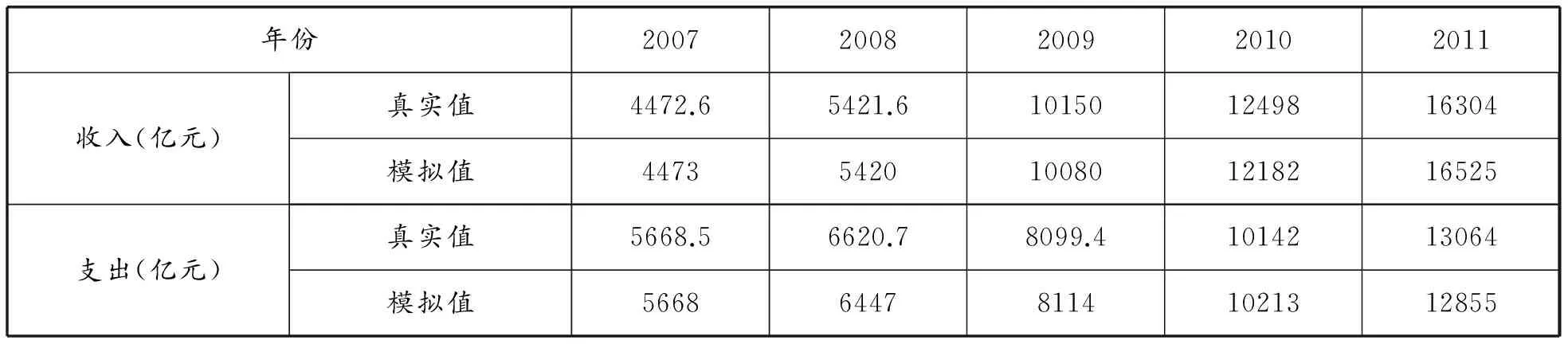
表3 5维GM(1,1)基础模型模拟结果

经计算，得到基础模型精度检验结果见表4。

表4 5维GM(1,1)基础模型精度检验结果

由表4可以看出:养老金收入预测模型的平均相对误差Δ=0.045<0.05，均方差比值C=0.1742<0.35，小误差概率p=1>0.95，模型均通过残差检验和后验差检验，模型精度等级均为二级，并且模型精度达到92.5%；养老金支出预测模型的平均相对误差Δ=0.0102，略大于0.01，模型精度等级为二级以上接近一级，均方差比值C=0.042<0.35，小误差概率p=1>0.95，模型均通过残差检验和后验差检验，模型精度等级均为一级，并且模型精度达到98.98%。

2.4 预测结果及分析

依据滚动GM(1,1)模型，利用Matlab计算得到中国未来二十年的养老金收入和支出，预测结果如图1所示。 由此可见，中国未来二十年的养老金收入和支出都会增加，并且养老金收入增长的速度高于养老金支出增长的速度，但是这并不意味着中国养老金不存在缺口。下面，我们利用养老金缺口计算公式，以2012年为起始年份，将2012年养老金缺口定为0，借助Matlab计算我国养老金缺口的变化，如图2所示。

由图2可以看出：我国养老金缺口显现出先扩大后缩小的变化，其中在2029年时，我国养老金缺口达到最大，缺口金额为2012年养老金缺口再加上2.77×107万元，即在2029年时我国城乡居民养老保险收支矛盾最尖锐。由于中国保险制度的不完善以及养老保险实施过程中的历史遗留问题，造成在养老保险实施的初级阶段，城乡居民养老保险收支矛盾加剧，养老金缺口逐渐增大。另外，随着中国人口老年化的加深，退休人数增加，养老金支出增多。在新农保实施的初级阶段，我国社会保险制度承担的转轨成本较高，政府补贴增多，这些都会导致养老金缺口的扩大。所以在2029年之前，我国的养老金缺口是在增大的。然而，经过十几年的发展，养老保险制度不断完善，经济不断发展，投资理念不断加深以及人口结构的改变都会使养老金缺口缩小，进入良性发展阶段。

3 结论

本文通过对现存养老金缺口现象的研究分析，运用养老金缺口的计算公式核算养老金的收支状况，并构建了滚动GM(1,1)模型对未来30年养老金缺口进行预测，预测出2013年到2035年我国养老金缺口为先增长后减小的变化趋势，并且得出我国城乡居民养老保险收支矛盾最尖锐的时刻是2029年。因此，现有的养老金制度需要进行调整以应对越来越激烈的养老保险收支矛盾，弥补越来越大的养老金“缺口”。具体措施为：第一，靠公共养老金很难养老，国家应加大国有资产划拨社保基金的力度，扩大全国社会保障储备基金；第二，适当延长退休年龄和养老金领取年龄，降低养老金缺口的份额，延缓养老金最高缺口的到来；第三，发展以养老金为主的商业保险，加大商业性养老基金规模，最终形成政府、企业和个人共同组成的养老金制度。

[1] 张思锋，王立刚，张文学.人口年龄结构对基本养老保险基金缺口的影响研究[J].预测，2010(2)：39—41.

[2] 邓聚龙.灰理论基础[M].武汉：华中科技大学出版社，2002：210.

[3] 李恩临.灰色预测方法的应用[J].统计与决策，2010(14)：161—162.

[4] 唐晓云,赵黎明,秦彬.灰色系统理论及其在旅游预测中的应用——以广西桂林为例[J].西安电子科技大学学报(社会科学版)，2007(17)：1—5.

[5] 邹晶，姜志新.基于GM(1,1)的灰色系统模型在我国外贸出口预测中的应用[J].国际贸易问题，2004(2)：27—29

[6] Diyar A, Mehmet A. Grey prediction with rolling mechanism for electricity demand forecasting of Turkey [J].Energy，2007(32)：1670—1675.

[7] Jaw-Yeong Chiang, Chao-Kuang Chen. Application of grey prediction to inverse nonlinear heat conduction problem[J].International Journal of Heat and Mass Transfer，2008(51)：576—585.

[8] 邓聚龙.灰预测与灰决策[M].武汉：华中科技大学出版社，2002：120.

(责任编辑：窦静)

Bases on the existing phenomenon of pension “empty account” in China, this paper mainly researches on the receipts and expenditures of the pension, employs the rolling GM (1, 1) model to predict the amount of pension income and expenditure in China from 2013 to 2035.The results show that the sharpest moment of urban and rural residents endowment insurance payments contradictory come in the year of 2029, finally put forward countermeasures and suggestions for reducing sharp degree of the pension gap.

pension gap ；rolling GM(1,1)；forecast

2015—01—22

安徽省高校省级自然科学基金项目“弱相依过程非线性统计量渐近性理论研究”(KJ2012Z125)；安徽师范大学重大项目“皖江区域产业升级的动力机制与发展路径研究”(FRZD201302)的阶段性成果

林雪勤(1987—)，女，安徽阜阳人，安徽师范大学硕士研究生，主要研究方向：金融数学。

F812.45；F224

A

1672—9536(2015)01—0029—04