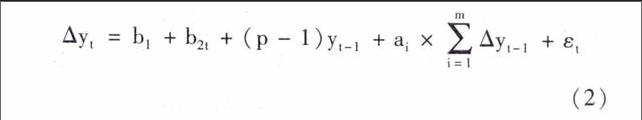中国工资、经济增长、人口与失业之间动态关系研究
蒋文莉+刘日星
摘要:本文通过对工资、经济增长、人口和失业之间时间序列变量的平稳性、协整性和序列相关性检验和经验分析发现:中国失业率与工资变动率之间呈正相关关系;人口自然增长率与失业率呈负相关关系,中国人口自然增长率每上升1个百分点,失业率大约下降1.36个百分点。中国经济增长率与失业率呈负相关关系,经济增长率每上升1个百分点,失业率大约下降0.05个百分点。
关键词:失业率;经济增长率;工资变动率;人口自然增长率
中图分类号:F014.32文献标识码:A
文章编号:1000-176X(2015)03-0120-05
一、问题的提出
失业问题是当前世界各国共同关注的重要宏观经济问题,进入后金融危机时代,随着中国经济增长方式的转变,中国内部需求成为政府政策主要指向对象,也是当前理论研究者所面对的现实问题。一般来看,工资具有刚性或粘性,随着时间的推移,呈现出只增不降的趋势。在中国市场经济改革向纵深推进的背景下,显然,稳定物价、治理失业成为政府必须面对的现实和紧迫问题。经济增长、人口增长也是各国共同关注的经济问题,如果经济高速增长,产出超出潜在产出水平,那么此时的失业率就会小于自然失业率(自然失业率是指充分就业时的失业率);相反,经济萧条时,产出水平小于潜在产出水平时,失业率就会大于自然失业率。人口增长从长期看,会增加未来劳动力人口数量,从而影响劳动力市场供求关系,进而影响工资水平。一般来看,人口适度增长,有利于经济增长,人口衰退或过度增长,一定程度上不利于经济增长,人口结构也是影响经济增长的一个重要因素。当前,中国经济增长处于转型时期,国家在进行宏观经济调控时,既要保持经济增长,又要避免经济过热,这样,失业率及其影响因素如人口、工资和经济增长成为关注热点。那么究竟多高的失业率才适度呢?当前要保持适度的失业率,工资、经济增长和人口增长水平之间的变动关系如何呢?这就是本文所要论述的主要问题。
二、文献回顾、数据来源及说明
1958年,英国经济学家Phillips[1]依据1861—1951年英国的失业率和工资变动率的历史数据,描绘和推导出菲利普斯曲线,表明英国失业率和工资变动呈现出一种负相关关系。然而,1960年,Samuelson等[2]通过修正,以通货膨胀率替代工资变动率,得出通货膨胀率和失业率之间的关系为互补关系。关于经济增长率与失业率之间的关系,一般学者们认为,经济增长是劳动力需求水平上升的主要动因。因为经济增长速度越快,劳动力市场对劳动力的需求量就越大,所以社会的就业岗位增加,提高就业水平,降低失业率;反之亦然。奥肯认为,失业率和国民经济增长率之间呈反方向变化,失业率每高于自然失业率1%,实际国内生产总值便低于潜在国内生产总值2%[3]。关于失业问题的探讨有很多,在分析失业性质和失业原因方面,主要有李培林[4]的 “人口主因理论”,王诚[5]的“制度性失业”论、杨宜勇[6]的“劳动市场分割”理论和项光勤[7]的“结构论”。有关适度失业率的标准,学术界目前没有统一的认识。20世纪60年代一些经济学家认为,一个国家或经济体失业率在4%以下即认为是充分就业的失业率,可是在20世纪80年代中后期之后,又有一些经济学家提出,失业率在5%甚至6%以下就可以认为是充分就业的失业率[8],而任栋等[9]认为中国适度城镇登记失业率的上限为4.2%。以此为依据,本文通过运用1978年中国改革开放以来的工资变动率、失业率和经济增长率数据,以工资变动率、经济增长率和人口自然增长率为自变量,以失业率为因变量进行回归分析,量化分析这四者之间的影响关系。为中国政府制定三者协调的经济可持续发展政策提供理论参考,这对促进中国经济全面、协调、可持续发展,深入推进和谐中国梦建设具有理论和现实意义。
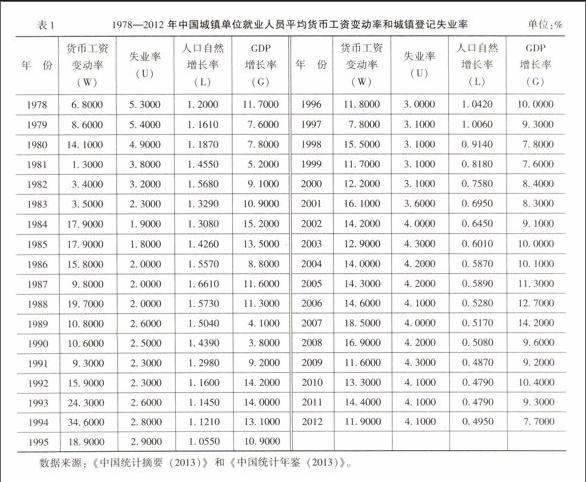
本文使用的数据来源于《中国统计摘要(2013)》[10]和《中国统计年鉴(2013)》[11]。工资变动率指的是1978—2012年中国城镇单位就业人员平均货币工资的变动率,取的是每年对上一年的环比变动比率。失业率是指1978—2012年中国城镇登记失业率。经济增长率、失业率、人口自然增长率和工资变动率都是年度指标。人口自然增长率是指一年内人口自然增长数与年平均总人数之比,用千分率表示,文中的数据把千分率换算成了百分率。1978—2012年中国城镇单位就业人员平均货币工资变动率、经济增长率、人口自然增长率和城镇登记失业率的具体数据如表1所示。
表11978—2012年中国城镇单位就业人员平均货币工资变动率和城镇登记失业率单位:%
年份货币工资变动率(W)失业率(U)人口自然增长率(L)GDP增长率(G)年份货币工资变动率(W)失业率(U)人口自然增长率(L)GDP增长率(G)
19786.80005.3000
三、模型构建及经验分析
根据以上分析,以失业率为因变量,工资变化率、经济增长率和人口自然增长率为自变量,假定其他因素不变,建立因变量和自变量之间相互的关系模型如下:
U=αW+βG+φL+c+μ(1)
其中, W 为工资变动率;U为失业率;G为经济增长率;L为人口自然增长率; α、β和φ为参数,c为常数项, μ为随机干扰项。
1.对1978—2012中国失业率、工资变动率、经济增长率和人口自然增长率数据检验
(1)单位根检验
按照格兰杰检验理论,如果使用非平稳序列进行回归时,那么就会造成虚假回归,另外假如变量存在着单位根非平稳时,对于传统的统计量,像t值、F值、DW值和R将会出现偏差。在研究过程中,为了保证回归结果的无偏性、有效性和最佳性,一般使用扩展的迪基-富勒(Augmented Dickey-Fuller,简称ADF)检验工具去检验样本数据的时间序列特征,关于ADF平稳性检验,可以运用回归方程:
Δyt=b1+b2t+(p-1)yt-1+ai×∑mi=1Δyt-1+εt(2)
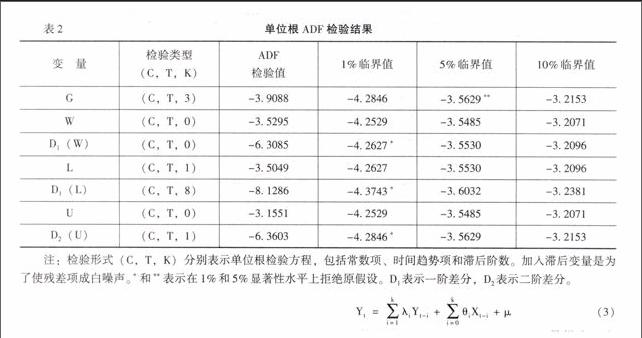
εt为纯粹白噪音误差项,滞后阶数的选择使得εt不存在序列相关。原假设H0 :P=1,备选假设H1 :P<1。接受原假设意味时间序列含有单位根,即序列是非平稳的。利用Eviews6.0先后对变量G、W、L、U的水平值、一阶差分或二阶差分序列进行ADF检验,检验结果如表2所示。
由表2中的数据可知,G的ADF值小于5%显著水平下的临界值,是平稳序列。W 、L和U时间序列的ADF统计量大于5%的显著性水平下的临界值,接受原假设,时间序列含有单位根,是非平稳序列;一阶差分序列D1(W)、D1(L)的ADF值、二阶差分序列D2(U)的ADF值小于1%显著水平下的临界值,是平稳序列。
从表3的检验结果可以看出,按照检验水平5%判断,变量U与G、U与L、U与W之间至少存在一个协整关系。正如格兰杰指出,若变量之间存在协整关系,则这些变量至少存在一个方向的格兰杰因果关系。所以,笔者将进一步探讨上述各组变量之间是否具有统计上引起和被引起的关系,将在后面的回归分析中参照实际经济情况进行分析。
(3)格兰杰因果检验
根据英国经济学家格兰杰检验理论,笔者主要从预测的角度分析变量之间的因果关系,例如格兰杰在考察序列x是否是序列y产生的原因时,一般分为两个步骤:第一步,估计当前的y值被其自身滞后期取值所能解释的程度。第二步,验证通过引入序列x的滞后期取值是否可以提高y的被解释程度。如果是,则称序列x是y的格兰杰原因,此时x的滞后期系数具有统计的显著性。按照格兰杰理论,格兰杰因果关系检验需要从下面两个回归方程进行估计:
Yt=∑ni=1aiXt-i+∑ni=1biYt-i+μ1t(4)
Xt=∑mi=1ciXt-i+∑mi=1diYt-i+μ2t(5)
方程中的白噪声μ1t和μ2t假定是不相关的。可以假定检验的零假设为:
H0:a1=a2=∧=an=0
H0:d1=d2=∧=dm=0
在对这个假设进行检验时,一般可以采用F检验。在拒绝前者而不拒绝后者的情况下,可以判断存在由x到y的单向因果关系,反之不存在;在两个假设都不拒绝的情况下,可以判断x和y是两个独立的序列;在两个假设都拒绝情况下,可以判断x和y之间存在双向因果关系。U与G、U与L、U与W的格兰杰因果检验结果如表4所示。
从表4可以看出,在滞后1阶的情况下,根据1%的显著性水平判断,W是U变动的格兰杰原因;在滞后4阶的情况下,根据1%的显著性水平判断,G、L是U变动的格兰杰原因。
2.对1978—2012年中国失业率、工资变动率、经济增长率和人口自然增长率数据回归分析
运用Eviews6.0软件,根据表1数据,以失业率为因变量,工资变化率、经济增长率和人口自然增长率为自变量,建立失业率随着工资动率、经济增长率和人口自然增长率变化的回归方程:
U=0.0435W-1.6965L-0.0447G+6.0925(6)
(-1.7470)(-5.1440)(-0.8190) (9.8780)
R2=0.4900 DW=0.3400
在拟合的结果中,方程的拟合优度较低,仅为0.4900,且变量的显著程度也较低,因而原方程无法通过检验。由此可以看出,这个模型在解释中国的失业率与工资变动率、经济增长率、人口自然增长率关系中表现不明显,它无法准确解释中国的失业率与工资变化率、经济增长率、人口自然增长率之间的关系。因此,再对此模型进行LM检验,在5%显著性水平下,此模型存在1阶序列相关性和3阶序列相关性。通过一阶自回归AR(1)模型和三阶自回归模型AR(3)进行修正,拟合后的回归方程结果如下:
U=0.0015W-1.3129L-0.0532G+4.9796+
(0.2010) (-4.1200 ) (-3.1600) (12.4380)
0.9470AR(1)-0.2534AR(3)(7)
(7.3860) (-2.9820)
R2=0.9400 DW=2.1200
对修正后模型进行LM检验,模型在5%显著性水平下不存在序列相关性,且检验结果不能拒绝原假设,检验结果如表5所示。
表5Breusch-Godfrey系列相关性LM检验
F值
0.1697
概率F(2,24)
0.8450
观察R2
0.4461
概率χ2(2)
0.8001
因此,通过一阶自回归AR(1)模型和三阶自回归模型AR(3)修正后的回归方程的估计结果是有效的。另外,方程回归结果中,看单个自变量T检验结果发现,自变量L、G在1%水平拒绝原假设,通过检验;但是自变量W在84.2300%水平接受原假设,不能通过检验,所以修正后的回归方程要剔除自变量W的影响,因而方程不能显著有效地反映变量W 和U 之间的关系,只能有效反映变量L、G 和U 之间的关系。根据1978—2012年经济数据,除去变量W 后重新回归得到方程:
U=5.0349-1.3593L-0.0522G+0.9285AR(1)-
(13.8900) (-4.6450) (-3.2760)(7.7100)
0.2472AR(3)(8)
(-2.9840)
R2=0.9400 DW=2.1300
以上方程表明:
第一,就单个工资变动率来说,工资变动率与失业率系数为0.0010,正向变动关系得不到检验。
第二,通过实证回归分析,我们发现中国人口自然增长率与失业率呈负相关关系,修正后回归相关系数为-1.3593,说明中国人口自然增长率每上升1个百分点,失业率大约下降1.36个百分点。
第三, 通过实证回归分析,我们发现中国经济增长率与失业率呈负相关关系,修正后回归方程中相关系数为-0.0522,这说明中国经济增长率每上升1个百分点,失业率大约下降0.0500个百分点。
四、结论
本文通过对1978—2012年中国失业率、工资变动率、经济增长率和人口自然增长率数列的平稳性、协整性和序列相关性进行检验,建立工资变动率、经济增长率、人口自然增长率数与失业率关系模型,分析中国经济增长率、人口自然增长率对失业率影响关系的有效性,揭示了经济增长率、人口自然增长率和失业率间的数量关系,实证结果表明:中国失业率接近充分就业失业率,经济增长速度属于适当水平。在进行经济宏观调控时,以2012年城镇居民登记失业率4.1000%为参照,在其他因素不变的条件下,为了使城镇居民登记失业率不超过4.2000%的水平,当前的经济增长率下降幅度不能超过两个百分点。同理,在其他因素不变的条件下,为了使城镇居民登记失业率不超过4.2000%的水平,人口增长率下降幅度最多不能多于0.0740百分点。另外,中国的工资变动率与失业率呈正相关关系不显著。
参考文献:
[1]Phillips,A.W.The Relationship between Unemployment and the Rate of Changing of Money Wages in the United Kingdom,1861—1957[J]. Econometric,1958,25(7):283-299.
[2]程永波,范恺峰,陈洪转,等.江苏失业与物价水平权衡关系的实证研究[J].华东经济管理,2014,(1):8-14.
[3]高鸿业.西方经济学(宏观部分)[M].北京:中国人民大学出版社,2004.607.
[4]李培林.中国就业面临的挑战和选择[J].中国人口科学,2000,(5):1-8.
[5]王诚.中国就业发展新论——核心就业与非核心就业理论分析[J].经济研究,2002,(12):79-92.
[6]杨宜勇.中国转轨时期的就业问题[M].北京:中国劳动社会保障出版社,2002.174-175.
[7]项光勤.解决结构性失业是当前我国劳动就业中的关键问题[J].江海学刊,2007,(6):14-21.
[8]伍荣.对改革与完善失业保险制度的思考 [J].经济体制改革,1997,(4):103-106.
[9]任栋,李萍,孙亚超.中国失业率水平的适度调控目标区间研究[J].经济学家,2014,(2):28-35.
[10]国家统计局.中国统计摘要(2013)[M].北京:中国统计出版社,2013.
[11]国家统计局.中国统计年鉴(2013)[M].北京:中国统计出版社,2013.
(责任编辑:巴红静)