某小型风机提高风能利用率的研究

李鹿野，张维竞

(上海交通大学 海洋工程国家重点实验室，上海 200240)

分布式电网是未来的新能源发展趋势，小型发电设备可以满足用户照明、电器使用等最基本的生活需要，在使用清洁能源的同时有效降低大型电站输送过程中所造成的电能损失。分布式电网常见的利用形式有风能、太阳能和生物能等。本文研究的对象是小型风力发电机。

Savonius 小型垂直式风机于1931 年由芬兰工程师Savonius 提出，其具有能够在低风速下起动，不受风向限制和结构承载能力强的特点［1］。典型结构由两个半圆形叶片构成，断面呈“S”型(如图1 所示)。国内外的学者采用风洞试验和数值模拟的方法对该型风机进行了探究。风动试验研究了叶片数目［2］、高径比(d/h)［3］以及叶片重叠比(e/d)［3］等参数对风机性能的影响，得出了各项的最优区间;计算机仿真了得到叶片周围流体的速度矢量分布以及叶片表面各处的压力分布情况［4－5］。

尽管对于该型风机的研究已经取得了较大的进展，但是该型风机的固有缺点依然存在，Savonius 风力机的整体风能利用率较其他风机偏低。因此，需要对该型风机进行进一步的改进，以规避上述问题。Burcin Deda Altan、Kunio Irabu 等人［6－8］提出了应用导流板来增加风机风能利用率的方法，但是并没有对导流板的各因素对风机风能利用率的影响进行更为深入的探讨。本文通过数值仿真方法讨论了导流板的各因素对该型风机风能利用率的影响及其合理使用的可能，为该型风机的设计提供有益的参考。

1 基本方程与计算方法

本文研究的风机尺寸如图1 所示，叶片圆弧直径d=0．5 m，叶片重叠比e/d =0．1，叶片高度h =1 m。

图1 Savonius 型风机外型

式中 u——流体速度;

u'——脉动瞬时值;x——流体位移;p——流体压力;ρ——流体密度;μ——流体动力粘度;S——源。湍流模型采用标准k－ε 模型

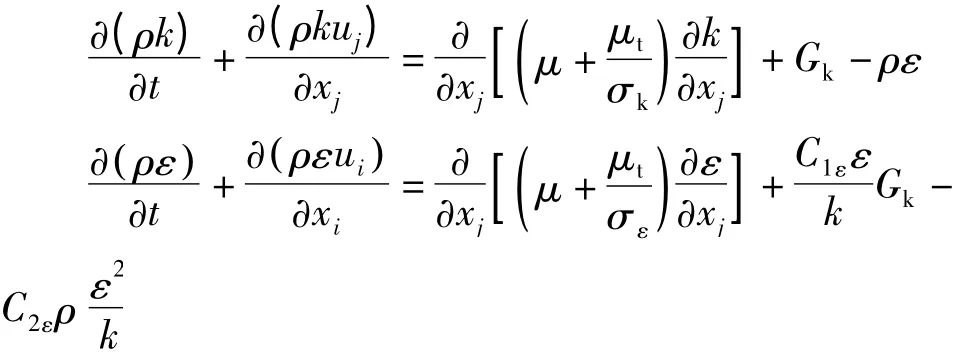
式中

ε——湍流耗散率;

Gk——由平均速度梯度引起的湍动能k 的产生项;

C1ε=1．44，C2ε=1．92。

2 叶片建模与验证

首先建立二维模型，如图2 所示，其中Vw表示来流速度，θ 表示叶片位置。针对上文所述的风机尺寸利用Gambit 建立几何结构以及生成网格。叶片材质为2 mm 厚的钢板，计算域为20 m×40 m 的矩形区域，叶片中心距离入口距离10 m。采用混合方法划分网格，即结构化网格和非结构化网格相结合，网格处理如图3 所示，其中，叶片周围局部加密，边界层首层高度1 mm，共5 层。圆形区域为结构化网格，用Interface 与外部非结构化网格隔开，网格总数为1．7 ×104。

图2 二维示意图

图3 Gambit 网格处理

应用Fluent 作为流动模拟计算的求解器，在二维模型中，左侧为速度入口，上下为壁面，右侧为压力出口，Vw=14 m/s，时间属性为定常流动。在此设定下进行网格无关性验证，计算θ =45°时不同网格密度下叶片对转轴产生的静态力矩，结果如表1。

表1 网格无关性验证

可以看出网格数为1．7 ×104可满足计算精度，同时降低计算量，本文研究中统一采用这种网格密度。

在二维模型的基础上建立三维模型，建模过程中应用叶片沿转轴方向的对称性，将一半的风机置于20 m×40 m×1 m 的计算域中。叶片网格分布如图4 所示，网格数量为1．04 ×106。势上相吻合，且误差都在10%以内，该数值模型能够为之后的数值计算提供较为可靠的计算基础。基于这一事实，本文的研究均采用二维模型。

图4 三维叶片示意图

3 模拟计算结果及分析

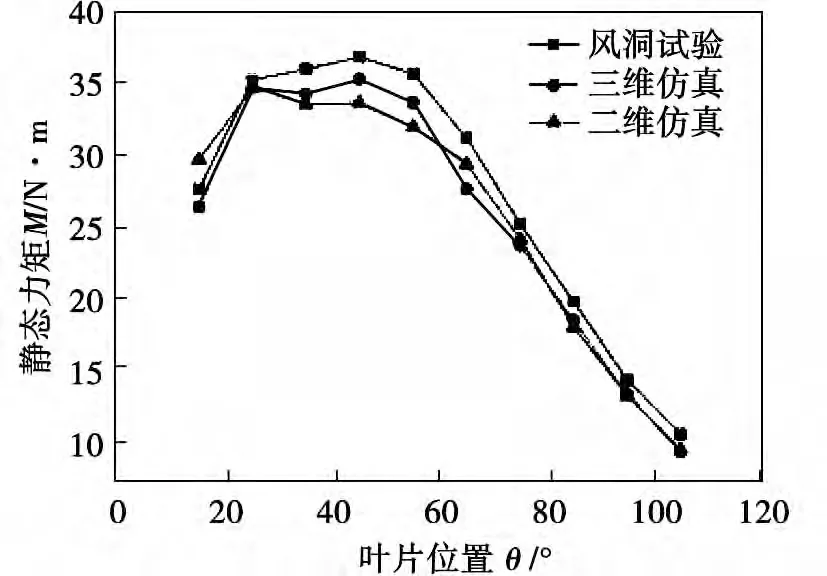
图5 二维、三维仿真与风洞试验结果对比

Robert 等人对此风机进行了风洞试验［10］，在确定来流方向条件下，叶片每隔10°转动一次，通过叶片与来流方向相对角度的变化来模拟不同的来流方向以及叶片转动到不同位置时的风机表现。风洞试验测量了θ 在特定位置下叶片相对于转动轴所产生的力矩大小。本文采用上述实验研究的实验数据作为本文数值模型的校正基础。叶片转动以180°为一个周期，从风动试验和本文的数值计算结果可以看出，叶片在15° ～105°之间输出力矩较大［11］，而在其余范围内输出力矩较小，因此本文重点讨论在该角度范围内的试验和计算结果。二维、三维仿真与风洞试验结果对比如图5 所示，通过图5 可以看出，二维、三维数值仿真均与风动试验的结果在整体趋

本文在来流方向增加导流板，以提高风机效率，安装导流板的风机俯视图如图6 所示，网格细节处理如图7 所示。

图6 导流板示意图

图7 加入导流板后网格处理图

本文主要讨论的导流板影响对风机风能利用率的影响因素有导流板与来流方向的夹角α，导流板长度L 以及导流板距叶片转动区域的距离x。

数值计算首先讨论导流板与来流方向的夹角α对叶片力矩的影响，其中设定导流板长度L =1 m，导流板距叶片转动区域的距离为x=0．025 m。当α分别为30°、45°、60°时，风机叶片产生力矩的变化如图8 所示。计算中选取力矩较大的三个位置，即θ分别为35°、45°和55°的情况作为对比分析。通过图8 可以看出，增加导流板后，风机静态力矩明显提高，导流板与来流方向的夹角α=60°时效果最为明显，静态扭转力矩提高幅度为20% ～30%;α =30°情况下静态扭转力矩提高了10% ～20%;α =45°时，提高幅度为15% ～30%。α =45°，θ =45°位置处的速度云图如图9 所示。

图8 导流板与来流角度α 对风机力矩的影响

图9 加入导流板后速度云图

讨论导流板长度L 对叶片力矩的影响，固定导流板与来流方向的夹角为α =60°且导流板距叶片转动区域的距离为x =0．025 m，研究导流板长度L分别为0．6 m、1 m 与1．4 m 时叶片静态扭转力矩的变化。图10 的数值计算结果可以看出，当导流板长度L=0．6 m 时，静态扭转力矩平均提高25%左右，而当导流板长度L =1． 4 时，这一数值可以达到30% ～40%。因此可以看出导流板越长带来的静态扭转力矩提高就越明显。但是随着导流板长度的增加会导致更高的制造成本和安全隐患，因此在实际应用中，应控制导流板长度在合理的范围内。在今后的研究中，需要对导流板长度的合理范围进行更加深入的探索。

图10 导流板长度L 对风机力矩的影响

图11 导流板位置x 对风机力矩的影响

讨论导流板距叶片转动区域的距离x 对叶片静态力矩的影响，取导流板长度L =1 m，导流板与来流方向的夹角α=60°，x 分别为0．025 m、0．01 m 与0．04 m。通过图11 中的实验结果可以发现，导流板距叶片转动区域的距离x =0．04 m 时，在叶片处于θ=35°位置时静态扭转力矩改善明显优于其他两种工况，然而当叶片处于θ =55°位置时静态扭转力矩改善效果与其他两种工况相当。说明导流板与叶片之间较大的距离并不一定提供更高的静态力矩。对比几种情况发现，对应不同的导流板位置x，叶片静态扭转力矩均提高了20% ～30%左右，不同的导流板位置对叶片静态扭转力矩的提升的差异并不明显，体现出了有限的影响作用，因此在实际工程中可以根据制造难度、安装难度以及安全距离对导流板位置作灵活调整。

4 结语

通过本文的仿真结果可以看出，增加导流板能够显著提高Savonius 型风机的静态力矩，进而提高了风机的风能利用率。通过设置不同的导流板长度、角度以及安装位置，讨论了不同导流板因素对提升该型风机叶片静态扭转力矩的影响。导流板能够在有限增加制造成本的基础上对风机性能进行较为合理的改善，有效地弥补了Savonius 型风机风能利用率不高的缺陷。导流板对其他种类的风机叶片静态力矩的影响值得进一步研究。本文主要研究了导流板的三个主要参数，后续研究需要对其他参数如导流板曲度，对叶片的遮挡面积等对力矩的影响进行更全面的分析，也可以对如何调控导流板与来风方向角度进行深入探讨。

［1］田文强，李岩，冯放，等．Savonius 风力机力矩特性的数值计算与风洞试验研究［J］． 可再生能源，2013，31(2):15 －18，23．

［2］Sivasegaram S． Design parameters affecting the performance of resistance－type，vertical－axis windrotors－An experimental investigation［J］．Wind engineering，1977(1):207 －217．

［3］Khan M H．Model and prototype performance characteristics of Savonius rotor windmill［J］． Wind Engineering，1978(2):75 －85．

［4］王军，仁飘零，王兴双． 一种新型垂直轴风力机的CFD 分析［J］．工程热物理学报，2012，33(1):63 －66．

［5］位晓清，王东兴，蔡国忠，等．小型Savonius 风机的创新设计与仿真分析［J］．能源与节能，2012(10):1 －3．

［6］Burcin Deda Altan，Mehmet Atilgan．The use of a curtain design to increase the performance level of a Savonius wind rotors［J］．Renewable Energy，2010(35):821 －829．

［7］Kunio Irabu，Jitendro Nath Roy． Characteristics of wind power on Savonius rotor using a guide－box tunnel［J］．Experimental Thermal and Fluid Science，2007(32):580 －586．

［8］仁飘零，王兴双，王军． 一种新型垂直轴风力机的CFD 研究［C］．武汉:“两区”同建与科学发展第四届学术年会论文集，2010．

［9］Rollet－Miet P，Laurence D，Ferziger J．LES and RANS of turbulent flow in tube bundles［J］． International Journal of Heat and Fluid Flow，1999，20(3):241 －254．

［10］Robert E． Sheldahl，Bennie F． Blackwell，Louis V．Feltz． Wind Tunnel Performance Data for Two － and Three －Bucket Savonius Rotors［J］． Journal of Energy，1978，2(3):160 －164．

［11］位晓清，王东兴，蔡国忠．叶片转角对小型Savonius风机气动性能的影响［J］．电力与能源，2012(4):354 －356．