基于SVD矩阵分解技术和RkNN算法的协同过滤推荐算法

刘 洋

(信阳职业技术学院 数学与计算机科学学院，信阳 464000)



基于SVD矩阵分解技术和RkNN算法的协同过滤推荐算法

刘 洋

(信阳职业技术学院 数学与计算机科学学院，信阳 464000)

针对现有协同过滤算法具有的可扩展性较低、数据稀疏和计算量较大缺点，提出一种基于SVD矩阵分解技术和RkNN算法的协同过滤推荐算法.本算法经SVD矩阵简化处理和kNN和RkNN的协作过滤，增强了用户的影响集，实现了测试集的未知预测评分功能.经仿真实验表明，稀疏性、可扩展性和计算量都得到有效改善，系统预测评分与用户实际评分接近，为用户提供了良好的使用体验.该算法获得了更好的预测性能，同时具有良好的可扩展性.

SVD影响集；协作过滤；推荐算法；RkNN 影响集

0 前 言

在科技日益发达的今天，计算机网络已经覆盖于社会的每一个角落.以百度、搜狗为代表的搜索引擎开始出现在我国人民的视野之中，为中国人的日常生活和工作带来了极大的便利.现阶段我国搜索引擎具有个性化的特点，其推荐的系统多为基于用户推荐、基于项目推荐、基于内容推荐，上述的这些协同过滤算法具有数据稀疏、可扩展性差和用户相似性难分辨的特点，对推荐系统的质量产生负面影响.随着科学技术的发展，越来越多的专家学者开始关注到推荐系统领域，针对传统算法所存在的问题也做出了针对性改善，其中可扩展性差和系统数据稀疏的问题可通过矩阵分解方式来改善，例如PCA(主成分分析)、NMF(非负矩阵分解)、SVN(奇异值分解)等算法，都可用于降低数据的稀疏性和维度.

1 协同过滤算法基础

解决资源和用户的关系是推荐系统中的主要内容，这里用m×n表示用户与资源之间的关系，其中m代表用户，n代表项目，用户i对项目j的评分用Ri,j表示，则得到下式：

(1)

传统的协同过滤算法主要通过寻求目标用户的最近领导实现，在寻求到若干个领导后获取各个目标项目的评分，进而实现系统推荐.此类推荐方式是以用户兴趣资源为基础的，可有效寻求到受用户喜爱的网络资源，但由于算法的局限性，导致其扩展性和稀疏性较差.其中稀疏性主要是指系统在未获得足够评价的时候，难以根据评价搜寻出符合要求的用户.可扩展性是指在资源和用户不断增加的情况下，系统性能和质量越来越低.目标用户可系统项目的评分可用下式表示：

(2)

在公式2中，用户用u表示，项目由j表示，Rm,j代表用户m对项目j的评分；sim(u,m) 用于表示用户u与数值m之间的相似度.

2 基于SVD矩阵分解技术的用户过滤推荐算法的优化

从目前我国常用的搜索引擎技术来看，系统的稀疏性和可扩展性问题的解决亟不可待.本文基于推荐系统的稀疏性和扩展性，以影响集概念为出发点，通过RkNN、kNN、SVD等计算机技术，提出了一种以用户过滤为基础的推荐算法，勇于推荐系统质量的提高.

2.1 SVD矩阵简化

SVD(奇异值分解)又叫单值分解，是一种基于网络资源的矩阵分解技术，以m×n的矩阵R为例，SVD可将矩阵R变换为3个矩阵，分解过程如图1所示.

图1 SVD矩阵变换

由图可知，A=TSD，在A中，各行都对应了相应的用户，而各列则对应了相应的项目.运用SVD对关联矩阵A进行分解处理，则可得到下式：

R0=T0S0D0,S0=diag(α1,…,αr) (3)

在公式3中，r×n与m×r的正交矩阵分别用D0、T0表示，矩阵R0的秩为r，r×r的对角矩阵用S0表示，α1≥…≥αr≥0被称为单值.

算法1如下：

输入：矩阵R0

输出：相关矩阵T，S，D

(1)采用SVD对R0进行分解处理，得到T1，S1，D1；

(2)简化处理S1，用0替代对角线上所有<1的值，删除全为0的列或行，由此得到S，表示维数为s的对角矩阵；

(3)根据S的简化处理，对T1，D1进行同等处理，得到简化后的T、D，则有矩阵R=TSD，此时R≈R0.

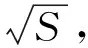
经过对R0的单值分解，使其数据稀疏性得到大幅度的降低，由此可得出较为精准的top-N推荐集和最近邻居集.

2.2 基于kNN和RkNN的协作过滤推荐算法

在对矩阵进行简化处理后，相似用户之间的精准性得到了有效解决.但在系统相似用户缺乏的情况下，简化矩阵后相似用户量更为减少.本文为更好的解决此类问题，特意引入RkNN和kNN技术，使用户影响集得以增强.

逆k最近邻是指在设定的数据集S中，某点被周边点视为最近邻，这里特定点q为周边点的最近邻，从p点周围选取影响最大的点，采用RkNN(kNN算法的逆算法)算法来进行计算.

假设数据集为S，p和q两点之间的距离用D(p，q)表示，则得到RkNN计算公式：

RkNN(q)={q∈kNN(p)|p∈S} (4)

算法2如下：

输入：用A(m，n)表示用户项目评分矩阵，其中i为用户，j为项目；

输出：用户i对项目j上的预测评分；

(1)计算A(m，n)中用户i与周边相关用户之间的相似度，将所得结果存入距离矩阵D；

(2)从距离矩阵D中根据用户i的位置，寻求i点的最近邻序列，获得最近邻列表kNN；

(3)对距离矩阵D进行扫描处理，寻求到用户i的逆最近邻序列，获得逆最近邻列表RkNN；

(4)提取kNN和RkNN列表中的前k个项；

(5)运用公式(2)和公式(5)计算得出用户i对项目j的预测评分，得出p，评分预测公式见下式：

(5)

2.3 基于SVD影响集的协作过滤推荐算法

经过矩阵简化处理可以精确的得到相似用户，而kNN和RkNN算法可有效增加用户之间的影响集，现在SVD矩阵简化和扩大kNN或RkNN影响集的基础上，对相似用户问题和矩阵稀疏性进行改善处理.

算法3如下：

输入：用户和项目评分矩阵R(m，n)与用户i；

输出：用户i接收到的推荐项目序列；

(1)采用算法1中的单值分解方法处理矩阵R，可得到简化后的T，S，D；

(3)计算A(m,k)中用户之间相似度，将所得结果存入距离矩阵中；

(4)针对于用户i，寻求到i点的kNN和RkNN值，保存处理；

(5)寻找用户i在列表kNN中所对应的行，按照从上往下的顺序分别取出前k个项，也就是{i1,i2,i3}，并取出RkNN中对应的k个项；

(6)选择适量参数，分别计算出用户i在项目j上的预测评分，求解出与用户相关的项目推荐序列.

3 实验仿真

采用计算机硬件系统PC作为实验平台，配置为内存2 G，CPU 2.8 GHz，Pentium Extreme，Windows XP.

为更好的验证基于SVD矩阵分解技术和RkNN算法的协同过滤推荐算法在实际运用过程中的效果，本文采用了仿真实验和结果分析.召回率和准确率是衡量网络搜索引擎中的重要指标，这里采用召回率和准确率来检验推荐质量.

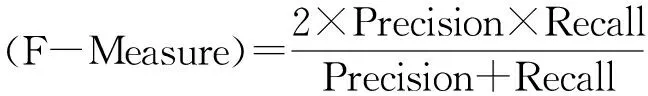
3.1 实验步骤

①首先处理基础矩阵，使得每列的平均值与列中为0的项等同，然后得到经处理后的初始矩阵，在对用户资源矩阵进行SVD技术处理.②将处理得到的用户矩阵和项目矩阵采用kNN，RkNN技术计算预算项目评分，获得综合推荐集.③选择原始用户资源矩阵中浏览次数相对较少的项目，然后得到确定的推荐集.④将参数k值确定后，求解出不同值情况下推荐的平均MAE.

3.2 实验结果

本文实验数为10万条评价记录，则10万条评价记录来自于4500个用户对电影的评价.将10万份数据平均分为10组，每组数据为4500个用户对电影的1万条评价的原始数据.

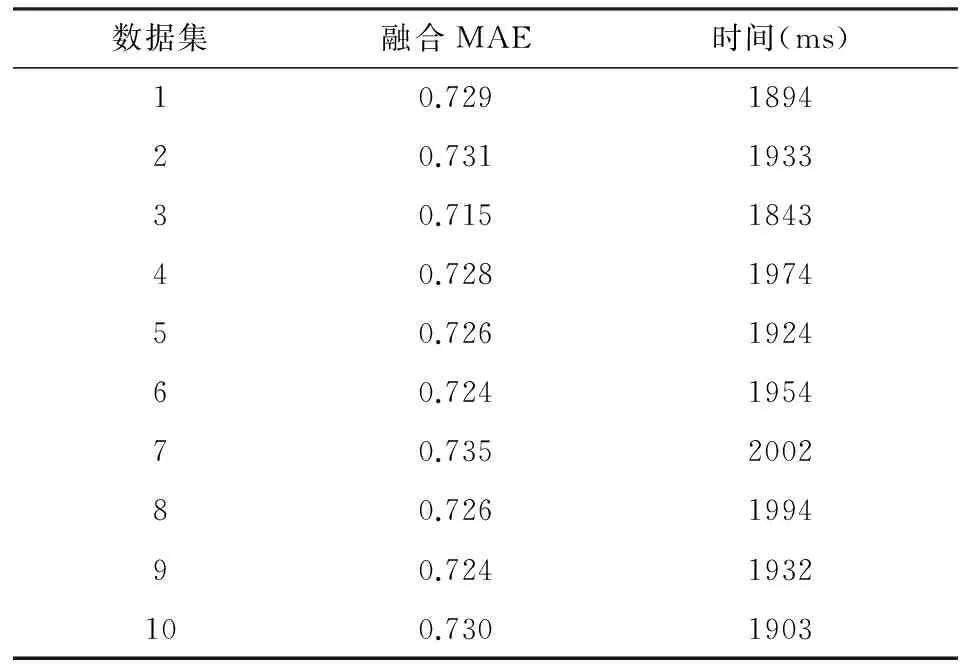
表1 每组数据所消耗的时间

由表1中可知，用户在发出请求到实现推荐的时间大约为2000 ms左右，用户的等待时间较短，易于用户接受.当出现大量数据同时运算时，系统在同时完成大型数据时服务时间也相差较小，用户不论在何种情况下的等待时间均为2000 ms左右.由于系统的时间计算可分为离线和在线两个部分，其中在线推荐的复杂度为O(N*L)，在O(N*L)中，N代表新项目数，L代表协同过滤推荐集数，N与L均为常数，因此O(N*L)属于常数级别，最终可知在线推荐的服务时间与数据量无显著关联，不受数据量变化的影响.上表中可知，数据的变化并不会影响到系统服务时间，所有系统的服务时间均在2000 ms左右.仿真实验证明，系统推荐经SVD技术处理后，稀疏性、可扩展性和计算量都得到有效改善，系统预测评分与用户实际评分接近，为用户提供了良好的使用体验.

[1] 陈彩云,李治国.一种基于SVD和Rough集的信息过滤方法[J].计算机工程与应用,2003,39(34):99-101.

[2] 徐 翔,王煦法.基于SVD的协同过滤算法的欺诈攻击行为分析[J].计算机工程与应用,2009,45(20):92-95.

[3] 王 伟,杨 宁,李丽华,刘国强.基于SVD的K-means聚类协同过滤算法[J].微计算机信息,2012(8):139-141.

[4] 方耀宁,郭云飞,扈红超,兰巨龙.一种基于Sigmoid函数的改进协同过滤推荐算法[J].计算机应用研究,2013,30(6):1688-1691.

[5] XU Jing-ke,SUN Huan-liang,LIU Tian-bo,YU Ge.Location Algorithm Based on RKNN and Its Applications[J].Application Research of Computers,2014,31(3):789-791.

[6] LIU Jin-ling,YANG Feng-xia,LIU Guo-xiang.RkNN of a Group of Object are Queried in the Application of Spatial Database[J].Microelectronics & Computer,2012,29(1):18-22.

Research on Collaborative Filtering Recommendation Algorithm Based on SVD Matrix Decomposition Technique and RkNN Algorithm

LIU Yang

(College of Mathematics and Computer science,Xinyang Vocational and Technical College,Xinyang 464000,China)

Existing collaborative filtering algorithm has the disadvantage of low scalability, data sparsity and large amount of calculation.This paper proposes a collaborative filtering recommendation algorithm based on SVD matrix decomposition technique and RkNN algorithm. Collaborative filtering algorithm and simplifies the processing and kNN and RkNN through the SVD matrix. The algorithm enhances the user influence set and realizes the test set prediction score functionunknown. Simulation experiments show that sparse, cocoa extension and the calculation are effectively improved,system prediction score and actual score are closer to the user.It provides good experience for the user. This algorithm can get better prediction performance and has good scalability.

SVD effect set; collaborative filtering;recommendation algorithm; RkNN effect set

2014-10-20

刘 洋(1975-)，男，硕士，讲师，研究方向：高等数学、计算数学.

TP18

A

1671-119X(2015)01-0044-04