机会式电磁矢量传感器阵列互耦校正算法*

马丽梅，李国岫，赵力行

(1.北京交通大学 机械与电子控制工程学院，北京100044;2.北京自动化技术研究院，北京100009)

0 引 言

传感器阵列中的电磁波极化资源对系统性能的影响超过信号幅度、倾角相位、发射频率和极化波形等因素，因此，深入分析和研究极化资源可进一步优化无线网络通信等性能。而且，电磁矢量传感器构成的传感器阵列已经广泛应用于雷达、无线通信、水下声纳和医学等领域［1，2］。但是，传统的静态式电磁矢量传感器阵列具有明显的互耦效应，导致系统的波达方向和信道质量等性能严重下降［3，4］，成为电磁矢量传感器阵列硬件平台研发和应用的瓶颈问题。因此，研究电磁矢量传感器阵列中的互耦校正算法成为分布式电磁矢量传感器阵列系统应用热点之一。

文献［5］在共形天线阵列中分析载体曲率与方向图指向之间的关系，提出了三维共形天线导向矢量的数学模型。文献［6］研究了均匀线阵互耦矩阵的对称带状特性，提出了适用于互耦未知条件的双基地多输入多输出(multiple input multiple output，MIMO)雷达发射与接收阵列的互耦校正算法。文献［7］采用海洋回波方法校正分布式高频地波雷达阵列的幅相误差，从而解决了雷达系统的阵列互耦误差校正问题。文献［8］将全波数值分析和微波网络理论应用于非理想馈电端口共形阵，建立了共形阵完备互耦校正算法。

针对电磁矢量传感器阵列的互耦校正问题，本文提出了一种基于分布式电磁矢量传感器机会式阵列互耦校正算法。实验结果表明:该算法不仅有效提高了波达方向估计精度，而且具有高空间谱估计精度与信噪比。

1 分布式电磁矢量传感器阵列性能分析

电磁矢量传感器阵列中，假设一个阵元中以远点O 出发有三个电偶极子记为:Tx，Ty和Tz。它们分别沿x，y，z 轴三维拓展，如图1 所示。Tx与Ty的间距为βxy，同理，Tx与Tz的间距为βxz，Ty与Tz的间距为βyz。Tx延x 轴拓展时夹角弧度为ωx，同理，Ty延y 轴拓展时夹角弧度为ωy，Tz延z 轴拓展时夹角弧度为ωz。磁环Hx，Hy和Hz围绕远点O延圆弧成形且分布在x，y，z 轴三个独立区域内。

如图1 所示的电磁矢量传感器的流形矢量通过传统的共点式阵元结构属性结合波动因子得到，如式(1)所示

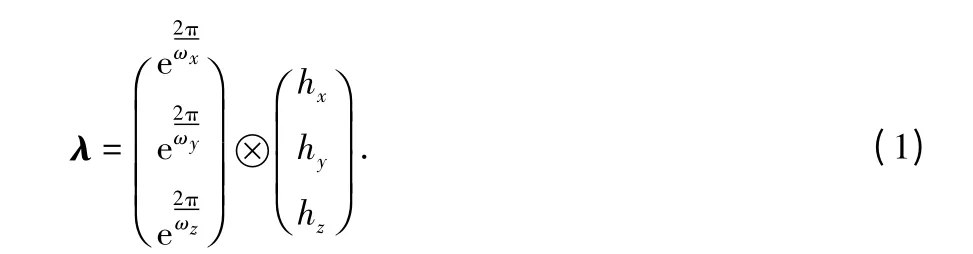
其中，hx，hy，hz分别为传统的共点式阵元结构中磁环Hx，Hy，Hz围绕远点O 线性成形后的位置坐标。

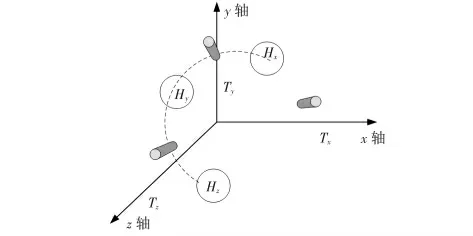
图1 电磁矢量传感器阵元结构Fig 1 Element structure of electromagnetic vector sensor

假设线性阵列、三角形阵列和双三角形阵列分别记为Larray，Tarray，DTarray，电磁矢量传感器接收信号强度为

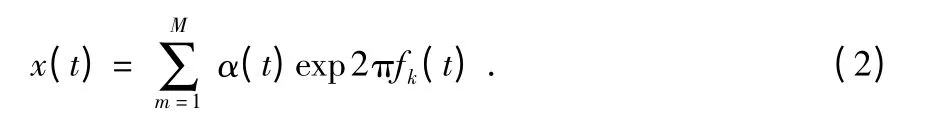
其中，α(t)为阵列种传感器的发射信号强度，fk(t)表示信号传递过程中发射功率。

基于式(1)和式(2)，结合图1 所示的阵元结构，电磁矢量传感器阵列的信噪比、波达方向估计精度和孔径扩展维数感知分析，如式(3)、式(4)和式(5)所示

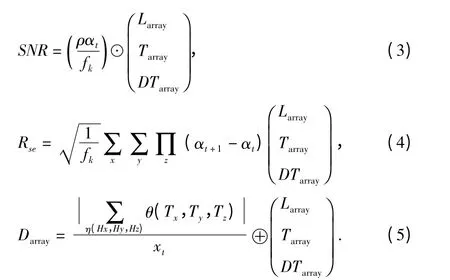
图2 给出了线性阵列、三角形阵列和双三角形阵列三种不同传感器阵列的信噪比、波达方向估计精度和孔径扩展维数的变化规律。从图2(a)中看出:俯仰角较小时线性阵列和三角形阵列因阵元较少，信噪比明显低于双三角形阵列，然而，当弧度增大到一定程度时，信噪比开始优于双三角形阵列，这是因为双三角形阵列的复杂度太大导致性能下降。从图2(b)中发现，双三角形阵列的波达方向估计精度在信噪比较低时明显高于线性阵列和三角形阵列，然后，当信噪比足够大即高于40 dB 后，三角形阵列的波达方向估计精度逐步接近双三角形阵列，且三角形阵列的复杂度要小于双三角形阵列。双三角形阵列的孔径扩展维数在信噪比4 dB 时发生抖动，前后性能发生逆转，线性阵列和三角形阵列的孔径扩展维数随着信噪比的增大线性增大。

图2 参数感知分析Fig 2 Analysis on parameters sensing

2 机会式互耦校正算法

从上文中三种传感器阵列的信噪比、波达方向估计精度和孔径扩展维数的性能分析发现，分布式电磁矢量传感器阵列可以根据实际传感器属性、工作状态和阵列性能，机会式动态调整阵列结构，从而优化性能，校正互耦。

对任意几何结构的电磁矢量传感器阵列，按照如图3所示的三维坐标轴划分区域，在不同区域内按照线性阵列、三角形阵列和双三角形阵列三种不同传感器阵列几何结构进行布局，机会式传感器阵列的阵元结构属性结合波动因子后如式(6)所示

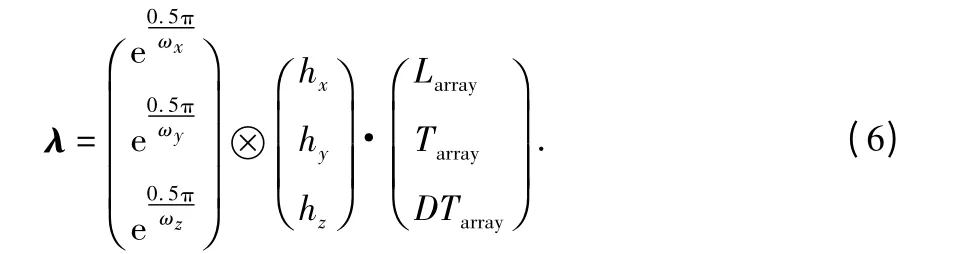
电磁矢量传感器接收信号强度如式(7)所示

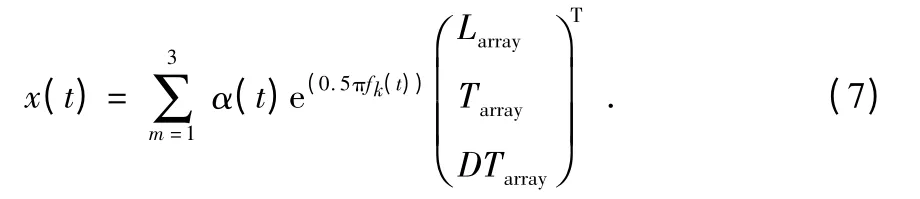
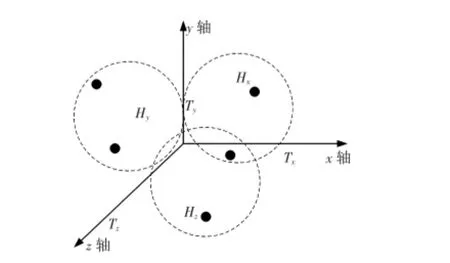
图3 机会式传感器阵列Fig 3 Opportunistic type sensor array

电磁矢量传感器机会式阵列中阵元布设方案、区域划分依据和几何结构成形方法，可能会加剧互耦效应，降低阵列流形清晰度，降低互耦校正效果。因此，根据信噪比、波达方向估计精度和孔径扩展维数等性能按照一定概率选取阵元的区域、几何形状和位置，从而提出了一种基于机会式结构的分布式电磁矢量传感器阵列互耦校正算法，过程描述如下:

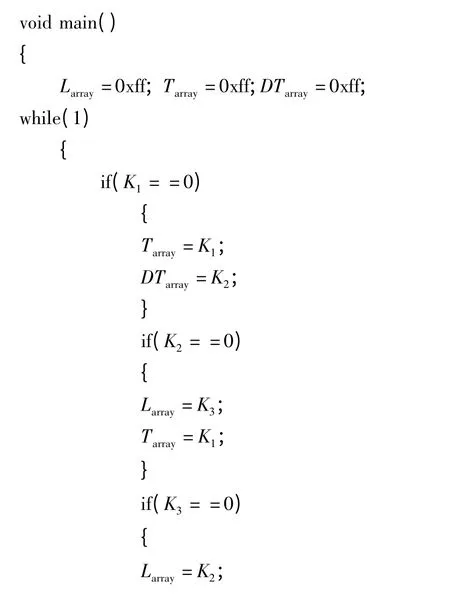
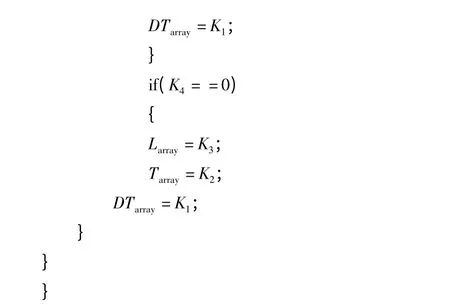
3 算法性能验证

为了验证所提出的电磁矢量传感器机会式阵列的互耦校正算法性能，通过实验与静态电磁矢量传感器阵列的波达方向估计精度、空间谱估计和互耦系数等方面性能进行比对分析。其中，对于互耦系数分析通过5 次实验获得估计平均值。分别在不同俯仰角、信噪比和互耦系数条件下，10 次实验统计阵列性能，统计实验结果如图4、图5 和图6所示，实验参数设置如表1 所示。

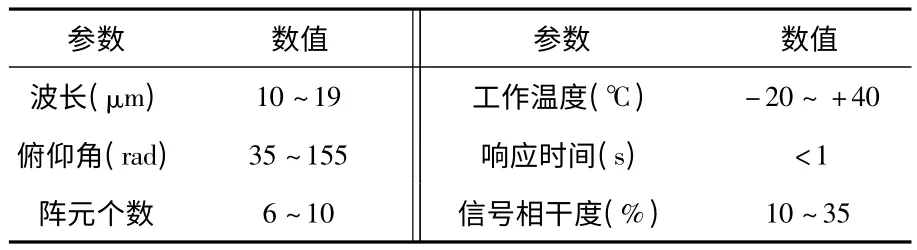
表1 实验参数设置Tab 1 Parameter setting of experiment

图4 给出了所提机会式阵列方案与静态方案在波达方向估计精度方面的性能对比。从中发现，静态传感器阵列方案因几何结构固定，随着俯仰角的弧度增大，波达方向估计精度明显低于所提机会式阵列方案，这是因为所提方案可以很好地融合传感器的动态属性变化和阵列性能变化，机会式布局合理阵列结构。图5 从空间谱估计角度阐述了两种互耦校正算法的性能。从中看出所提互耦校正算法的空间谱估计精度随着信噪比的增大在提高，而静态传感器阵列的空间谱估计精度在不断降低。统计信噪比随着互耦系数的变化结果如图6 所示。其中，静态传感器阵列的统计信噪比对互耦系数不太敏感，只是发生部分抖动，其余情况平稳;而所提机会式传感器真理互耦校正算法随着互耦系数的增大，在统计信噪比上具有明显改善。

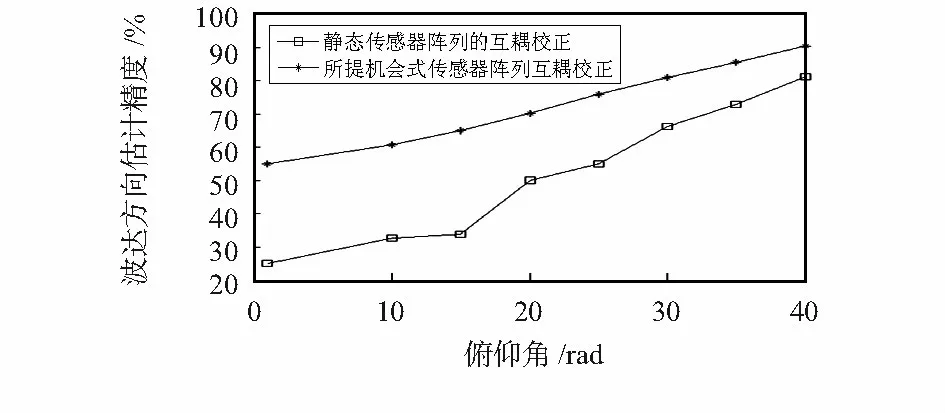
图4 波达方向估计精度Fig 4 Direction of arrival estimation precision

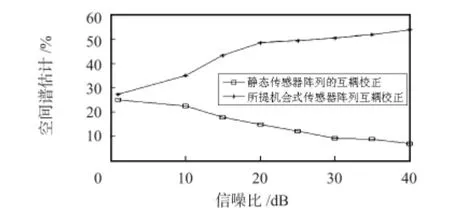
图5 空间谱估计Fig 5 Spatial spectrum estimation

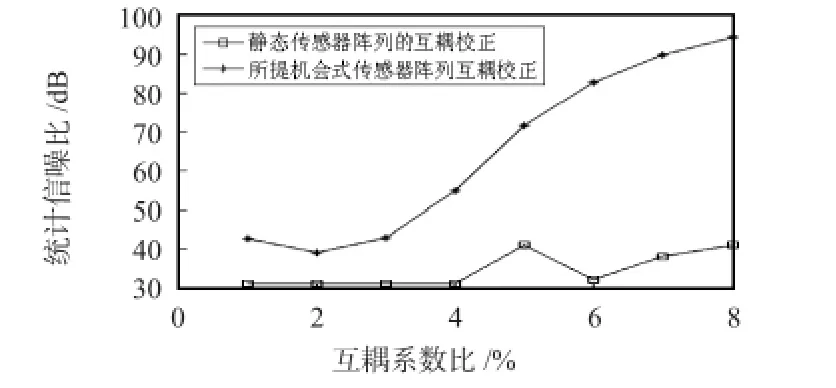
图6 统计信噪比与互耦系数Fig 6 Statistical signal to noise ratio and mutual coupling coefficient

4 结束语

为了弱化和消除互耦效应电磁矢量传感器阵列的性能影响，本文研究了一种分布式电磁矢量传感器机会式阵列互耦校正算法。首先根据线性阵列、三角形阵列和双三角形阵列等阵列的结构特性和性能，建立了信噪比、波达方向估计精度和孔径扩展维数等性能分析模型，并基于上述三方面性能的变化规律构建了电磁矢量传感器机会式阵列架构，最后提出了机会式互耦校正算法及其校正流程。实验结果表明:相比静态传感器阵列，所提分布式电磁矢量传感器机会式阵列互耦校正算法，不仅有效提高了波达方向估计精度，而且具有高空间谱估计精度和信噪比。

［1］ 林 敏，龚铮权.基于子空间的阵元间互祸校正方法［J］.电子学报，2001，29(9):1176－1178.

［2］ Lin Min，Yang Luxi.Blind calibration and DOA estimation with uniform circular arrays in the presence of mutual coupling［J］.IEEE Antennas and Wireless Propagation Letters，2006，5(1):315－318.

［3］ Sellone F，Serra A.A novel online mutual coupling compensation algorithm for uniform and linear arrays［J］.IEEE Transactions on Signal Processing，2007，55(2):560－573.

［4］ 郭利强，朱守平，陈伯孝，等.双/多基地综合脉冲孔径地波雷达的互耦校正［J］.电波科学学报，2008，23(1):134－140.

［5］ 王布宏，侯青松，郭 英，等.共形阵列天线互耦校正的辅助阵元法［J］.电子学报，2009，36(6):1283－1288.

［6］ 刘志国，廖桂生.双基地MIMO 雷达互耦校正［J］.电波科学学报，2010，25(4):663－667.

［7］ 龙 超，吴雄斌，柯亨玉，等.高频地波雷达的阵列互耦校正［J］.华中科技大学学报:自然科学版，2012，40(9):1－5.

［8］ 赵 菲，王生水，柴舜连，等.非理想馈电端口下的共形阵完备互耦分析与校正［J］.电子与信息学报，2013，35(6):1490－1495.