基于MTF的光电成像系统建模仿真

张发强，张玉发，邓 强，程正东，朱 斌

(1.脉冲功率激光技术国家重点实验室，电子工程学院，安徽 合肥230037;2.电子工程学院基础部，安徽 合肥230037)

1 引言

建立合理准确的模型，是光电成像系统研究的一个重要方面，可以为光电成像系统的研制和评价提供理论依据和参考，具有重要的研究价值。光电成像系统建模是一种数学模型的构建，需要综合考虑目标和背景特性、光电成像系统性能、大气环境及多种其他因素。目前光电成像系统建模所采用的方法主要有以下四种:调制传递函数法、光线追迹法、点扩散函数法和基于图像像素处理法［1］。

以上几种建模方法各有优缺点，相对于其他几种建模方法，调制传递函数法把光电成像系统中的光学系统、探测器、信号处理电路和显示装置等组成部分有机地结合起来，使模型具有普遍适用性，同时又可以将各个部分分开，独立地对光电成像系统各组成部分进行分析，具有开放、灵活的特点，该方法深入物理过程，囊括了大多数物理现象，所建立的模型能够较准确地描述真实系统。

本文以调制传递函数为理论依据，分别计算了光电成像系统各组成部分的调制传递函数，求得了系统总的调制传递函数，建立了基于MTF的光电成像系统模型。

2 调制传递函数的理论基础

在利用MTF建模过程中，假设光电成像系统是线性、空间不变系统［2］。调制传递函数是光学传递函数(OTF)的模，描述的是系统对输入各种频率图像的对比度传递能力，表征系统的频率通过量，图1说明了调制传递函数的物理意义。

图1 调制传递函数示意图

从图1可以看出，物体的对比度经过光电成像系统后变小，图像变得模糊，不同的空间频率对应的对比度变化曲线就是调制传递函数。

由信号处理理论可知，MTF是光电成像系统点扩展函数(psf)在频域的傅里叶变换，以二维图像为例，利用psf和MTF表示光电成像系统的输入和输出之间的关系:

式中，x，y为空间坐标;νx，νy为空间频率;式(1)和式(2)分别表示了输出图像与输入图像在空域及频域上的关系。可以看出，通过调制传递函数可以将空域上的卷积转化为频域上的乘积，简化了运算。

3 光电成像系统建模分析

如果一个系统是分立的，并且是线性平行不变(LSI)的，则整个系统的调制传递函数是各个部分调制传递函数的乘积。

根据以上的思想，光电成像系统可以作为LSI系统进行研究，求出各个组成部分的MTF，系统总的MTF为各个组成部分MTF的乘积，将系统总的MTF与输入的图像的傅里叶变换相乘，最后再做反傅里叶变换，并叠加合理的噪声，即可得到系统输出图像，这就是建立基于MTF的光电成像系统模型的核心思想。

所以在利用调制传递函数对光电成像系统进行建模之前，首先要分析光电成像系统的组成部分，并计算各部分的调制传递函数，通常光电成像系统包含以下几个组成部分:目标和背景、大气传输、光学系统、探测器、信号处理电路、显示装置，其模型如图2所示。

图2 光电成像系统MTF模型

从图2可以看出，光电成像系统的输出图像和输入图像之间的关系如下:

式中，σ(x，y)为叠加的噪声，所以求出光电成像系统总的MTF是建模的关键问题，下面对光电成像系统各组成部分的MTF进行分析。

3.1 大气的MTF

大气对光电成像系统的影响主要来源于大气分子散射、气体吸收以及气溶胶散射和吸收三个部分对目标图像传输的影响，吸收和散射引起到达传感器上的光能量减少，而散射和湍流会引起图像的模糊和细节损失。根据大气对光传输的不同影响，将大气调制传递函数分为湍流MTF和气溶胶MTF［3－4］。其中湍流MTF又被分为长曝光时间MTF和短曝光时间MTF，其表达式分别为:

式中，C2n为大气折射率常数，通常采用经验模型计算;r为光传输的路径长度;λ为波长;μ在用于近场时取1，用于远场时取0.5;D为光学系统的入瞳直径，当曝光时间t〈〈10 ms时，认为其满足短曝光条件［5］。

大气的气溶胶MTF分为低空间频率MTF和高空间频率MTF，其表达式如下［3］:

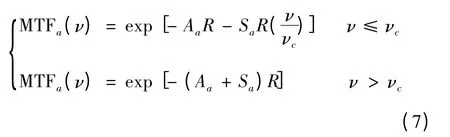
式中，νc是近似为a/λ的截止频率;a是微粒半径;Aa是大气的吸收系数;Sa是大气散射系数;从上式可以看出，大气的高空间频率MTF其实就是透过率，只有在低空间频率时MTF才是空间频率的函数。

通过上面的分析可以看出，光在大气中传输时，会受到气溶胶微粒的吸收和散射，以及湍流的影响，在工程计算中，假设气溶胶微粒对辐射光传输的影响和湍流对光传输的影响是独立的，根据MTF的特点，大气总的MTF为湍流MTF与气溶胶MTF的乘积:

上式即为光电成像系统建模中大气部分的调制传递函数表达式。

3.2 光学系统的MTF

光学系统是光电成像系统的重要组成部分，接收来自景物的光辐射，并把景物图像投射到系统的探测器阵列上。

在实际分析光学系统的MTF时，应该分析引起光学系统成像质量变化的因素。不同的因素对应不同的MTF，光学系统的调制传递函数包括衍射极限的调制传递函数MTFdif和像差产生的调制传递函数MTFabe两部分组成［6］。

Gaskill给出了圆形孔径的光学系统衍射限MTF:

式中，νc=D/λ是光学系统的截止频率，单位为c/mrad;D是光瞳直径，只有当空间频率小于截止频率时，上式才成立，当空间频率大于截止频率时，MTF为零。

由像差引起的弥散斑能量分布近似为高斯函数，具有圆对称形式，其传递函数为:

式中，σ=σc/f是角度度量的标准方差，单位为c/mrad;f为光学系统的焦距。σ与弥散斑所占能量的百分比有直接的关系，假定所有的能量集中在弥散斑内，则标准方差σc取弥散斑直径1/4。

则光学系统总的MTF为:

3.3 探测器的MTF

探测器是光电成像系统的核心部件，它既完成视场内图像的扫描取样，同时通过光电效应将辐射信号转化成电信号。探测器对输入光信号的作用主要有三种:采样、传输和扩散，探测器总的调制传递函数等于这三种调制传递函数的乘积。探测器种类众多，这里以常用的凝视型CCD探测器为例进行分析。

这里只给1－D探测器阵列的具体推导情况，2－D阵列的推导是完全相似的，设其部分尺寸为a，采样间隔d，根据采样定律和探测器的规格可以得出探测器的采样MTF［3］:

从上式可以看出，探测器的采样要同时受到感光区尺寸a和采样间隔d的影响。

CCD在进行信号采样的同时，将光信号转换成电信号并在像元之间转移传输，在传输过程中由于各种原因，必然存在损耗，由此而导致的MTF称之为传输MTF。

设CCD像元的数目为n，像元间的电荷转移损失率为ε，CCD的耐奎斯特频率为νN，则CCD的传输调制传递函数为［7］:

从上式可以看出，nε越大，MTFt就下降的越厉害，所以为了提高CCD的传输MTF，减少电荷转移损失率是至关重要的。

CCD中的光信号在进行传输时，其产生的电荷会扩散到相邻的像元，引起MTF的下降，由于扩散产生的MTF为［8］:

式中，α为材料对光的吸收系数;d为表面耗尽区宽度;L0为光生电荷扩散长度;L是与空间频率有关的量:

从上面两式可知，随着空间频率的增加，MTFd(ν)的值下降。

通过上面的分析，可得探测器总的调制传递函数为:

上式即为光电成像系统建模中探测器部分的调制传递函数。

3.4 信号处理电路的MTF

信号处理电路是光电成像系统的重要组成部分，不同的光电成像系统有不同的信号处理电路，但都可以看作是各种滤波器的集合，在这里主要讨论高通和低通滤波器的调制传递函数。在讨论信号处理电路的MTF的时候，特别要注意电路所传递的是时域信号，其对应的传递函数是时间频率域，所以在实际的应用中要将其转换成空间频率域，这样才能和整个光电系统的MTF统一，其MTF表示如下［9］:

式中，MTFe1(ν)为低通滤波器的调制传递函数;MTFe2(ν)为高通滤波器的调制传递函数;νt0为滤波器的3dB频率;νt0=1/2πRC;R和C为滤波器的电阻和电容;ν0为νt0对应的空间频率;ω为扫描角频率，对不同的成像体制，ω有不同的表示方式。

整个信号处理电路可以看作是高通滤波器和低通滤波器的组合，一个滤波器的输出是另外一个滤波器的输入，从系统响应的角度，认为整个信号处理电路的MTF是高通滤波器的MTF和低通滤波器的MTF的乘积:

上式是从普遍意义上对光电成像系统的信号处理电路MTF进行了分析，当针对具体的系统时，要分析其电路构成，求出其MTF值。

3.5 显示装置的MTF

显示装置的种类很多，其中最常用的是监视器是阴极射线管CRT，其传递函数如下［10］:

式中，σm为光斑尺寸参数，可以采用收缩光栅技术测出。

3.6 系统总的MTF

光电系统总的调制传递函数(MTF)是系统各个组成部分调制传递函数的乘积，根据上面的分析，可得系统总的MTF为:

根据上式可以建立基于MTF的光电成像的模型，分析输入和输出图像的关系，进行系统仿真实验。

4 非线性噪声影响分析

基于MTF光电成像系统模型的理论基础是假定光电成像系统是线性的。然而在实际中，光电成像系统各组成部分都不同程度的有非线性效应，为了提高模型的精度，常采用加入合理的噪声模型模拟非线性效应的作用。非线性效应在光电成像系统中主要表现在以下几个方面［11］:

(1)大气中气溶胶分布密度和湍流状态随机的非线性变化;

(2)光学系统透过率随入射光光谱成分的非线性变化;

(3)探测器量子效率随入射光非线性变化;

(4)信号处理电路中的非线性效应;

(5)显示装置随光强的非线性变化。

在实际模型的建立中，为了反映这种非线性效应对光电成像系统模型的影响，通过在MTF模型上叠加适当的噪声模型。通常采用叠加三维噪声模型的方法，三维噪声模型能够全面表征所有的噪声源特征，具有普遍意义。通过把噪声分为可以管理的数据集，使得复杂问题简单化，能够较好的反映光电成像系统的非线性效应对输出图像的影响［12］，三维噪声模型的数学表达式如下:

式中，σsys为系统总噪声，其他7种噪声含义如表1所示。

表1 三维噪声模型中的噪声分量描述

从表1可以看出，系统总的噪声是由7种产生机理不同的噪声组成，在具体的光电成像系统中并不是存在所有的噪声，可能是其中几种噪声占主导地位，这和系统所采用的成像技术有密切的关系［13］。

5 仿真分析

根据上面调制传递函数的计算方法和光电成像系统的使用要求及性能指标，在系统研制之前就可以建立其MTF模型进行仿真模型，以评价和改进光学成像系统，采用图1所示的仿真思路，再叠加合理的噪声，就可以建立光电系统的输入输出模型。

选择标准圆形标准靶板为输入图像进行模拟，采用Matlab编程将上述模型程序化，针对具体光电成像系统求得各组成部分的MTF，进而求得系统总的MTF，叠加合理的噪声模型，可得到系统的输入和输出的图像，如图3和图4所示。下面以前期设计的一个红外成像系统为例，对其进行仿真分析，评价其系统质量。

图3 光电成像系统的输入图像

图4 光电成像系统的输出图像

从上图可以看出输入图像经过光电成像系统以后，输出图像对比度和分辨率有所降低，并且变的有些模糊，但总体上对目标进行了良好的成像，能够满足发现和识别的要求。

6 结论

本文在分析了调制传递函数的基本理论之后，提出了建立基于MTF的光电成像系统的模型，通过分析光电成像系统中的各个环节的传递函数，最终计算得到了系统总的MTF，通过对输入和输出图像进行仿真分析，可以为光电系统的设计提供理论依据。

［1］ WANG Xuewei，LI Ke，WANG Shili．Research on modeling and simulation methods of infrared imaging system［J］．Computer＆Digital Engineering，2012，40(6):124－126．(in Chinese)王学伟，李珂，王世立．红外成像系统建模仿真方法研究［J］．计算机与数字工程，2012，40(6):124－126．

［2］ LNaiguang．Fourier optics［M］．Beijing:CHINA MACHINE PRESS，2006:144－163．(in Chinese)吕乃光．傅里叶光学［M］．北京:机械工业出版社，2006:144－163．

［3］ Ronald G Driggers，Melvin H Friedman，Jonathan Nichols．Introduction to infrared and electro-optical systems［M］．ARTECH HOUSE，1999:163－262．

［4］ WU Pengfei，FANG Shuai，XU Qingshan，et al．Restoration of blurred image based on atmospheric MTF［J］．Journal of Atmospheric and Environmental Optics，2011，6(3):196－202．(in Chinese)武鹏飞，方帅，徐青山，等．基于大气MTF的退化图像复原［J］．大气与环境光学学报．2011，6(3):196－202．

［5］ YAN Juncheng，WANG Defei，QI Wenzong．Research on the electro-optic performance of infrared detectors influenced by the atmosphere turbulence［J］．Laser＆Infrared，2009，39(2):162－165．(in Chinese)闫俊成．大气湍流对红外探测器光电性能影响的研究［J］．激光与红外，2009，39(2):162－165．

［6］ Gaskill，J，Linear Systems．Fourier transforms and optics［M］．New York:Wiley，1978:305－307．

［7］ GUO Yue，LIU Xiaopeng，YANG Hua．MTF analysis for CCD［J］．Spacecraft Recovery＆Remote Sensing，2004，25(3):25－28．(in Chinese)郭悦，刘晓鹏，杨桦．CCD的调制传递函(MTF)分析［J］．航天返回与遥感，2004，25(3):25－28．

［8］ REN Hang，ZHANG Tao．Effect of carrier diffusion on modulation transfer function of CCD［J］．Journal of Applied Optics，2009，30(2):257－262．(in Chinese)任航，张涛．载流子扩散对CCD调制传递函数的影响［J］．应用光学，2009，30(2):257－262．

［9］ HU Fangming．The technical research on modeling and performance evaluation of Electro-optical imaging system［D］．Xi'an:Xidian University，2005．(in Chinese)胡方明．光电成像系统建模及性能评估技术研究［D］．西安:西安电子科技大学，2005．

［10］Vollmerhausen，R．Impact of display modulation transfer function on the quality of sampled imagery［C］．SPIE Proceeding of Aerospace/Defense Sensing and Controls，Orlando FL，Apr．1996．

［11］LIU Huitong，WANG Qi，ZHENG Zhiwei，et al．Analysis and calculation of the nonlinear response in infrared focal plane arrays［J］．J．Infrared Millim．Waves，2001，20(4):253－258．(in Chinese)刘会通，王琪，郑志伟，张明，红外焦平面阵列非线性响应的分析和计算［J］．红外与毫米波学报，2001，20(4):253－258．

［12］Gerald C．Holst．Testing and evaluation of infrared imaging systems［M］．Second Editon．America:JCD Publishing and SPIE Optical Engineering Press，1998．171－249．

［13］ZHANG Zhenzhong，LI Anan．Physical effect modeling of electro-optical imaging system［J］．Journal of Xianyang Normal University，2011，26(2):27－31．(in Chinese)张振中．光电成像系统物理效应建模［J］．咸阳师范学院学报，2011，26(2):27－31．